Trắc nghiệm Bài toán liên quan đến tỉ lệ Toán 7 có đáp án
Trắc nghiệm Bài toán liên quan đến tỉ lệ
Tam giác \(ABC\) có trung tuyến \(AM = 12\,cm\) và trọng tâm \(G\). Độ dài đoạn \(AG\) là
-
A
\(4,5\,cm\)
-
B
\(3\,cm\)
-
C
\(6\,cm\)
-
D
\(8\,cm\)
Cho \(G\) là trọng tâm của tam giác đều. Chọn câu đúng.
-
A
\(GA = GB = GC\)
-
B
\(GA = GB > GC\)
-
C
\(GA < GB < GC\)
-
D
\(GA > GB > GC\)
Cho tam giác \(ABC\), các đường trung tuyến \(BD\) và \(CE\). Chọn câu đúng.
-
A
\(BD + CE < \dfrac{3}{2}BC\)
-
B
\(BD + CE > \dfrac{3}{2}BC\)
-
C
\(BD + CE = \dfrac{3}{2}BC\)
-
D
\(BD + CE = BC\)
Cho tam giác $MNP,$ hai đường trung tuyến $ME$ và $NF$ cắt nhau tại $O.$ Tính diện tích tam giác $MNP,$ biết diện tích tam giác $MNO$ là \(12c{m^2}\).
-
A
$18\,c{m^2}$
-
B
\(48\,c{m^2}\)
-
C
\(36\,c{m^2}\)
-
D
\(24\,c{m^2}\)
Chọn câu sai.
-
A
Trong một tam giác có ba đường trung tuyến
-
B
Các đường trung tuyến của tam giác cắt nhau tại một điểm.
-
C
Giao của ba đường trung tuyến của một tam giác gọi là trọng tâm của tam giác đó.
-
D
Một tam giác có hai trọng tâm
Điền số thích hợp vào chỗ chấm: “Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng … độ dài đường trung tuyến đi qua đỉnh ấy”
-
A
\(\dfrac{2}{3}\)
-
B
\(\dfrac{3}{2}\)
-
C
\(3\)
-
D
\(2\)
Tam giác \(ABC\) có trung tuyến \(AM = 9\,cm\) và trọng tâm \(G\). Độ dài đoạn \(AG\) là
-
A
\(4,5\,cm\)
-
B
\(3\,cm\)
-
C
\(6\,cm\)
-
D
\(4\,cm\)
Cho \(G\) là trọng tâm của tam giác đều. Chọn câu đúng.
-
A
\(GA = GB = GC\)
-
B
\(GA = GB > GC\)
-
C
\(GA < GB < GC\)
-
D
\(GA > GB > GC\)
Cho tam giác \(ABC\) có hai đường trung tuyến \(BD;CE\) sao cho \(BD = CE\). Khi đó tam giác \(ABC\)
-
A
Cân tại \(B.\)
-
B
Cân tại \(C.\)
-
C
Vuông tại \(A.\)
-
D
Cân tại \(A.\)
Cho tam giác $ABC$ có các đường trung tuyến \(BD\) và \(CE\) vuông góc với nhau. Tính độ dài cạnh \(BC\) biết \(BD = 9\,cm;\,CE = 12\,cm.\)
-
A
\(BC = 12\,cm.\)
-
B
\(BC = 6\,cm.\)
-
C
\(BC = 8\,cm.\)
-
D
\(BC = 10\,cm.\)
Cho tam giác \(ABC\), các đường trung tuyến \(BD\) và \(CE\). Chọn câu đúng.
-
A
\(BD + CE < \dfrac{3}{2}BC\)
-
B
\(BD + CE > \dfrac{3}{2}BC\)
-
C
\(BD + CE = \dfrac{3}{2}BC\)
-
D
\(BD + CE = BC\)
Cho tam giác \(ABC\), đường trung tuyến \(BD\). Trên tia đối của tia $DB$ lấy điểm \(E\) sao cho \(DE = DB.\) Gọi \(M,N\) theo thứ tự là trung điểm của \(BC;CE.\) Gọi \(I;K\) theo thứ tự là giao điểm của \(AM,AN\) với \(BE.\) Chọn câu đúng.
-
A
\(BI = IK > KE\)
-
B
\(BI > IK > KE\)
-
C
\(BI = IK = KE\)
-
D
\(BI < IK < KE\)
Cho tam giác $ABC$ vuông tại $A$ có $AB = 5cm,BC = 13cm$ . Ba đường trung tuyến $AM,BN,CE$ cắt nhau tại $O.$
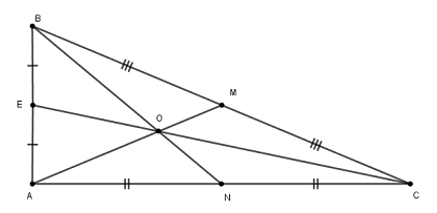
Độ dài trung tuyến $BN$ là :
-
A
$6cm\;$
-
B
\(\sqrt {61} \,cm\)
-
C
$12cm$
-
D
\(\sqrt {65} \,cm\)
Cho tam giác \(ABC\), đường trung tuyến \(BD\). Trên tia đối của tia $DB$ lấy điểm \(E\) sao cho \(DE = DB.\) Gọi \(M,N\) theo thứ tự là trung điểm của \(BC;CE.\) Gọi \(I;K\) theo thứ tự là giao điểm của \(AM,AN\) với \(BE.\) Chọn câu đúng.
-
A
\(BI = IK > KE\)
-
B
\(BI > IK > KE\)
-
C
\(BI = IK = KE\)
-
D
\(BI < IK < KE\)

















