Hoạt động 6 trang 78 Tài liệu dạy – học Toán 8 tập 2

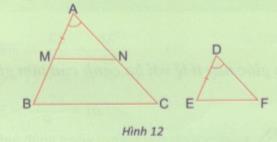
Đề bài

Cho tam giác ABC và tam giác DEF (hình 12) có : ${{DE} \over {AB}} = {{DF} \over {AC}};\widehat D = \widehat A\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)$

Hãy điền vào chỗ trống sau :

Trên tia AB, lấy điểm M sao cho AM = DE.

Qua M kẻ MN // BC ($N \in AC$ ).

Ta có : $\Delta AMN \sim \Delta .... \Rightarrow {{AM} \over {AB}} = {{AN} \over {....}}$

Vì AM = DE nên ${{DE} \over {AB}} = {{...} \over {AC}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)$

Từ (1), (2), suy ra AN = …

$\Delta AMN$ và $\Delta D{\rm{EF}}$ có AM = DE, $\widehat A = \widehat D$ (gt) và AN = DF (chứng minh trên), nên $\Delta AMN = \Delta DEF$ (c.g.c).

Suy ra : $\Delta ABC \sim \Delta ....$

Lời giải chi tiết

Cho tam giác ABC và tam giác DEF (hình 12) có : ${{DE} \over {AB}} = {{DF} \over {AC}};\widehat D = \widehat A\,\,\,\,\,\,\,(1)$

Trên tia AB, lấy điểm M sao cho AM = DE.

Qua M kẻ MN // BC ($N \in AC$).

Ta có : $\Delta AMN \sim \Delta ABC \Rightarrow {{AM} \over {AB}} = {{AN} \over {AC}}$

Vì AM = DE nên ${{DE} \over {AB}} = {{AN} \over {AC}}\,\,\,\,\,\,\,\,(2)$

Từ (1), (2), suy ra AN = DF

$\Delta AMN$ và $\Delta D{\rm{EF}}$ có AM = DE, $\widehat A = \widehat D$ (gt) và AN = DF (chứng minh trên)

Nên $\Delta AMN = \Delta DEF$ (c.g.c) $\Rightarrow \Delta ABC \sim \Delta DEF$

Loigiaihay.com