Chủ đề 4. Dòng điện, mạch điện SBT Vật lí 11 Cánh diềuSố electron dẫn trong 1 m3 ở dây dẫn điện kim loại vào cỡ Tổng hợp đề thi giữa kì 2 lớp 11 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
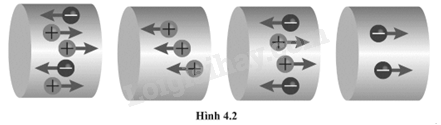
4.1 - 4.10 4.1. Số electron dẫn trong 1 m3 ở dây dẫn điện kim loại vào cỡ A. 1010. B. 1016. C. 1022. D. 1028. Phương pháp giải: Vận dụng kiến thức đã học về mật độ electron dẫn ở dây dẫn điện: \(n = {n_{ht}}.\frac{{{N_A}.D}}{M}\) Lời giải chi tiết: Chọn loại kim loại thường dùng cho dây dẫn điện là đồng (Cu) Mật độ electron dẫn trong 1 m3 ở dây dẫn điện bằng đồng là: \(n = {n_{ht}}.\frac{{{N_A}.D}}{M} = 2.\frac{{6,{{023.10}^{23}}.8960}}{{{{64.10}^{ - 3}}}} = 1,{7.10^{29}}{\rm{ e/}}{{\rm{m}}^3}\) Như vậy, số electron dẫn trong 1 m3 ở dây dẫn điện kim loại gần với đáp án 1028 nhất. Đáp án: D. 1028. 4.2. Tốc độ dịch chuyển có hướng của các electron trong một dây dẫn kim loại A. 1 cm/s. B. 10 cm/s. C. 104 m/s. D. 108 m/s. Phương pháp giải: Vận dụng kiến thức đã học về cường độ dòng điện trong dây dẫn: I = Snve Lời giải chi tiết: Dây dẫn bình thường có cỡ mm nên tiết diện S của dây điện có cỡ mm2. Cường độ dòng điện I bình thường cỡ khoảng 10 A. Một điện tích q có độ lớn cỡ 10-19 C. Tốc độ dịch chuyển có hướng của các electron trong một dây dẫn này vào khoảng: \(v = \frac{I}{{QnS}} = \frac{{10}}{{{{10}^{ - 19}}{{.10}^{28}}.{{\left( {{{10}^{ - 3}}} \right)}^2}}} = 0,01{\rm{ m/s = }}1{\rm{ cm/s}}\) Đáp án: A. 1 cm/s. 4.3. Xét các điện tích dương và âm đều dịch chuyển có hướng và theo phương ngang với cùng tốc độ ở bốn vùng dẫn điện khác nhau (Hình 4.2). Gọi I1 là cường độ dòng điện do các điện tích dịch chuyển tạo ra trong vùng đầu tiên bên trái, I2, I3, I4 là cường độ dòng điện tương ứng trong các vùng tiếp theo (tính từ trái sang phải). Độ lớn của các cường độ dòng điện này từ lớn nhất đến nhỏ nhất được xếp theo thứ tự nào sau đây?
A. I2, I1, I3, I4.
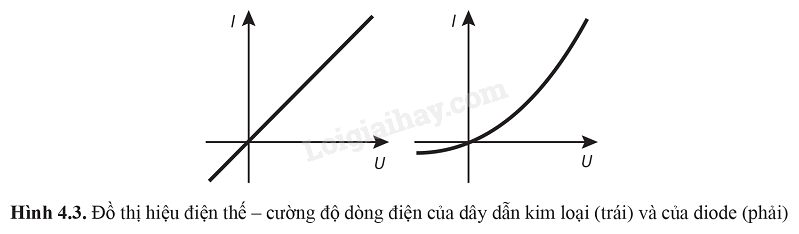
B. I1, I3, I2, I4. C. I3, I1, I4, I2. D. I4, I2, I3, I1. Phương pháp giải: Vận dụng kiến thức đã học về cường độ dòng điện trong dây dẫn: I = Snve Lời giải chi tiết: Đặt: \(i = veS\) \( \Rightarrow I = venS = i{n_e}\) \(\begin{array}{l}{I_1} = in = \left( { + 2 + 3} \right)i = 5i\\{I_2} = in = \left( { - 3} \right)i = - 3i\\{I_3} = in = \left( { + 2 + 2} \right)i = 4i\\{I_4} = in = \left( { - 2} \right)i = - 2i\end{array}\) Xét về độ lớn, cường độ dòng điện trong các vùng được xếp theo thứ tự: \({I_1} > {I_3} > {I_2} > {I_4}\) Đáp án: B. I1, I3, I2, I4. 4.4. Giả sử một dây dẫn điện bằng đồng có tiết diện nhỏ dần dọc theo dây từ đầu này sang đầu kia của dây. Trong dây có dòng điện với cường độ I chạy qua. Tốc độ dịch chuyển có hướng của electron thay đổi như thế nào dọc theo dây? A. Giảm dần khi tiết diện dây nhỏ dần. B. Tăng dần khi tiết diện dây nhỏ dần. C. Không thay đổi. D. Không đủ thông tin để trả lời. Phương pháp giải: Vận dụng kiến thức đã học về cường độ dòng điện trong dây dẫn: I = Snve Lời giải chi tiết: Đáp án: B. Tăng dần khi tiết diện dây nhỏ dần. 4.5. Tính cường độ dòng điện qua dây dẫn điện nếu 2,85.1020 electron đi qua tiết Phương pháp giải: Áp dụng kiến thức về cường độ dòng điện: \(I = \frac{{\Delta q}}{{\Delta t}}\) Lời giải chi tiết: Cường độ dòng điện qua dây dẫn điện là: \(I = \frac{{\Delta q}}{{\Delta t}} = \frac{{2,{{85.10}^{20}}.1,{{6.10}^{ - 19}}}}{{60}} = 0,76{\rm{ A}}\) 4.6. Cường độ dòng điện 0,60 A chạy qua sợi đốt của một bóng đèn. Nếu để bóng đèn sáng trong 8,0 phút thì có bao nhiêu electron di chuyển qua bóng đèn? Biết điện tích của electron là e = –1,6.10-19 C. Phương pháp giải: Vận dụng kiến thức đã học về cường độ dòng điện: \(I = \frac{{\Delta q}}{{\Delta t}}\) Lời giải chi tiết: Số electron đi qua bóng đèn trong 8 phút là: \(n = \frac{{\Delta q}}{e} = \frac{{I\Delta t}}{e} = \frac{{0,6.8.60}}{{1,{{6.10}^{ - 19}}}} = 1,{8.10^{21}}{\rm{ e}}\) 4.7. Tính cường độ dòng điện chạy trong dây đồng có tiết diện 7,5.10–7 m2 để tốc độ dịch chuyển có hướng của electron dẫn là 5,00.10-4 m/s. Phương pháp giải: Vận dụng kiến thức đã học về cường độ dòng điện: - Cường độ dòng điện trong dây dẫn: I = Snve - Mật độ electron dẫn ở dây dẫn điện: \(n = {n_{ht}}.\frac{{{N_A}.D}}{M}\) Lời giải chi tiết: Mật độ electron dẫn trong 1 m3 dây đồng là: \(\begin{array}{l}n = {n_{ht}}.\frac{{{N_A}.D}}{M} = 2.\frac{{6,{{023.10}^{23}}.8960}}{{{{64.10}^{ - 3}}}} = 1,{7.10^{29}}{\rm{ e/}}{{\rm{m}}^2}\\\end{array}\) Cường độ dòng điện của dây đồng là: \(I = venS = {5.10^{ - 4}}.1,{6.10^{ - 19}}.1,{7.10^{29}}.7,{5.10^{--7}} = 10,2{\rm{ A}}\) 4.8. Trong một dây dẫn điện có dòng điện với cường độ 80,0 mA. Phương pháp giải: Vận dụng kiến thức đã học về electron đi qua tiết diện thẳng của dây: - Số hạt electron đi qua tiết diện thẳng của dây: \(n = \frac{{\Delta q}}{e}\) - Các electron, ion âm, hạt mang điện âm chuyển động ngược chiều dòng điện; Các ion dương, hạt mang điện dương chuyển động cùng chiều dòng điện. Lời giải chi tiết: a) Số electron đi qua dây trong 10 phút là: \({n_e} = \frac{{\Delta q}}{e} = \frac{{I\Delta t}}{e} = \frac{{{{80.10}^{ - 3}}.10.60}}{{1,{{6.10}^{ - 19}}}} = {3.10^{20}}{\rm{ e}}\) b) Các electron chuyển động ngược chiều dòng điện. 4.9. Trong mô hình nguyên tử hyđro của Bohr, một electron ở mức năng lượng thấp nhất chuyển động với tốc độ bằng 2,19.106 m/s theo một quỹ đạo tròn có bán kính 5,29.10–11 m. Tính cường độ dòng điện tương ứng với chuyển động này của electron. Phương pháp giải: Vận dụng kiến thức đã học về chuyển động tròn đều và cường độ dòng điện: - Chuyển động tròn, chu kì \(T = \frac{{2\pi r}}{v}\) - Cường độ dòng điện: \(I = \frac{{\Delta q}}{{\Delta t}}\) Lời giải chi tiết: Electron chuyển động theo quỹ đạo tròn với chu kì \(T = \frac{{2\pi r}}{v}\) Cường độ dòng điện tương ứng với chuyển động này là: \(I = \frac{{\Delta q}}{{\Delta t}} = \frac{{\left| e \right|}}{T} = \frac{{\left| e \right|.v}}{{2\pi r}} = \frac{{1,{{6.10}^{ - 19}}.2,{{19.10}^6}}}{{2\pi .5,{{29.10}^{--11}}}} = 1,{05.10^{ - 3}}{\rm{ A}} = 1,05{\rm{ mA}}\) 4.10. Tính cường độ dòng điện khi một điện tích 240 C chạy qua một tiết diện thẳng của dây dẫn trong thời gian 2 phút. Phương pháp giải: Vận dụng kiến thức đã học về cường độ dòng điện: \(I = \frac{{\Delta q}}{{\Delta t}}\) Lời giải chi tiết: Cường độ dòng điện qua dây dẫn là: \(I = \frac{{\Delta q}}{{\Delta t}} = \frac{{240}}{{2.60}} = 2{\rm{ A}}\) 4.11 - 4.15 4.11. Trong một thí nghiệm mạ bạc, cần có điện tích 9,65.104 C để lắng đọng một Phương pháp giải: Vận dụng kiến thức đã học về cường độ dòng điện: \(I = \frac{{\Delta q}}{{\Delta t}}\) Lời giải chi tiết: Thời gian để khối bạc này lắng đọng là: \(\Delta t = \frac{{\Delta q}}{I} = \frac{{9,{{65.10}^4}}}{{0,2}} = 4,{8.10^5}{\rm{ s}}\) 4.12. Cường độ dòng điện trong một dây dẫn là 200 mA. Tính: Phương pháp giải: Vận dụng kiến thức đã học về: - Cường độ dòng điện: \(I = \frac{{\Delta q}}{{\Delta t}}\) - Số hạt electron đi qua tiết diện thẳng của dây: \(n = \frac{{\Delta q}}{e}\) Lời giải chi tiết: a) Lượng điện tích đi qua tiết diện thẳng của dây trong 5 phút là: \(\Delta q = I\Delta t = {200.10^{ - 3}}.5.60 = 60{\rm{ C}}\) b) Số hạt electron cần để mang điện tích này là: \(n = \frac{{\Delta q}}{e} = \frac{{60}}{{1,{{6.10}^{ - 19}}}} = 3,{75.10^{20}}{\rm{ e}}\) 4.13. Một dây đồng có 8,5.1028 electron tự do trong một mét khối. Dây có tiết diện thẳng (diện tích mặt cắt ngang) là 1,2 mm2 và trong dây có cường độ dòng điện 2,0 A. Tính tốc độ chuyển động có hướng của các electron. Phương pháp giải: Vận dụng kiến thức đã học về cường độ dòng điện trong dây dẫn: I = Snve Lời giải chi tiết: Tốc độ chuyển động có hướng của các electron là: \(v = \frac{I}{{enS}} = \frac{2}{{1,{{6.10}^{ - 19}}.8,{{5.10}^{28}}.1,{{2.10}^{--6}}}} = 1,{2.10^{ - 4}}{\rm{ m/s}}\) 4.14. Tốc độ dịch chuyển có hướng của các eclectron dẫn trong một dây kim loại là 6,5.10–4 m/s khi cường độ dòng điện là 0,80 A. Đường kính của dây là 0,50 mm. Tính số electron dẫn trên một đơn vị thể tích dây dẫn. Phương pháp giải: Vận dụng kiến thức đã học về cường độ dòng điện trong dây dẫn: I = Snve Lời giải chi tiết: Mật độ electron dẫn trong dây kim loại là: \(n = \frac{I}{{veS}} = \frac{{0,8}}{{\pi .6,{{5.10}^{--4}}.1,{{6.10}^{ - 19}}.{{\left( {0,{{25.10}^{--3}}} \right)}^2}}} = 3,{9.10^{28}}{\rm{ e/}}{{\rm{m}}^3}\) 4.15. Trong một dây dẫn điện bằng đồng có cường độ dòng điện 10,0 A. Giả sử số electron tự do trong kim loại đồng là do mỗi nguyên tử đồng đóng góp một electron. Biết dây đồng có tiết diện 3,00.10–6 m2; khối lượng riêng của đồng là 8,92 g/cm3; khối lượng mol nguyên tử đồng là 63,5 g/mol; số Avogadro là 6,02.1023 nguyên tử/mol. Phương pháp giải: Vận dụng kiến thức đã học về: - Mật độ electron dẫn ở dây dẫn điện: \(n = {n_{ht}}.\frac{{{N_A}.D}}{M}\) - Cường độ dòng điện trong dây dẫn: I = Snve Lời giải chi tiết: Mật độ electron dẫn trong dây đồng này là: \(n = {n_{ht}}.\frac{{{N_A}.D}}{M} = 1.\frac{{6,{{02.10}^{23}}.8920}}{{63,{{5.10}^{ - 3}}}} = 8,{46.10^{28}}{\rm{ e/}}{{\rm{m}}^3}\) Tốc độ dịch chuyển có hướng của các electron trong dây đồng này là: \(v = \frac{I}{{enS}} = \frac{{10}}{{1,{{6.10}^{ - 19}}.8,{{46.10}^{28}}{{.3.10}^{ - 6}}}} = 2,{46.10^{ - 4}}{\rm{ m/s}}\) 4.16 - 4.28 4.16. Đặt hiệu điện thế 6 V vào hai đầu điện trở 3 Ω. Cường độ dòng điện chạy qua điện trở là A. 0,5 A. B. 6 A. C. 2 A. D. 3 A. Phương pháp giải: Vận dụng kiến thức đã học về cường độ dòng điện qua một vật dẫn kim loại: \(I = \frac{U}{R}\) Lời giải chi tiết: Cường độ dòng điện chạy qua điện trở là: \(I = \frac{U}{R} = \frac{6}{3} = 2{\rm{ A}}\) Đáp án: C. 2 A. 4.17. Đặt một hiệu điện thế 12 V vào giữa hai đầu một điện trở 4,0 Ω thì lượng điện tích chạy qua điện trở trong mỗi giây là A. 3 C. B. 4 C. C. 12 C. D. 48 C. Phương pháp giải: Vận dụng kiến thức đã học về cường độ dòng điện: - Cường độ dòng điện: \(I = \frac{{\Delta q}}{{\Delta t}}\) - Cường độ dòng điện qua một vật dẫn kim loại: \(I = \frac{U}{R}\) Lời giải chi tiết: Lượng điện tích chạy qua điện trở trong mỗi giây là: \(\Delta q = I\Delta t = \frac{U}{R}\Delta t = \frac{{12}}{4}.1 = 3{\rm{ C}}\) Đáp án: A. 3 C. 4.18. Ở Hình 4.3, khi hiệu điện thế U tăng, phát biểu nào sau đây đúng? A. Điện trở của diode tăng. B. Điện trở của dây kim loại giảm. C. Điện trở của diode giảm. D. Điện trở của dây kim loại tăng.
Phương pháp giải: Vận dụng kiến thức đã học về điện trở và cách đọc đồ thị. - Điện trở: \(R = \frac{U}{I}\) Lời giải chi tiết: Đáp án: C. Điện trở của diode giảm. 4.19. Một dây dẫn kim loại có điện trở R được cắt thành ba đoạn bằng nhau rồi tết lại với nhau để tạo thành một dây dẫn mới có chiều dài bằng 1/3 chiều dài ban đầu. Điện trở của dây mới này có giá trị là A. 3R. B. R/9. C. R/3. D. 9R. Phương pháp giải: Vận dụng kiến thức đã học về điện trở trong dây dẫn: \(R = \rho \frac{l}{S}\) Lời giải chi tiết: Ta có: \(l' = \frac{1}{3}l;{\rm{ }}S' = 3S{\rm{; }}R = \rho \frac{l}{S}\) \( \Rightarrow R' = \rho \frac{{l'}}{{S'}} = \rho \frac{l}{{3.3S}} = \frac{R}{9}\) Đáp án: B. R/9. 4.20. Cho mạch điện (Hình 4.4), các điện trở R đều bằng nhau. Điện trở tương đương giữa M và N là A. R/2. B. R. C. 2R. D. 4R.
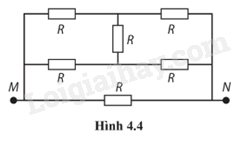
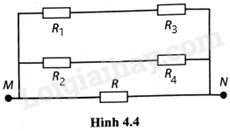
Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Mạch cầu: khi \(\frac{{{R_1}}}{{{R_3}}} = \frac{{{R_2}}}{{{R_4}}}\) thì sơ đồ mạch được vẽ lại: (R1ntR2)//(R3ntE4)//R - Điện trở song song: \(\frac{1}{R} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + ... + \frac{1}{{{R_n}}}\) - Điện trở nối tiếp: R = R1 + R2 + … + Rn Lời giải chi tiết:
Vì \(\frac{{{R_1}}}{{{R_3}}} = \frac{{{R_2}}}{{{R_4}}} = 1\) nên mạch điện được vẽ lại như hình bên. Sơ đồ mạch: (R1ntR2)//(R3ntE4)//R \(\begin{array}{l}\frac{1}{{{R_{MN}}}} = \frac{1}{{{R_{13}}}} + \frac{1}{{{R_{24}}}} + \frac{1}{R} = \frac{1}{{{R_1} + {R_3}}} + \frac{1}{{{R_2} + {R_4}}} + \frac{1}{R} = \frac{1}{{R + R}} + \frac{1}{{R + R}} + \frac{1}{R} = \frac{2}{R}\\ \Rightarrow {R_{MN}} = \frac{R}{2}\end{array}\) 4.21. Cường độ dòng điện đi qua một vật dẫn là 6,3 A khi hiệu điện thế giữa hai đầu vật dẫn là 12 V. Tính điện trở của vật dẫn. Phương pháp giải: Vận dụng kiến thức đã học về điện trở của vật dẫn: \(R = \frac{U}{I}\) Lời giải chi tiết: Điện trở của vật dẫn là: \(R = \frac{U}{I} = \frac{{12}}{{6,3}} = 1,9{\rm{ }}\Omega \) 4.22. Đồ thị I – U của một vật dẫn được biểu diễn ở Hình 4.5.
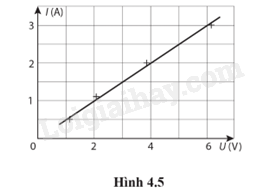
Phương pháp giải: Vận dụng kiến thức đã học về: - Định luật Ohm: cường độ dòng điện đi qua 2 điểm của một vật dẫn điện luôn có tỷ lệ thuận với hiệu điện thế đi qua 2 điểm đó, và cường độ dòng điện tỷ lệ nghịch với điện trở của dây dẫn. - Điện trở của vật dẫn: \(R = \frac{U}{I}\) Lời giải chi tiết: a) Từ đồ thị có thể suy ra định luật Ohm. b) Điện trở của vật dẫn là: \(R = \frac{U}{I} = \frac{2}{1} = 2{\rm{ }}\Omega \) 4.23. Cho mạch điện (Hình 4.6). Hiệu điện thế U = 12 V, điện trở các dây nối không đáng kể.
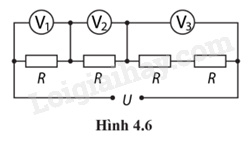
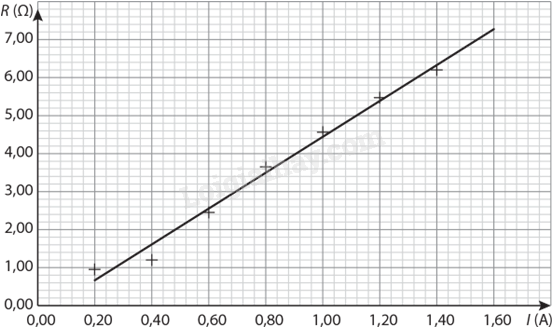
Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Điện trở nối tiếp: R = R1 + R2 + … + Rn; U = U1 + U2 + … + Un; I = I1 = I2 = … = In. - Điện trở của vật dẫn: \(R = \frac{U}{I}\) Lời giải chi tiết: Điện trở tương đương của mạch điện này là: \({R_{td}} = R + R + R + R = 4R\) Cường độ dòng điện trong mạch là: \(I = \frac{U}{{{R_{td}}}} = \frac{{12}}{{4{\rm{R}}}} = \frac{3}{R}{\rm{ A}}\) Số chỉ vôn kế 1 và 2: \({V_1} = IR = {V_2} = \frac{3}{R}R = 3{\rm{ V}}\) Số chỉ vôn kế 3: \({V_3} = I\left( {R + R} \right) = \frac{3}{R}.2R = 6{\rm{ V}}\) 4.24. Khi hiệu điện thế giữa hai đầu LED là 2,0 V thì cường độ dòng điện đi qua nó là 20 mA. Tính điện trở của LED. Phương pháp giải: Vận dụng kiến thức đã học về điện trở của vật dẫn: \(R = \frac{U}{I}\) Lời giải chi tiết: Điện trở của LED là: \(R = \frac{U}{I} = \frac{2}{{{{20.10}^{ - 3}}}} = 100{\rm{ }}\Omega \) 4.25. Bảng sau đây là các giá trị của cường độ dòng điện I qua một điện trở tương
a) Tính giá trị của điện trở ứng với mỗi giá trị cường độ dòng điện và hiệu điện thế. Phương pháp giải: Vận dụng kiến thức đã học về điện trở của vật dẫn: \(R = \frac{U}{I}\) Lời giải chi tiết: a)
b)
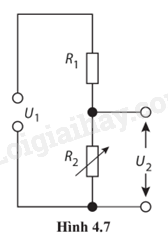
4.26. Cho mạch điện (Hình 4.7). U1 = 10 V; R1 = 10 Ω. Khi biến trở R2 thay đổi giá trị từ 0 V đến 40 V, xác định khoảng giá trị của hiệu điện thế U2.
Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Điện trở của vật dẫn: \(R = \frac{U}{I}\) - Điện trở nối tiếp: R = R1 + R2 + … + Rn; U = U1 + U2 + … + Un; I = I1 = I2 = … = In. Lời giải chi tiết: Khi R2 = 0; U2 = 0 Khi R2 = 40 Ω; \(\begin{array}{l}I = \frac{U}{R} = \frac{{{U_1}}}{{{R_1} + {R_2}}} = \frac{{10}}{{10 + 40}} = 0,2{\rm{ A; }}\\{U_2} = IR = 0,2.40 = 8{\rm{ V}}\end{array}\) 4.27. Khi hiệu điện thế giữa hai đầu của một vật dẫn là 2,00 V, cường độ dòng điện qua nó là 10,0 mA. Khi hiệu điện thế là 8,00 V, cường độ dòng điện là 60,0 mA. Phương pháp giải: Vận dụng kiến thức đã học về: - Định luật Ohm: cường độ dòng điện đi qua 2 điểm của một vật dẫn điện luôn có tỷ lệ thuận với hiệu điện thế đi qua 2 điểm đó, và cường độ dòng điện tỷ lệ nghịch với điện trở của dây dẫn. - Điện trở của vật dẫn: \(R = \frac{U}{I}\) Lời giải chi tiết: a) Điện trở của vật dẫn: Khi U = 2 V ; \(R = \frac{U}{I} = \frac{2}{{{{10.10}^{ - 3}}}} = 200{\rm{ }}\Omega {\rm{ }}\) Khi U = 8 V ; \(R = \frac{U}{I} = \frac{8}{{{{60.10}^{ - 3}}}} = 133{\rm{ }}\Omega {\rm{ }}\) b) Vì điện trở của vật dẫn thay đổi khi thay đổi cường độ dòng điện và hiệu điện thế nên vật dẫn này không tuân theo định luật Ohm.
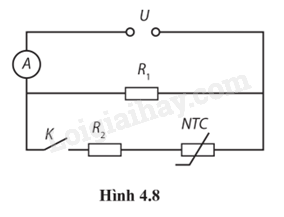
4.28. Cho mạch điện (Hình 4.8). NTC là điện trở nhiệt ngược. R1 = 5,0 Ω; R2 = 6,4 Ω. Bỏ qua điện trở của ampe kế và dây nối.
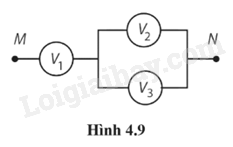
Khi ngắt công tắc K, ampe kế A chỉ 0,48 A. Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Định luật Ohm: cường độ dòng điện đi qua 2 điểm của một vật dẫn điện luôn có tỷ lệ thuận với hiệu điện thế đi qua 2 điểm đó, và cường độ dòng điện tỷ lệ nghịch với điện trở của dây dẫn. - Điện trở của vật dẫn: \(R = \frac{U}{I}\) - Điện trở song song: \(\frac{1}{R} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + ... + \frac{1}{{{R_n}}}\); I = I1 + I2 + … + In ; U = U1 = U2 = … = Un - Điện trở nối tiếp: R = R1 + R2 + … + Rn; U = U1 + U2 + … + Un; I = I1 = I2 = … = In - Khi tăng nhiệt độ của điện trở nhiệt, điện trở của điện trở nhiệt giảm. Lời giải chi tiết: a) Hiệu điện thế \(U = I{R_1} = 0,48.5 = 2,4{\rm{ V}}\) b) Khi đóng công tắc K. Điện trở tương đương của mạch là: \({R_b} = \frac{U}{I} = \frac{{2,4}}{{0,72}} = 3,3{\rm{ }}\Omega {\rm{ }}\) Mà \(\frac{1}{{{R_b}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_{2NTC}}}}\) \(\begin{array}{l}\frac{1}{{{R_b}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_{2NTC}}}}\\ \Rightarrow \frac{1}{{{R_{2NTC}}}} = \frac{1}{{{R_b}}} - \frac{1}{{{R_1}}} = \frac{1}{{3,3}} - \frac{1}{5} = \frac{1}{{10}}\\ \Rightarrow {R_{2NTC}} = 10{\rm{ }}\Omega \\{R_{2NTC}} = {R_2} + {R_{NTC}}\\ \Rightarrow {R_{NTC}} = {R_{2NTC}} - {R_2} = 10 - 6,4 = 3,6{\rm{ }}\Omega \end{array}\) Vậy điện trở của điện trở nhiệt là \({R_{NTC}} = 3,6{\rm{ }}\Omega \) c) Điện trở của điện trở nhiệt giảm nên điện trở toàn mạch giảm và số chỉ của ampe kế tăng. 4.29 - 4.38 4.29. Nối điện trở R với hai cực của một pin để có dòng điện chạy qua R. Hiệu điện thế giữa hai cực của pin là 1,6 V khi R = 4,0 Ω và là 1,8 V khi R = 9,0 Ω. Suất điện động và điện trở trong của pin có giá trị lần lượt là A. 1 V và 1 Ω. B. 2 V và 1 Ω. C. 2 V và 2 Ω. D. 2,5 V và 0,50 Ω. Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Điện trở của vật dẫn: \(R = \frac{U}{I}\) - Khi mạch kín, hiệu điện thế: U = E – Ir Lời giải chi tiết: \(\begin{array}{l}{I_1} = {U_1}{R_1} = \frac{{1,6}}{4} = 0,4{\rm{ A}}\\ \Rightarrow \xi = {I_1}r + {U_1} \Rightarrow \xi = 0,4r + 1,6{\rm{ }}\left( 1 \right)\\{I_2} = {U_2}{R_2} = \frac{{1,8}}{9} = 0,2{\rm{ A}}\\ \Rightarrow \xi = {I_2}r + {U_2} \Rightarrow \xi = 0,2r + 1,8{\rm{ }}\left( 2 \right)\end{array}\) Từ (1) và (2) \( \Rightarrow \xi = 2{\rm{ V; }}r = 1{\rm{ }}\Omega \) Đáp án: B. 2 V và 1 Ω. 4.30. Ở Hình 4.9, các vôn kế V1, V2, V3 có điện trở lần lượt là R, 1,5R và 3R. Đặt vào hai điểm M và N một hiệu điện thế thì số chỉ của các vôn kế tương ứng là U1, U2, U3. Hệ thức nào sau đây là đúng?
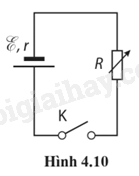
A. U1 = U2 = U3. B. U1 ≠ U2 = U3. C. U1 = U2 ≠ U3. D. U2 ≠ U1 = U3. Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Điện trở song song: \(\frac{1}{R} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + ... + \frac{1}{{{R_n}}}\); I = I1 + I2 + … + In ; U = U1 = U2 = … = Un - Điện trở nối tiếp: R = R1 + R2 + … + Rn; U = U1 + U2 + … + Un; I = I1 = I2 = … = In Lời giải chi tiết: Mạch điện có dạng: V1 nt (V2 // V3) => U1 ≠ U2 = U3. Đáp án: B. U1 ≠ U2 = U3. 4.31. Một bóng đèn điện được thiết kế để sáng đúng công suất định mức P0 khi hiệu điện thế giữa hai đầu đèn là U0. Nếu hiệu điện thế là U với U < U0, đèn sẽ sáng với công suất là A. \(P = \frac{{{U_0}}}{U}{P_0}.\) B. \(P = \frac{U}{{{U_0}}}{P_0}.\) C. \(P = {\left( {\frac{{{U_0}}}{U}} \right)^2}{P_0}.\) D. \(P = {\left( {\frac{U}{{{U_0}}}} \right)^2}{P_0}.\) Phương pháp giải: Vận dụng kiến thức đã học về công suất: - Công suất định mức là công suất khi đèn sáng bình thường: \({P_0} = \frac{{U_0^2}}{R}\) - Công suất tiêu thụ năng lượng điện của đoạn mạch: \(P = \frac{A}{t} = UI = \frac{{{U^2}}}{R}\) Lời giải chi tiết: Ta có: \({P_0} = \frac{{U_0^2}}{R};P = \frac{{{U^2}}}{R}\) Mà R không đổi. \( \Rightarrow P = {\left( {\frac{U}{{{U_0}}}} \right)^2}{P_0}\) Đáp án: D. \(P = {\left( {\frac{U}{{{U_0}}}} \right)^2}{P_0}.\) 4.32. Hai vật dẫn được nối với cùng một hiệu điện thế. Vật A có điện trở gấp đôi điện trở vật B. Tỉ số công suất tiêu thụ điện của vật A và của vật B là A. 2. B. 1/2. C. 1/4. D. 4. Phương pháp giải: Vận dụng kiến thức đã học về công suất tiêu thụ điện của điện trở \(P = {I^2}R\) Lời giải chi tiết: Công suất tiêu thụ điện \(P = {I^2}R\) \(\begin{array}{l}{R_A} = 2{{\rm{R}}_B}\\ \Rightarrow {P_A} = 2{P_B}\end{array}\) Đáp án: A. 2. 4.33. Mạch điện (Hình 4.10) có mạch ngoài là biến trở R. Đóng khoá K, thay đổi R để công suất ở mạch ngoài cực đại. Giá trị của biến trở và công suất cực đại lúc đó là
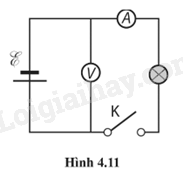
A. \(2r;{\rm{ }}\frac{{{E^2}}}{{2r}}.\) B. \(r;{\rm{ }}\frac{{{E^2}}}{{4r}}.\) C. \(r;{\rm{ }}\frac{{{E^2}}}{{2r}}.\) D. \(4r;{\rm{ }}\frac{{{E^2}}}{r}.\) Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Điện trở của vật dẫn: \(R = \frac{U}{I}\) - Điện trở trong của nguồn: \(r = \frac{{E - U}}{I}\) - Bất đẳng thức Cosy: \({a^2} + {b^2} \ge 2ab\) Dấu “=” xảy ra khi a = b Lời giải chi tiết: Công suất tiêu thụ của mạch ngoài: \(P = {I^2}R = {\left( {\frac{E}{{R + r}}} \right)^2}.R = \frac{{{E^2}}}{{{{\left( {\sqrt R + \frac{r}{{\sqrt R }}} \right)}^2}}}\) Áp dụng bất đẳng thức Cosy: \(\sqrt R + \frac{r}{{\sqrt R }} \ge 2\sqrt r \) Dấu “=” xảy ra khi R = r => Công suất cực đại lúc đó là \({P_{ma{\rm{x}}}} = \frac{{{E^2}}}{{4r}}\) Đáp án: B. \(r;{\rm{ }}\frac{{{E^2}}}{{4r}}.\) 4.34. Một ampe kế và một vôn kế được mắc nối tiếp với một pin. Khi đó, số chỉ của chúng lần lượt là I và U. Giữ nguyên các thành phần của mạch, mắc một điện trở R song song với vôn kế. Phát biểu nào sau đây là đúng? A. I và U đều tăng. B. I và U đều giảm. C. I sẽ giảm, U sẽ tăng. D. I sẽ tăng, U sẽ giảm. Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Điện trở song song: \(\frac{1}{R} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + ... + \frac{1}{{{R_n}}}\); I = I1 + I2 + … + In ; U = U1 = U2 = … = Un - Điện trở nối tiếp: R = R1 + R2 + … + Rn; U = U1 + U2 + … + Un; I = I1 = I2 = … = In Lời giải chi tiết: Mắc thêm điện trở song song vào mạch làm điện trở tương đương của mạch giảm. Mà \({R_b} = \frac{U}{I}\) Nên khi lắp thêm điện trở R thì I sẽ tăng, U sẽ giảm Đáp án: D. I sẽ tăng, U sẽ giảm. 4.35. Một acquy được dùng để cấp điện cho bóng đèn pin và đèn đang sáng. Nêu sự chuyển hoá năng lượng xảy ra trong Phương pháp giải: Vận dụng kiến thức về acquy và bóng đèn: - Acquy là một nguồn điện thứ cấp, hoạt động dựa trên quá trình chuyển đổi hóa năng thành điện năng. Ắc quy tạo ra và duy trì hiệu điện thế giữa hai đầu mạch điện. Có tác dụng tích trữ và cấp điện cho các thiết bị sử dụng điện. - Bóng đèn đang sáng, năng lượng điện chuyển thành năng lượng nhiệt và năng lượng ánh sáng. Lời giải chi tiết: a) Năng lượng hoá học chuyển thành năng lượng điện b) Năng lượng điện chuyển thành năng lượng nhiệt và năng lượng ánh sáng. 4.36. Cho mạch điện (Hình 4.11). Khi ngắt công tắc, vôn kế chỉ 13 V, khi đóng công tắc vôn kế chỉ 12 V và ampe kế chỉ 4,0 A. Tìm:
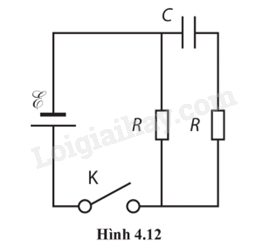
Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Khi mạch kín, hiệu điện thế: U = E – Ir - Khi mạch hở (ngắt công tắc): UR = 0; E = U - Điện trở trong của nguồn: \(r = \frac{{E - U}}{I}\) Lời giải chi tiết: a) Suất điện động của nguồn điện là số chỉ của vôn kế khi ngắt công tắc: E = 13 V b) Độ giảm điện thế trên điện trở trong khi đóng công tắc: E – U = 13 – 12 = 1 V c) Điện trở trong của nguồn điện: \(r = \frac{{E - U}}{I} = \frac{1}{4} = 0,25{\rm{ }}\Omega \) 4.37. Ba pin giống hệt nhau, mỗi pin có suất điện động 1,5 V, được mắc nối tiếp với bóng đèn có điện trở 15 Ω. Cường độ dòng điện trong mạch là 0,27 A. Tính điện trở trong của mỗi pin. Phương pháp giải: Vận dụng kiến thức đã học về nguồn điện: - Điện trở trong của nguồn: \({r_b} = \frac{{{E_b} - U}}{I} = \frac{{{E_b}}}{I} - R\) - Nguồn điện mắc nối tiếp: r = r1 + r2 + … + rn; E = E1 + E2 + … + En Lời giải chi tiết: Suất điện động của nguồn điện là: E = 3Ep = 3.1,5 = 4,5 V. Điện trở trong của nguồn điện là: \(r = \frac{E}{I} - R = \frac{{4,5}}{{0,27}} - 15 = 1,67{\rm{ }}\Omega \) Điện trở trong của mỗi pin là: \({r_p} = \frac{r}{3} = \frac{{1,67}}{3} = 0,56{\rm{ }}\Omega \) 4.38. Một pin có suất điện động là 1,5 V và điện trở trong là 0,50 Ω. Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Khi mạch kín, hiệu điện thế: U = E – Ir; U = IR - Công suất tiêu thụ của mạch ngoài: \(P = {I^2}R\) - Bất đẳng thức Cosy: \({a^2} + {b^2} \ge 2ab\) Dấu “=” xảy ra khi a = b Lời giải chi tiết: a) Cường độ dòng điện tối đa pin có thể cung cấp là: \(I = \frac{E}{r} = \frac{{1,5}}{{0,5}} = 3{\rm{ A}}\) Khi điện trở mạch ngoài bằng 0 thì pin có thể cung cấp dòng điện tối đa. b) Chọn mạch kín có một nguồn là pin E với điện trở trong r và một điện trở R cường độ dòng điện I chạy trong mạch. Công suất mà nguồn phát ra là công suất tiêu thụ của mạch ngoài: \(P = {I^2}R = \frac{{{E^2}}}{{{{\left( {R + r} \right)}^2}}}.R = \frac{{{E^2}}}{{{{\left( {\sqrt R + \frac{r}{{\sqrt R }}} \right)}^2}}}\) Áp dụng bất đẳng thức Cosi: \(\sqrt R + \frac{r}{{\sqrt R }} \ge 2\sqrt r \) Dấu “=” xảy ra khi R = r \( \Rightarrow {P_{\max }} = \frac{{{E^2}}}{{4r}} = \frac{{1,{5^2}}}{{4.0,5}} = 1,1{\rm{ W}}\) Công suất tối đa mà pin có thể cung cấp cho mạch ngoài là 1,1 W khi điện trở ngoài bằng điện trở trong. 4.39 - 4.48 4.39. Một nguồn 9,00 V cung cấp dòng điện 1,34 A cho bóng đèn pin trong 2 phút. Tính: Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Cường độ dòng điện: \(I = \frac{{\Delta q}}{{\Delta t}}\) - Số hạt electron đi qua đèn: \(n = \frac{{\Delta q}}{e}\) - Năng lượng mà nguồn cung cấp cho đèn: A = EIt Lời giải chi tiết: a) Điện tích đi qua đèn là: \(q = It = 1,34.2.60 = 161{\rm{ C}}\) b) Số electron chuyển qua đèn là : \(n = \frac{q}{e} = \frac{{161}}{{1,{{6.10}^{ - 19}}}}{\rm{ = 1,01}}{\rm{.1}}{{\rm{0}}^{21}}{\rm{ e}}\) c) Năng lượng mà nguồn cung cấp cho đèn là : \(A = EIt = Eq = 9.161 = 1,{45.10^3}{\rm{ J}}\) d) Công suất của nguồn là : \(P = \frac{A}{t} = EI = 9.1,34 = 12,1{\rm{ W}}\) 4.40. Một thiết bị làm nóng trong phòng thí nghiệm có điện trở 5,0 Ω. Thiết bị được nối với bộ acquy 12 V. Bỏ qua điện trở của acquy. Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Cường độ dòng điện qua điện trở: \(I = \frac{U}{R}\) Lời giải chi tiết: Bỏ qua điện trở của acquy => r = 0; U = E a) Cường độ dòng điện qua thiết bị là: \(I = \frac{E}{R} = \frac{{12}}{5} = 2,4{\rm{ A}}\) 4.41. Một bóng đèn pin đang sáng với hiệu điện thế giữa hai đầu bóng đèn là 2,2 V và cường độ dòng điện qua đèn là 0,25 A. Hãy tính: Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Cường độ dòng điện: \(I = \frac{{\Delta q}}{{\Delta t}}\) - Năng lượng điện tiêu thụ của đoạn mạch: A = UIt Lời giải chi tiết: a) Lượng điện tích đi qua bóng đèn trong một giây là 0,25 C. Năng lượng tiêu thụ trên bóng đèn khi mỗi culông điện tích truyền qua là: \(A = IUt = 0,25.2,2.4 = 2,2{\rm{ J}}\) 4.42. Một bóng đèn pin đang sáng với hiệu điện thế giữa hai đầu bóng đèn là 3,0 V và điện trở của bóng đèn là 15 Ω. Tính: Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Cường độ dòng điện qua một vật dẫn kim loại: \(I = \frac{U}{R}\) - Công suất mà nguồn cấp cho điện trở: P = EI = I2R - Năng lượng mà nguồn cấp cho điện trở: A = Pt Lời giải chi tiết: a) Cường độ dòng điện trong bóng đèn là: \(I = \frac{U}{R} = \frac{3}{{15}} = 0,2{\rm{ A}}\) 4.43. Người ta dùng số ampe-giờ (Ah) để biểu diễn năng lượng lưu trữ của pin hoặc acquy. Một acquy 60 Ah có thể cung cấp dòng điện có cường độ 60 A trong 1 giờ hoặc 30 A trong 2 giờ,... Tính năng lượng được lưu trữ trong acquy ô tô 12 V, 80 Ah (0,80.102 Ah), theo đơn vị J. Phương pháp giải: Vận dụng kiến thức đã học về năng lượng mà nguồn: A = UIt Lời giải chi tiết: Acquy ô tô 12 V có thể cung cấp dòng điện có cường độ 80 A trong 1 giờ. Năng lượng được lưu trữ trong acquy ô tô là: \(A = UIt = 12.80.3600 = 3,{5.10^6}{\rm{ J}}\) 4.44. Xét mạch điện ở Hình 4.12 và giả sử nguồn điện không có điện trở trong.
a) Ngay sau khi đóng công tắc, cường độ dòng điện chạy qua nguồn điện là A. 0. B. \(E/2R.\) C. \(2E/R.\) D. \(E/R.\) b) Sau một thời gian rất dài, cường độ dòng điện chạy qua nguồn là A. 0. B. \(E/2R.\) C. \(2E/R.\) D. \(E/R.\) Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Tụ điện: nạp, xả điện vào tụ khi mạch xoay chiều hoặc có sự biến đổi điện thế trong mạch. - Điện trở song song: \(\frac{1}{R} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + ... + \frac{1}{{{R_n}}}\); I = I1 + I2 + … + In ; U = U1 = U2 = … = Un - Điện trở nối tiếp: R = R1 + R2 + … + Rn; U = U1 + U2 + … + Un; I = I1 = I2 = … = In Lời giải chi tiết: a) Ngay sau khi đóng công tắc, dòng điện và điện áp trong mạch điện không ổn định nên vẫn nạp, xả điện vào tụ được, khi đó mạch có hai điện trở mắc song song. Điện trở tương đương là: \({R_b} = \frac{{R.R}}{{R + R}} = \frac{R}{2}\) cường độ dòng điện chạy qua nguồn điện là: \(I = \frac{E}{{{R_b}}} = \frac{{2E}}{R}\) b) Sau một thời gian rất dài đóng công tắc, dòng điện và điện áp trong mạch đã ổn định nên không thể nạp, xả điện vào tụ được, khi đó mạch có một điện trở. Điện trở tương đương là: \({R_b} = R\) cường độ dòng điện chạy qua nguồn điện là: \(I = \frac{E}{{{R_b}}} = \frac{E}{R}\) 4.45. Một bộ pin có suất điện động 12,0 V và điện trở trong r = 0,05 Ω. Người ta Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Khi mạch kín, hiệu điện thế: U = E – Ir = IR - Công suất cung cấp cho điện trở R: PR = I2R - Công suất cung cấp cho điện trở R: Pr = I2r - Công suất mà nguồn cung cấp: P = PR + Pr Lời giải chi tiết: a) Cường độ dòng điện trong mạch là: \(I = \frac{E}{{R + r}} = \frac{{12}}{{3 + 0,05}} = 3,93{\rm{ A}}\) Hiệu điện thế giữa hai cực của bộ pin là: \(U = E - Ir = 12,0 - 3,93.0,05 = 11,8{\rm{ V}}\) b) Công suất cung cấp cho điện trở R là: \({P_R} = {I^2}.R = 3,{93^2}.3 = 46,3{\rm{ W}}\) Công suất cung cấp cho điện trở trong r là: \({P_r} = {I^2}.r = 3,{93^2}.0,05 = 0,772{\rm{ W}}\) Công suất do bộ pin cung cấp là: \(P = {P_R} + {P_r} = 46,3 + 0,772 = 47,072{\rm{ W}}\) c) Cường độ dòng điện trong mạch là: \(I = \frac{E}{{R + r}} = \frac{{12}}{{3 + 2}} = 2,4{\rm{ A}}\) Hiệu điện thế giữa hai cực của bộ pin là: \(U = E - Ir = 12,0 - 2,4.2 = 7,2{\rm{ V}}\) Công suất cung cấp cho điện trở R là: \({P_R} = {I^2}.R = 2,{4^2}.3 = 17,3{\rm{ W}}\) Công suất cung cấp cho điện trở trong r là: \({P_r} = {I^2}.r = 2,{4^2}.2 = 11,5{\rm{ W}}\) Công suất do bộ pin cung cấp là: \(P = {P_R} + {P_r} = 17,3 + 11,5 = 28,8{\rm{ W}}\) 4.46. Một acquy có suất điện động 15,0 V. Hiệu điện thế giữa hai cực của acquy là 11,6 V khi nó cung cấp công suất điện 20,0 W cho điện trở ngoài R. Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Khi mạch kín, hiệu điện thế: U = E – Ir = IR - Công suất cung cấp cho điện trở R: \({P_R} = {I^2}R = \frac{{{U^2}}}{R} = UI\) - Điện trở trong của nguồn: \(r = \frac{{E - U}}{I}\) Lời giải chi tiết: a) Điện trở ngoài R là: \(R = \frac{{{U^2}}}{P} = \frac{{11,{6^2}}}{{20}} = 6,73{\rm{ }}\Omega \) b) Cường độ điện trường của mạch là: \(I = \frac{P}{U} = \frac{{20}}{{11,6}} = 1,72{\rm{ A}}\) Điện trở trong của acquy là: \(r = \frac{{E - U}}{I} = \frac{{15 - 11,6}}{{1,72}} = 1,97{\rm{ }}\Omega \) 4.47. Đèn pin ở Hình 2.2, trang 92 sách Vật lí 11 dùng hai pin mắc nối tiếp nhau. Mỗi pin có suất điện động 1,50 V. Một pin có điện trở trong 0,255 Ω, pin còn lại có điện trở trong 0,153 Ω. Khi đóng công tắc, cường độ dòng điện trong bóng đèn là 0,600 A. Tìm: Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Nguồn điện mắc nối tiếp: r = r1 + r2 + … + rn; E = E1 + E2 + … + En - Khi mạch kín, hiệu điện thế: U = E – Ir - Công suất tiêu thụ ở điện trở trong: \(P = {I^2}r\) Lời giải chi tiết: a) Mạch có 2 pin mắc nối tiếp và nối tiếp với đèn. \(E = I\left( {R + {r_b}} \right)\) Điện trở trong của nguồn là: \({r_b} = {r_1} + {r_2} = 0,255 + 0,153 = 0,408{\rm{ }}\Omega \) Điện trở của bóng đèn là: \(R = \frac{E}{I} - {r_b} = \frac{{1,5 + 1,5}}{{0,6}} - 0,408 = 4,6{\rm{ }}\Omega \) b) Công suất chuyển năng lượng ở điện trở trong là: \(P = {I^2}{r_b} = 0,{6^2}.0,408 = 0,145{\rm{ W}}\) 4.48. Một acquy ô tô có suất điện động 12,6 V và điện trở trong 0,080 Ω. Các đèn của ô tô (được mắc song song với nhau) có điện trở tương đương là 5,00 Ω (coi là không đổi). Phương pháp giải: Vận dụng kiến thức đã học về mạch điện: - Khi mạch kín, hiệu điện thế: U = E – Ir = IR - Khi mạch hở, hiệu điện thế: U = E = Ir Lời giải chi tiết: a) Khi acquy chỉ dùng để cấp điện cho các đèn. Cường độ dòng điện là: \(I = \frac{E}{{R + r}} = \frac{{12,6}}{{5 + 0,08}} = 2,48{\rm{ A}}\) Hiệu điện thế giữa hai đầu các bóng đèn là: \(U = IR = 2,48.5 = 12,4{\rm{ V}}\) b) Khi khởi động ô tô, cần thêm 35,0 A từ acquy. Gọi I1 và I2 lần lượt là cường độ dòng điện qua acquy và qua đèn. I1= I2 + 35 A I1r = E – I2r => E = I1r + I2r E = (I2 + 35).0,08 + I2.5 = 12,6 V => I2 = 1,93 A U2= 1,93.5 = 9,65 V |




















Danh sách bình luận