Phần câu hỏi bài 8 trang 132 Vở bài tập toán 8 tập 2Giải phần câu hỏi bài 8 trang 132 VBT toán 8 tập 2. Cho hình chóp tam giác đều S.ABC(h.90) có cạnh đáy AB = a, trung đoạn SD = b... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
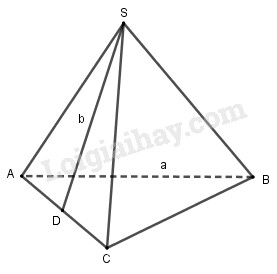
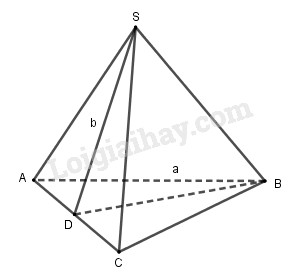
Cho hình chóp tam giác đều \(S.ABC\)(h.90) có cạnh đáy \(AB = a\), trung đoạn \(SD = b\).
Khoanh tròn vào chữ cái trước khẳng định đúng. LG a Khi \(a = 5cm\) và \(b = 6,5cm\) thì: \({a_1})\) Diện tích xung quanh của hình chóp là: A. \(48,75c{m^2}\) B. \(97,5c{m^2}\) C. \(84c{m^2}\) D. \(42c{m^2}\) \({a_2})\) Diện tích toàn phần của hình chóp (lấy đến hai chữ số thập phân) là: A. \(59,57c{m^2}\) B. \(59,58c{m^2}\) C. \(70,40c{m^2}\) D. \(52,83c{m^2}\) Khoanh tròn vào chữ cái trước khẳng định đúng. \({a_3})\) Độ dài cạnh bên của hình chóp (lấy đến hai chữ số thập phân) là: A. \(6,13cm\) B. \(6,31cm\) C. \(6,96cm\) D. \(6,69cm\) Phương pháp giải: Sử dụng công thức tính diện tích xung quanh hình chóp đều: \({S_{xq}} = p.d\) với \(p\) là nửa chu vi đáy, \(d\) là độ dài trung đoạn. Công thức tính diện tích toàn phần của hình chóp bằng tổng diện tích xung quanh và diện tích đáy. Sử dụng định lí Py-ta-go tính độ dài cạnh bên của hình chóp. Lời giải chi tiết: Với \(a = 5cm,b = 6,5cm\) thì: \({a_1})\) Nửa chu vi đáy là: \(\dfrac{{5 + 5 + 5}}{2} = 7,5\left( {cm} \right)\). Diện tích xung quanh hình chóp là: \(7,5.6,5 = 48,75\left( {c{m^2}} \right)\) Chọn A. \({a_2})\) Vì \(D\) là trung điểm \(AC\) nên \(BD \bot AC\).
Tam giác \(BDC\) có: \(B{D^2} = B{C^2} - C{D^2}\) \( = {5^2} - {\left( {\dfrac{5}{2}} \right)^2} = 18,75\) \( \Rightarrow BD \approx 4,33\left( {cm} \right)\) Diện tích tam giác \(ABC\) là: \(\dfrac{1}{2}BD.AC = \dfrac{1}{2}.4,33.5 = 10,83\) \(\left( {c{m^2}} \right)\) Diện tích toàn phần của hình chóp là: \(48,75 + 10,83 = 59,58\left( {c{m^2}} \right)\) Chọn B. \({a_3})\) Tam giác \(SDC\) vuông tại \(D\) nên áp dụng định lí Py-ta-go ta có: \(S{C^2} = S{D^2} + D{C^2}\) \( = 6,{5^2} + 2,{5^2} = 48,5\) \( \Rightarrow SC \approx 6,96\left( {cm} \right)\) Chọn C. LG b Khi diện tích xung quanh của hình chóp bằng \(58,32c{m^2}\) và trung đoạn \(b = 7,2cm\) thì độ dài \(a\) của cạnh đáy hình chóp đó là: A. \(14,4cm\) B. \(5,39cm\) C. \(7,9cm\) D. \(5,4cm\) Phương pháp giải: Sử dụng công thức tính diện tích xung quanh hình chóp đều \({S_{xq}} = p.d\) với \(p\) là nửa chu vi, \(d\) là độ dài trung đoạn. Lời giải chi tiết: Nửa chu vi đáy của hình chóp là: \(p = \dfrac{{{S_{xq}}}}{d} = \dfrac{{58,32}}{{7,2}} = 8,1\) Độ dài cạnh đáy là: \(a = \dfrac{{2p}}{3} = \dfrac{{2.8,1}}{3} = 5,4\left( {cm} \right)\) Chọn D. Loigiaihay.com
|




















Danh sách bình luận