Phần câu hỏi bài 6 trang 21 Vở bài tập toán 8 tập 1

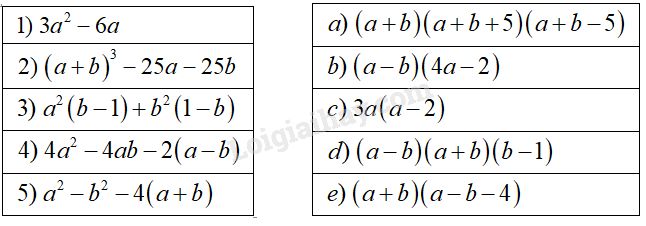
Câu 18.

Khoanh tròn vào chữ cái trước đẳng thức đúng.

\( (A)\,\,x\left( {x - y} \right) + y\left( { - x + y} \right) \)\(= \left( {x - y} \right)\left( {x + y} \right) \)

\( (B)\,\,x\left( {x + y} \right) - 6x - 6y \)\(= \left( {x + y} \right)\left( {x + 6} \right) \)

\((C)\,\,a\left( {b - c} \right) + {b^2} - {c^2} \)\(= \left( {b - c} \right)\left( {a + b - c} \right) \)

\( (D)\,\,{\left( {x - y} \right)^2} - {x^3} + {y^3} \)\(= \left( {x - y} \right)\left( {x - y - {x^2} - xy - {y^2}} \right) \) 

Phương pháp giải:

- Phân tích đa thức thành nhân tử là biến đổi đa thức đó thành một tích của các đa thức.

- Áp dụng hằng đẳng thức:

\(\eqalign{
& {A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right) \cr 
& {A^3} - {B^3} = \left( {A - B} \right)({A^2} + AB + {B^2}) \cr} \)

Giải chi tiết:

\(\eqalign{
& x\left( {x - y} \right) + y\left( { - x + y} \right) \cr 
& = x\left( {x - y} \right) + y\left[ { - \left( {x - y} \right)} \right] \cr 
& = x\left( {x - y} \right) - y\left( {x - y} \right) \cr 
& = \left( {x - y} \right)\left( {x - y} \right) = {\left( {x - y} \right)^2} \cr 
& x\left( {x + y} \right) - 6x - 6y \cr 
& = x\left( {x + y} \right) - 6\left( {x + y} \right) \cr 
& = \left( {x + y} \right)\left( {x - 6} \right) \cr 
& \,a\left( {b - c} \right) + {b^2} - {c^2} \cr 
& = a\left( {b - c} \right) + \left( {b - c} \right)\left( {b + c} \right) \cr 
& = \left( {b - c} \right)\left( {a + b + c} \right) \cr 
& \,{\left( {x - y} \right)^2} - {x^3} + {y^3} \cr 
& = {\left( {x - y} \right)^2} - \left( {{x^3} - {y^3}} \right) \cr 
& = {\left( {x - y} \right)^2} - \left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right) \cr 
& = \left( {x - y} \right)\left[ {x - y - \left( {{x^2} + xy + {y^2}} \right)} \right] \cr 
& = \left( {x - y} \right)\left( {x - y - {x^2} - xy - {y^2}} \right) \cr 
& = \left( {x - y} \right)\left( {x - y - {x^2} - xy - {y^2}} \right) \cr} \)

Chọn D.

Câu 19.

Nối một đa thức ở cột bên trái với một đa thức ở cột bên phải để được đẳng thức đúng.

Phương pháp giải:

- Phân tích đa thức ở cột bên trái thành nhân tử và so sánh kết quả đó với các đa thức ở cột bên phải.

Giải chi tiết:

\(1)\,\,3{a^2} - 6a = 3a\left( {a - 2} \right)\)

\(\eqalign{
& 2)\,\,{\left( {a + b} \right)^3} - 25a - 25b \cr 
& = {\left( {a + b} \right)^3} - 25\left( {a + b} \right) \cr 
& = \left( {a + b} \right)\left[ {{{\left( {a + b} \right)}^2} - 25} \right] \cr 
& = \left( {a + b} \right)\left[ {{{\left( {a + b} \right)}^2} - {5^2}} \right] \cr 
& = \left( {a + b} \right)\left( {a + b + 5} \right)\left( {a + b - 5} \right) \cr} \)

\(\eqalign{
& 3)\,\,{a^2}\left( {b - 1} \right) + {b^2}\left( {1 - b} \right) \cr 
& = {a^2}\left( {b - 1} \right) - {b^2}\left( {b - 1} \right) \cr 
& = \left( {b - 1} \right)\left( {{a^2} - {b^2}} \right) \cr 
& = \left( {b - 1} \right)\left( {a - b} \right)\left( {a + b} \right) \cr 
& = \left( {a - b} \right)\left( {a + b} \right)\left( {b - 1} \right) \cr} \) 

\(\eqalign{
& 4)\,\,4{a^2} - 4ab - 2\left( {a - b} \right) \cr 
& = 4a\left( {a - b} \right) - 2\left( {a - b} \right) \cr 
& = \left( {a - b} \right)\left( {4a - 2} \right) \cr} \)

\(\eqalign{
& 5)\,\,{a^2} - {b^2} - 4\left( {a + b} \right) \cr 
& = \left( {a - b} \right)\left( {a + b} \right) - 4\left( {a + b} \right) \cr 
& = \left( {a + b} \right)\left( {a - b - 4} \right) \cr} \)

Do đó ta nối như sau:

1 – c; 2 – a; 3 – d; 4 – b; 5 – e.

Câu 20.

Điều dấu “x” vào ô trống thích hợp.

Phương pháp giải:

- Đưa các đẳng thức về dạng \(A(x) = 0\)

- Phân tích đa thức ở vế trái thành nhân tử.

- Áp dụng tính chất đa thức bằng \(0\) nếu nó chứa nhân tử bằng \(0.\)

\(B\left( x \right)C\left( x \right) = 0 \Rightarrow \left[ \begin{array}{l}B\left( x \right) = 0\\C\left( x \right) = 0\end{array} \right.\)

Giải chi tiết:

\(\begin{array}{l}{x^2} - 16 = 4\left( {x + 4} \right)\\{x^2} - {4^2} - 4\left( {x + 4} \right) = 0\\\left( {x - 4} \right)\left( {x + 4} \right) - 4\left( {x + 4} \right) = 0\\\left( {x + 4} \right)\left( {x - 4 - 4} \right) = 0\\\left( {x + 4} \right)\left( {x - 8} \right) = 0\\ \Rightarrow \left[ \begin{array}{l}x + 4 = 0\\x - 8 = 0\end{array} \right. \Rightarrow \left[ \begin{array}{l}x =  - 4\\x = 8\end{array} \right.\end{array}\)

\(\begin{array}{l}{x^3} - 9{x^2} = 45 - 5x\\{x^3} - 9{x^2} + 5x - 45 = 0\\{x^2}\left( {x - 9} \right) + 5\left( {x - 9} \right) = 0\\\left( {x - 9} \right)\left( {{x^2} + 5} \right) = 0\\ \Rightarrow x - 9 = 0\\ \Rightarrow x = 9\end{array}\)

Vì \({x^2} \ge 0\,\,\) với mọi x nên \({x^2} + 5 > 0\)  với mọi \(x.\) 

\(\begin{array}{l}{x^2} - 27 + {x^2}\left( { - {x^2} + 27} \right) = 0\\{x^2} - 27 - {x^2}\left( {{x^2} - 27} \right) = 0\\\left( {{x^2} - 27} \right)\left( {1 - {x^2}} \right) = 0\\\left( {x - \sqrt {27} } \right)\left( {x + \sqrt {27} } \right)\left( {1 - x} \right)\left( {1 + x} \right) = 0\\ \Rightarrow \left[ \begin{array}{l}x - \sqrt {27}  = 0\\x + \sqrt {27}  = 0\\1 - x = 0\\1 + x = 0\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = \sqrt {27} \\x =  - \sqrt {27} \\x = 1\\x =  - 1\end{array} \right.\end{array}\)  

Ta có bảng sau:

Loigiaihay.com