Phần câu hỏi bài 4 trang 97, 98 Vở bài tập toán 9 tập 2

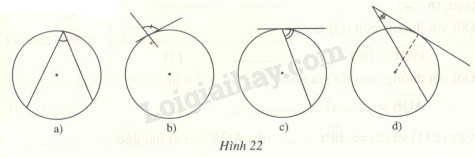
Câu 9

Khoanh tròn vào chữ cái dưới hình chỉ góc tạo bởi tia tiếp tuyến và dây cung trong hình 22.

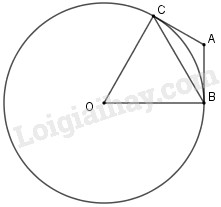
Phương pháp giải:

Sử dụng định nghĩa góc tạo bởi tiếp tuyến và dây cung : “Góc tạo bởi tiếp tuyến và dây cung là góc có đỉnh tại tiếp điểm, một cạnh là tia tiếp tuyến và cạnh kia chứa dây cung”.

Lời giải chi tiết:

Theo định nghĩa ta thấy chỉ có hình c thỏa mãn.

Chọn C. 

Câu 10

Cho đường tròn (O ; R) và dây cung BC bằng R. Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau ở A. Số đo của góc BAC là: 

(A) 95^o                                     (B) 100^o

(C) 110^o                                   (D) 120^o

Khoanh tròn vào chữ cái trước kết quả đúng. 

Phương pháp giải:

Chứng minh tam giác \(OBC\) đều

Sử dụng tổng bốn góc trong tứ giác bằng \(360^\circ \) để tính \(\widehat {BAC}\).

Lời giải chi tiết:

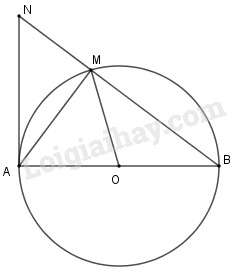
Xét tam giác \(OBC\) có \(OB = OB = R = BC \Rightarrow \Delta OBC\) đều nên \(\widehat {BOC} = 60^\circ \)

Xét \(\left( O \right)\) có \(AC,AB\) là hai tiếp tuyến nên \(\widehat {OCA} = \widehat {OBA} = 90^\circ \)

Xét tứ giác \(OBAC\) có \(\widehat O + \widehat {OCA} + \widehat {OBA} + \widehat {BAC} = 360^\circ  \)\(\Leftrightarrow 60^\circ  + 90^\circ  + 90^\circ  + \widehat {BAC} = 360^\circ \)\( \Rightarrow \widehat {BAC} = 120^\circ .\)

Chọn D.

Câu 11.

Cho đường tròn tâm O, đường kính AB, lấy điểm M khác A và B trên đường tròn. Gọi N là giao điểm của BM với tiếp tuyến A của đường tròn. Biết \(\widehat {BOM} = {120^o}\) . Số đo của góc NAM là:

(A) 20^o                                     (B) 30^o

(C) 45^o                                     (D) 60^o

Khoanh tròn vào chữ cái trước kết quả đúng. 

Phương pháp giải:

Sử dụng tính chất tia tiếp tuyến, tính chất tam giác đều và tính chất hai góc kề bù.

Lời giải chi tiết:

Ta có \(\widehat {MOB} + \widehat {MOA} = 180^\circ \) (hai góc kề bù)  nên \(\widehat {MOA} = 180^\circ  - 120^\circ  = 60^\circ \) 

Xét tam giác \(OMA\) có \(OA = OM\) (= bán kính) lại có \(\widehat {MOA} = 60^\circ  \Rightarrow \Delta OMA\) là tam giác đều nên \(\widehat {MAO} = 60^\circ \)

Lại có \(AN\) là tiếp tuyến của \(\left( O \right) \Rightarrow AB \bot NA \Rightarrow \widehat {NAB} = 90^\circ \)

Từ đó \(\widehat {MAN} = \widehat {NAB} - \widehat {MAO}\)\( = 90^\circ  - 60^\circ  = 30^\circ .\)

Chọn B.

Loigiaihay.com