Giải mục 5 trang 17, 18, 19, 20 Chuyên đề học tập Toán 11 - Cánh diềuTrong mặt phẳng, cho điểm O cố định. Với mỗi điểm M (M khác O) trong mặt phẳng, hãy xác định điểm M' sao cho OM' = OM và góc lượng giác (OM, OM') = 90° (Hình 26). Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
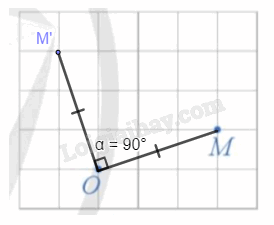
Hoạt động 13 Trong mặt phẳng, cho điểm O cố định. Với mỗi điểm M (M khác O) trong mặt phẳng, hãy xác định điểm M' sao cho OM' = OM và góc lượng giác (OM, OM') = 90° (Hình 26).
Phương pháp giải: - Nếu tia Om quay quanh gốc O của nó theo một chiều cố định bắt đầu từ vị trí tia Oa và dừng ở vị trí tia Ob thì ta nói tia Om quét một góc lượng giác có tia đầu Oa, tia cuối Ob. Kí hiệu: (Oa, Ob). - Xác định điểm M' thỏa mãn điều kiện: OM' = OM và góc lượng giác (OM, OM') = 90° Lời giải chi tiết:
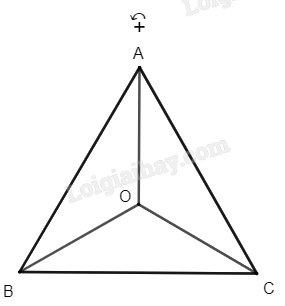
Cách xác định: - Nối O với M; - Qua O kẻ đường thẳng vuông góc với OM, trên đường thẳng, lấy điểm M' theo chiều dương sao cho OM' = OM. Luyện tập 8 Cho tam giác đều ABC có trọng tâm O. Xác định ảnh của các điểm A, B, C, qua phép quay tâm O với góc quay – 120°. Phương pháp giải: Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay. Lời giải chi tiết:
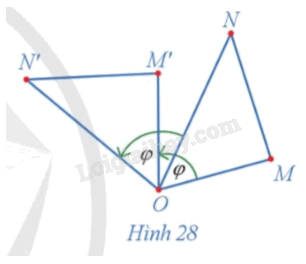
Ta có tam giác ABC đều có O là trọng tâm nên \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = 120^\circ \) và \(OA{\rm{ }} = {\rm{ }}OB{\rm{ }} = {\rm{ }}OC\). Vì phép quay với góc quay – 120° có chiều quay cùng chiều kim đồng hồ nên ảnh của các điểm A, B, C qua phép quay tâm O với góc quay – 120° lần lượt là các điểm C, A, B. Hoạt động 14 Trong Hình 28, cho các điểm M', N' lần lượt là ảnh của các điểm M, N qua phép quay tâm O với góc quay φ. a) Hai tam giác OM'N' và OMN có bằng nhau hay không? b) So sánh hai đoạn thẳng M'N' và MN.
Phương pháp giải: Xét 2 tam giác OM'N' và OMN bằng nhau theo trường hợp c – g – c. Từ đó so sánh hai đoạn thẳng M'N' và MN. Lời giải chi tiết:
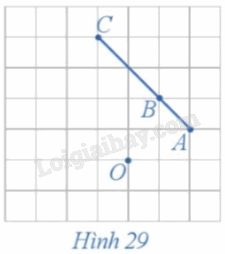
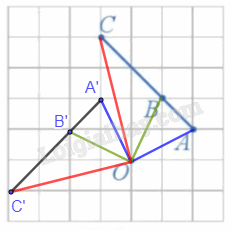
a) Vì M', N' lần lượt là ảnh của các điểm M, N qua phép quay tâm O với góc quay \(\varphi \) nên \(OM{\rm{ }} = {\rm{ }}OM',{\rm{ }}ON{\rm{ }} = {\rm{ }}ON'.\) Ta có: \(\begin{array}{l}\widehat {MON} + \widehat {NOM'} = \widehat {MOM'} = \varphi \\\widehat {NOM'} + \widehat {M'ON'} = \widehat {NON'} = \varphi \end{array}\) Suy ra \(\widehat {MON} = \widehat {M'ON'}\) Xét hai tam giác OM'N' và OMN ta có: OM = OM' (cmt) \(\widehat {MON} = \widehat {M'ON'}\) cmt) ON = ON' (cmt) Do đó, hai tam giác OM'N' và OMN bằng nhau (c – g – c). b) Từ \(\Delta OM'N'{\rm{ }} = {\rm{ }}\Delta OMN\), suy ra M'N' = MN (hai cạnh tương ứng). Hoạt động 15 Xét phép quay tâm O với góc quay 90° (Hình 29). a) Xác định các điểm A', B', C' lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép quay trên. b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Phương pháp giải: Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay. Lời giải chi tiết:
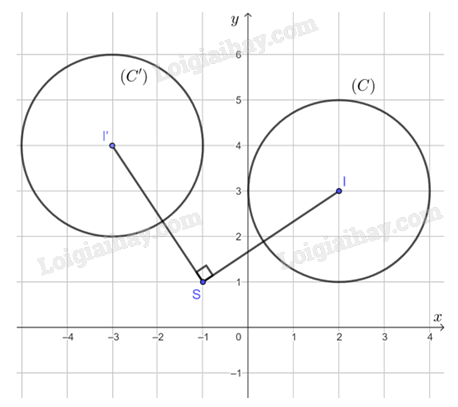
a) Các điểm A', B', C' lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép quay tâm O, góc quay 90° được xác định như hình vẽ trên. b) Nhận thấy ba điểm A', B', C' thẳng hàng và B' nằm giữa A' và C'. Luyện tập 9 Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(2; 3) bán kính R = 2. Xác định ảnh của (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90°. Phương pháp giải: Tìm ảnh của tâm I qua phép quay bằng cách: Phép quay tâm O, góc 900: Khi đó: \(\left\{ \begin{array}{l}x' = - y\\y' = x\end{array} \right.\) Từ đó xác định ảnh của (C) Lời giải chi tiết: Ảnh của đường tròn (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90° là một đường tròn có bán kính R' = R = 2, gọi là (C'). Gọi I' là tâm của đường tròn (C'). Khi đó ta có I' là ảnh của I qua phép quay tâm S(– 1; 1) với góc quay φ = 90°. Suy ra I'(– 3; 4).
Vậy ảnh đường tròn (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90° là đường tròn (C') có tâm I'(– 3; 4), bán kính R' = 2.
|






















Danh sách bình luận