Giải mục 3 trang 40, 41 SGK Toán 8 - Cùng khám pháTrong Hình 6.11, tam giác \(ABC\) được vẽ trên giấy vở học sinh. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
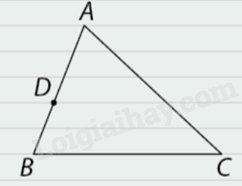
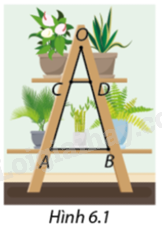
Hoạt động 3 Trong Hình 6.11, tam giác \(ABC\) được vẽ trên giấy vở học sinh. 1. Tính tỉ số \(\frac{{AD}}{{BD}}.\) 2. Xác định điểm \(E\) trên cạnh \(AC\) sao cho \(\frac{{DA}}{{DB}} = \frac{{EA}}{{EC}}.\) Có bao nhiêu điểm như vậy? 3. Theo em, \(DE\) có song somg với \(BC\) không? Phương pháp giải: Quan sát hình 6.11 tính tỉ số \(\frac{{AD}}{{BD}}\) sau đó xác định điểm E sao cho \(\frac{{DA}}{{DB}} = \frac{{EA}}{{EC}}\). Lời giải chi tiết: 1. Tỉ số \(\frac{{AD}}{{BD}} = \frac{3}{2}\). 2. Để \(\frac{{DA}}{{DB}} = \frac{{EA}}{{EC}}\) thì điểm E phải nằm trên đoạn thẳng AC và có tỉ lệ: \(\frac{{EA}}{{EC}} = \frac{3}{2}\). => chỉ có một điểm như vậy 3. Theo em, \(DE\) song song với \(BC\). Luyện tập 4 Trong Hình 6.14, đường thẳng \(DE\) và \(FG\) có song song với \(AC\) không? Vì sao? Phương pháp giải: Dựa vào định lí Thales đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác. Lời giải chi tiết: Xét hai đường thẳng \(DE;AC\), ta có: \(\begin{array}{l}\frac{{DB}}{{DA}} = \frac{{3,5 + 4,5}}{6} = \frac{4}{3}\\\frac{{EB}}{{EC}} = \frac{{4 + 6}}{{7,5}} = \frac{4}{3}\\ = > \frac{{DB}}{{DA}} = \frac{{EB}}{{EC}} = \frac{4}{3}\end{array}\) Dựa vào định lí Thales đảo suy ra \(DE//AC\) Xét hai đường thẳng \(FG;AC\), ta có: \(\begin{array}{l}\frac{{FB}}{{FA}} = \frac{{3,5}}{{4,5 + 6}} = \frac{1}{3}\\\frac{{GB}}{{GC}} = \frac{4}{{6 + 7,5}} = \frac{8}{{27}}\\ = > \frac{{FB}}{{FA}} \ne \frac{{GB}}{{GC}}\end{array}\) Dựa vào định lí Thales đảo suy ra \(FG\) không song song với \(AC\) Vận dụng 2 Quay lại bài toán khởi động (hình 6.1): Chỉ dùng thước đo độ dài, làm cách nào để có thể xác định được các cạnh \(AB\) và \(CD\) của hai mặt kệ có song song với nhau không? Em hãy giải thích bằng cách nào bác thợ mộc có thể xác định được cạnh của hai tầng kệ chữ \(A\) song song với nhau mà chỉ dùng thước đo độ dài. Phương pháp giải: Dựa vào định lí Thales đảo để xác định xem các cạnh \(AB\) và \(CD\) của hai mặt kệ có song song với nhau không. Lời giải chi tiết: Quan sát hình 6.1 ta có: \(\begin{array}{l}\frac{{CO}}{{CA}} = \frac{1}{3}\\\frac{{DO}}{{DB}} = \frac{1}{3}\end{array}\) Dựa vào định lí Thales đảo nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác, ta thấy: \(\frac{{CO}}{{CA}} = \frac{{DO}}{{DB}} = \frac{1}{3}\) (mà các đoạn thẳng này tương ứng tỉ lệ với nhau) => \(CD//AB\)
|






















Danh sách bình luận