Giải mục 3 trang 40, 41, 42, 43 Chuyên đề học tập Toán 11 - Cánh diều

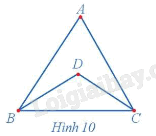
Hoạt động 7

Quan sát đồ thị ở Hình 10 và đường đi CABDCB, cho biết:

a) Đường đi trên có đi qua tất cả các cạnh của đồ thị hay không?

b) Đường đi trên đi qua mỗi cạnh bao nhiêu lần? 

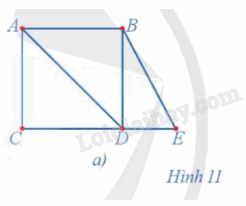
Phương pháp giải:

Quan sát hình 10 để trả lời

Lời giải chi tiết:

Quan sát đồ thị ở Hình 10 ta thấy:

a) Đường đi CABDCB đi qua tất cả các cạnh của đồ thị.

b) Đường đi trên đi qua mỗi cạnh đúng một lần.

Luyện tập 7

Hãy chỉ ra hai đường đi Euler trong đồ thị ở Hình 11a.

Phương pháp giải:

Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng 1 lần.

Lời giải chi tiết:

Hình 11a có đường đi Euler BEDBADCA và đường đi Euler BEDCADBA.

Luyện tập 8

Chứng minh rằng đồ thị ở Hình 11a không có chu trình Euler.

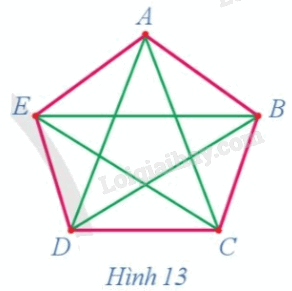
Phương pháp giải:

Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng 1 lần.

Nếu chu trình là đường đi Euler thì chu trình đo được gọi là chu trình Euler.

Lời giải chi tiết:

Ta có d(A) = 3, d(B) = 3 nên đồ thị ở Hình 11a có đỉnh bậc lẻ, do đó theo định lí Euler, đồ thị ở Hình 11a không có chu trình Euler.

Hoạt động 8

Quan sát đường đi màu đỏ trên đồ thị ở Hình 13 và cho biết đường đi đó có đi qua tất cả các đỉnh của đồ thị hay không và mỗi đỉnh đi qua bao nhiêu lần.

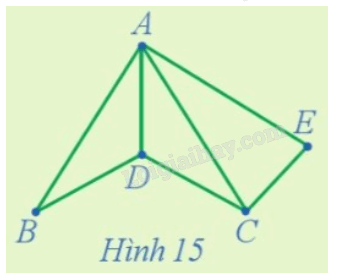
Phương pháp giải:

Quan sát hình 13 để trả lời

Lời giải chi tiết:

Quan sát đường đi màu đỏ trên đồ thị ở Hình 13 ta thấy đường đi đó đi qua tất cả các đỉnh của đồ thị hay và mỗi đỉnh đi qua đúng một lần.

Luyện tập 9

 Tìm hai đường đi Hamilton bắt đầu từ đỉnh E của đồ thị trong Hình 15.

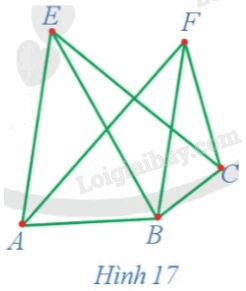
Phương pháp giải:

Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả các đinht của đồ thị, mỗi đỉnh đúng 1 lần.

Lời giải chi tiết:

Quan sát đồ thị Hình 15, ta thấy rằng hai đường đi Hamilton bắt đầu từ đỉnh E của đồ thị này là EACDB và ECDBA.

Luyện tập 10

Chứng minh rằng đồ thị G ở Hình 17 có ít nhất một chu trình Hamilton. 

Phương pháp giải:

Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả các đinht của đồ thị, mỗi đỉnh đúng 1 lần.

Nếu chu trình là đường đi Hamilton thì chu trình đó được gọi là chu trình Hamilton

Lời giải chi tiết:

Ta có: d(A) = 3, d(B) = 4, d(C) = 3, d(E) = 3, d(F) = 3. Đồ thị G ở Hình 17 gồm 5 đỉnh, mỗi đỉnh của đồ thị đều có bậc không nhỏ hơn \(\frac{5}{2}\) . Do đó, theo định lí Dirac, đồ thị G có ít nhất một chu trình Hamilton.

Luyện tập 11

Chứng minh rằng đồ thị G ở Hình 19 có ít nhất một chu trình Hamilton.

Phương pháp giải:

Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả các đinht của đồ thị, mỗi đỉnh đúng 1 lần.

Nếu chu trình là đường đi Hamilton thì chu trình đó được gọi là chu trình Hamilton.

Lời giải chi tiết:

Đồ thị G ở Hình 19 gồm 6 đỉnh, trong đó các đỉnh A, D, E có bậc 4, các đỉnh B, C có bậc 5 và đỉnh F có bậc 2 nên tổng bậc của hai đỉnh không kề nhau bất kì đều không nhỏ hơn 6. Do đó, theo định lí Ore, đồ thị G có ít nhất một chu trình Hamilton.