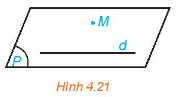
Giải mục 2 trang 80, 81, 82 SGK Toán 11 tập 1 - Kết nối tri thức

HĐ 2

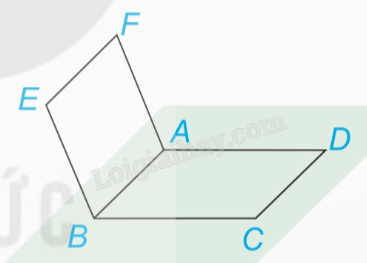
Trong không gian, cho một đường thẳng d và một điểm M không nằm trên d (H.4.21). Gọi (P) là mặt phẳng chứa M và d.

a) Trên mặt phẳng (P) có bao nhiêu đường thẳng đi qua M và song song với d?

b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) hay không?

Phương pháp giải:

Trong không gian, qua một điểm không nằm trên dường thẳng cho trước, có đúng một đường thẳng song song với đường thẳng đã cho

Lời giải chi tiết:

a) Có duy nhất một đường thẳng đi qua M song song với d

b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) vì hai đường thẳng song song đồng phẳng

HĐ 3

Quan sát lớp học và tìm hai đường thẳng song song với mép trên của bảng. Hai đường thẳng đó có song song với nhau hay không?

Phương pháp giải:

Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau

Lời giải chi tiết:

Đường thẳng song song với mép trên của bảng: Mép dưới của bảng, chân tường bục giảng

Hai đường thẳng đó cũng song song với nhau

LT 3

Trong Ví dụ 1, chứng minh rằng 4 điểm C, D, E, F đồng phẳng và tứ giác CDFE là hình bình hành.

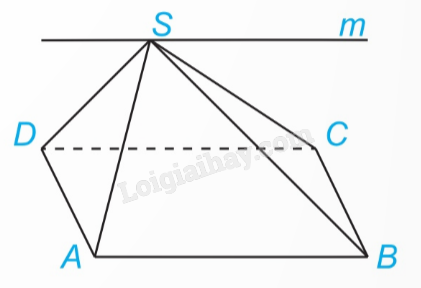
Phương pháp giải:

Để chứng minh bốn điểm: C, D, E, F đồng phẳng ta có thể chứng minh hai đường thẳng AB và CD song song

Dựa vào dấu hiệu tứ giác là hình bình hành để chứng minh CDEF là hình bình hành

Lời giải chi tiết:

Xét hình bình hành ABCD ta có: AB // CD, AB = CD

Xét hình bình hành ABEF ta có: AB // EF, AB = EF

Suy ra EF//CD, EF = CD

Suy ra CDEF là hình bình hành và C, D, E, F đồng phẳng

HĐ 4

Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến c. Một mặt phẳng (R) cắt (P) và (Q) lần lượt theo giao tuyến a và b khác c

a) Nếu hai đường thẳng a và c cắt nhau tại M thì đường thẳng b có đi qua M hay không (H.4.23)? Giải thích vì sao.

b) Nếu hai đường thẳng a và c song song với nhau thì hai đường thẳng b và c có song song với nhau hay không (H.4.24)? Giải thích vì sao. 

Phương pháp giải:

Nếu ba mặt phẳng đôi một cắt nhau, theo ba giao tuyến phân biệt thì ba giao tuyến đó đồng quy hoặc đôi một song song với nhau

Lời giải chi tiết:

a) M thuộc c suy ra M nằm trên mp(Q)

M thuộc a suy ra M nằm trên mp(R)

M cùng thuộc mp(R) và (Q) suy ra M nằm trên giao tuyến của mp(R) và (Q)

Như vậy , M thuộc b

LT 4

Trong Ví dụ 4, hãy xác định giao tuyến của hai mặt phẳng (SAD) và (SBC)

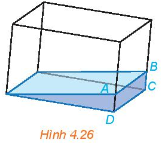
Phương pháp giải:

Để xác định giao điểm của một đường thẳng và một mặt phẳng, ta có thể tìm giao điểm của đường thẳng đó với một đường thẳng nằm trong mặt phẳng đã cho.

Lời giải chi tiết:

Hai mp(SAD) và (SBC) có điểm chung S và chứa hai đường thẳng song song AD và BC.

Do đó, giao tuyến của hai mp(SAD) và (SBC) là đường thẳng n đi qua S song cong với AD và BC

VD 2

Một bề kính chứa nước có đáy là hình chữ nhật được đặt nghiêng như Hình 4.26. Giải thích tại sao đường mép nước AB song song với cạnh CD của bề nước

Phương pháp giải:

Nếu hai mặt phẳng chứa hai đường thẳng song song với nhau thì giao tuyến của chúng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó

Lời giải chi tiết:

Ta có: \(mp\left( {ABKI} \right) \cap mp\left( {CDIK} \right) = IK\)

\(mp\left( {ABKI} \right) \cap mp\left( {ABCD} \right) = AB\)

\(mp\left( {CDIK} \right) \cap \left( {ABCD} \right) = CD\)

Mà IK // CD (Do CDIK là hình chữ nhật) suy ra AB // CD.