Giải mục 2 trang 37, 38 Chuyên đề học tập Toán 11 - Kết nối tri thức

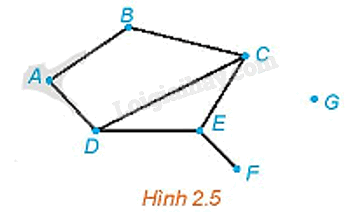
Hoạt động 4

Cho đồ thị như Hình 2.5. Tìm các đỉnh là đầu mút của: 0 cạnh; 1 cạnh; 2 cạnh; 3 cạnh.

Phương pháp giải:

Dựa vào hình 2.5 để làm

Lời giải chi tiết:

Đỉnh là đầu mút của 0 cạnh là đỉnh G.

Đỉnh là đầu mút của 1 cạnh là đỉnh F.

Các đỉnh là đầu mút của 2 cạnh là các đỉnh A, B.

Các đỉnh là đầu mút của 3 cạnh là các đỉnh C, D, E.

Luyện tập 4

Chứng minh rằng không có đơn đồ thị với 12 đỉnh và 28 cạnh mà các đỉnh đều có bậc 3 hoặc 4.

Phương pháp giải:

Trong một đồ thị, tổng tất cả bậc của đỉnh là một số chẵn và bằng hai lần số cạnh của đồ thị

Lời giải chi tiết:

Giả sử có đồ thị thỏa mãn yêu cầu bài toán. Gọi x là số đỉnh bậc 3 của đồ thị.

Khi đó, ta có số đỉnh bậc 4 là: \(12{\rm{ }}-{\rm{ }}x.\)

Tổng số bậc của các đỉnh là: \(3x{\rm{ }} + {\rm{ }}4\left( {12{\rm{ }}-{\rm{ }}x} \right).\)

Vì đồ thị có 28 cạnh nên theo Định lí bắt tay thì đồ thị có tổng số bậc là \(28{\rm{ }}.{\rm{ }}2{\rm{ }} = {\rm{ }}56.\)

Do đó, ta có phương trình \(3x{\rm{ }} + {\rm{ }}4\left( {12{\rm{ }}-{\rm{ }}x} \right){\rm{ }} = {\rm{ }}56\), tức là \(8{\rm{ }} + {\rm{ }}x{\rm{ }} = {\rm{ }}0\). Phương trình này không có nghiệm là số tự nhiên, do đó không tồn tại đồ thị thỏa mãn điều kiện đề bài.