Giải mục 1 trang 74, 75 SGK Toán 8 – Cánh diều

HĐ1

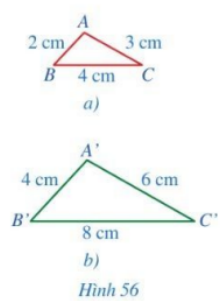
Quan sát Hình 56 và so sánh các tỉ số: \(\frac{{A'B'}}{{AB}};\,\,\frac{{A'C'}}{{AC}};\,\,\frac{{B'C'}}{{BC}}\).

Phương pháp giải:

Tính tỉ số giữa các cạnh rồi so sánh.

Lời giải chi tiết:

\(\begin{array}{l}\frac{{A'B'}}{{AB}} = \frac{2}{4} = \frac{1}{2}\\\frac{{A'C'}}{{AC}} = \frac{3}{6} = \frac{1}{2}\\\frac{{B'C'}}{{BC}} = \frac{4}{8} = \frac{1}{2}\end{array}\)

Ta thấy \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)

LT1

Cho tam giác ABC có trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm của AG, BG, CG. Chứng minh \(\Delta A'B'C' \backsim\Delta ABC\).

Phương pháp giải:

Tính tỉ số giữa các cạnh rồi chứng minh đồng dạng bằng trường hợp đồng dạng thứ nhất.

Lời giải chi tiết:

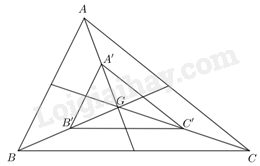
Vì A’, B’, C’ lần lượt là trung điểm của AG, BG, CG nên A’B’, B’C’, A’C’ lần lượt là đường trung bình của các tam giác AGB, BGC, AGC.

Khi đó: \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}} = \frac{1}{2}\)

Xét tam giác A’B’C’ và tam giác ABC có:

\(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}} = \frac{1}{2}\)

Vậy \(\Delta A'B'C' \backsim\Delta ABC\) (c-c-c)