Giải mục 1 trang 20, 21 Chuyên đề học tập Toán 11 - Chân trời sáng tạo

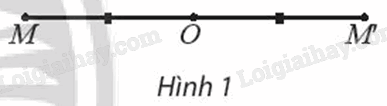
Khám phá 1

Cho điểm O. Gọi f là quy tắc xác định như sau:

a) Với điểm M khác O, xác định điểm M’ sao cho O là trung điểm của MM’ (Hình 1).

b) Với điểm M trùng với O thì f biến điểm M thành chính nó.

Hỏi f có phải là phép biến hình không?

Phương pháp giải:

Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M' = f(M)\).

Lời giải chi tiết:

Theo đề, ta có M’ = f(M).

Ta thấy f là một quy tắc sao cho ứng với mỗi điểm M đều xác định duy nhất một điểm M’.

Vậy f là một phép biến hình.

Thực hành 1

Trong mặt phẳng tọa độ Oxy, cho các điểm I(1; 1), M(2; 2), N(0; –3) và P(–1; –2). Tìm tọa độ các điểm \(M'{\rm{ }} = {\rm{ }}{Đ_I}\left( M \right),{\rm{ }}N'{\rm{ }} = {\rm{ }}{Đ_I}\left( N \right),{\rm{ }}P'{\rm{ }} = {\rm{ }}{Đ_I}\left( P \right).\)

Phương pháp giải:

Nếu  thì \(\left\{ \begin{array}{l}{x_{M'}} + {x_M} = 2{x_I}\\{y_{M'}} + {y_M} = 2{y_I}\end{array} \right.\) (I là trung điểm của MM’)

Lời giải chi tiết:

+ Ta có \(M'{\rm{ }} = {\rm{ }}{Đ_I}\left( M \right).\)

Suy ra I(1; 1) là trung điểm MM’ với M(2; 2).

Do đó \(\left\{ \begin{array}{l}{x_{M'}} = 2{x_I} - {x_M} = 2.1 - 2 = 0\\{y_{M'}} = 2{y_I} - {y_M} = 2.1 - 2 = 0\end{array} \right.\)

Suy ra M’ có tọa độ là (0; 0).

+ Ta có \(N'{\rm{ }} = {\rm{ }}{Đ_I}\left( N \right).\)

Suy ra I(1; 1) là trung điểm của NN’ với N(0; –3).

Do đó \(\left\{ \begin{array}{l}{x_{N'}} = 2{x_I} - {x_N} = 2.1 - 0 = 2\\{y_{N'}} = 2{y_I} - {y_N} = 2.1 + 3 = 5\end{array} \right.\)

Suy ra N’ có tọa độ là N’(2; 5).

+ Ta có \(P' = {\rm{ }}{Đ_I}\left( P \right).\)

Suy ra I(1; 1) là trung điểm PP’ với P(–1; –2).

Do đó \(\left\{ \begin{array}{l}{x_{P'}} = 2{x_I} - {x_P} = 2.1 + 1 = 3\\{y_{P'}} = 2{y_I} - {y_P} = 2.1 + 2 = 4\end{array} \right.\)

Suy ra P’ có tọa độ là P’(3; 4).

Vậy \(M'\left( {0;{\rm{ }}0} \right),{\rm{ }}N'\left( {2;{\rm{ }}5} \right),{\rm{ }}P'\left( {3;{\rm{ }}4} \right).\)

Vận dụng 1

Tìm phép đối xứng tâm biến mỗi hình sau thành chính nó.

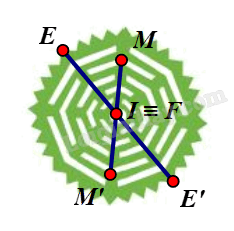
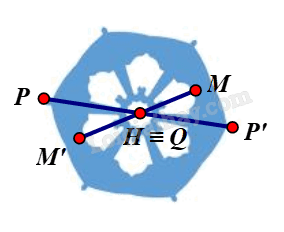
Phương pháp giải:

Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O  là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu . Điểm O được gọi là tâm đối xứng.

Lời giải chi tiết:

⦁ Ta xét hình màu đỏ:

Giả sử ta chọn điểm O trên hình màu đỏ như hình vẽ.

Lấy điểm B trùng O. Khi đó qua O, điểm đối xứng với B là chính nó.

Lấy điểm A bất kì trên hình màu đỏ sao cho A ≠ O.

Khi đó ta luôn xác định được một điểm A’ sao cho O là trung điểm của đoạn AA’.

Tương tự như vậy, với mỗi điểm M bất kì khác O trên hình màu đỏ, ta đều xác định được một điểm M’ trên hình sao cho O là trung điểm của đoạn MM’.

Vậy phép đối xứng tâm O biến hình màu đỏ thành chính nó.

⦁ Ta xét hình màu xanh lá:

Giả sử ta chọn điểm I trên hình màu xanh lá như hình vẽ.

Lấy điểm F trùng I. Khi đó qua I, điểm đối xứng với F là chính nó.

Lấy điểm E bất kì trên hình màu xanh lá sao cho E ≠ I.

Khi đó ta luôn xác định được một điểm E’ sao cho I là trung điểm của đoạn EE’.

Tương tự như vậy, với mỗi điểm M bất kì khác I trên hình màu xanh lá, ta đều xác định được một điểm M’ trên hình sao cho I là trung điểm của đoạn MM’.

Vậy phép đối xứng tâm I biến hình màu xanh lá thành chính nó.

⦁ Ta xét hình màu xanh biển:

Giả sử ta chọn điểm H trên hình màu xanh biển như hình vẽ.

Lấy điểm P trùng H. Khi đó qua H, điểm đối xứng với P là chính nó.

Lấy điểm P bất kì trên hình màu xanh biển sao cho P ≠ H.

Khi đó ta luôn xác định được một điểm P’ sao cho H là trung điểm của đoạn PP’.

Tương tự như vậy, với mỗi điểm M bất kì khác H trên hình màu xanh biển, ta đều xác định được một điểm M’ trên hình sao cho H là trung điểm của đoạn MM’.

Vậy phép đối xứng tâm H biến hình màu xanh biển thành chính nó.