Đề thi học kì 1 môn toán lớp 6 năm 2019 - 2020 trường THCS Tây Mỗ

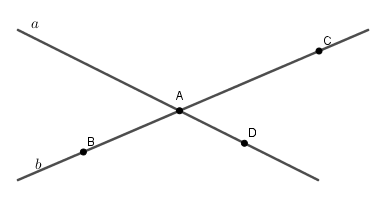
I. TRẮC NGHIỆM (2,0 điểm).

Hãy chọn duy nhất chỉ một chữ cái A, B, C, D đứng trước câu trả lời đúng và ghi vào tờ giấy thi.

Câu 1. Cho tập hợp \(M = \left\{ {9;3;0;5} \right\}\). Trong các tập hợp sau đây, tập nào là tập hợp con của \(M\)?

A. \(A = \left\{ {9;0;8} \right\}\)

B. \(B = \left\{ {7;0;5} \right\}\)

C. \(C = \emptyset \)

D. \(D = \left\{ {3;6} \right\}\)

Câu 2. Số nào sau đây chia hết cho cả \(2\) và \(9\)?

A. 32                           B. 42  

C. 52                           D. 162

Câu 3. Số nào sau đây không là số nguyên tố?

A. 19                           B. 57  

C. 11                           D. 17

Câu 4. Ước số chung lớn nhất của 45 và 15 là:

A. 15            B. 3           C. 5        D. 45

Câu 5. Sắp xếp các số nguyên \(3; - 8;7; - 4;0\) theo thứ tự tăng dần ta được:

A. \( - 4; - 8;0;3;7\)

B. \(7;3;0; - 4; - 8\)

C. \( - 8; - 4;0;3;7\)

D. \(7;3;0; - 8; - 4\)

Câu 6. Tổng của các số nguyên \(x\) thỏa mãn \( - 7 \le x \le 8\) là:

A. \(8\)                                    B. \(0\)

C. \( - 1\)                                 D. \(1\)

Câu 7. Cho \(AE = 3,5cm\), \(AD = 9cm\), \(DE = 5,5cm\). Khi đó

A. Ba điểm A, D, E không thẳng hàng

B. Điểm A nằm giữa D và E

C. Điểm E nằm giữa A và D

D. Điểm D nằm giữa A và E

Câu 8. Cho hình vẽ sau, khẳng định nào dưới đây là đúng?

A. Hai tia CA và CB đối nhau

B. Hai tia BA và AC trùng nhau

C. Hai tia AB và AD đối nhau

D. Hai tia BA và BC trùng nhau

II. TỰ LUẬN (8,0 điểm).

Bài 1. (2 điểm) Thực hiện phép tính (hợp lí nếu có thể)

a) \(136 + 172 + 64\)

b) \(130 - \left[ {49 - {{\left( {5 - 3} \right)}^2}} \right]\)

c) \(74 + \left( { - 39} \right) + \left( { - 45} \right) + \left| { - 39} \right|\)

d) \({7^3}{.5^2} + {76.7^3} - {7^6}:{7^3}\)

Bài 2. (2 điểm)  Tìm \(x\) biết: 

\(a)\,\,4x - 16 = 120:2\)

\(b)\,\,{64.2^{x - 2}} = {2^{2020}}\)

\(c)\,\,21 + 3\left| x \right| = 3.\left( {{4^2} - 1} \right)\)

\(d)\,\,12 \vdots x,80 \vdots x\) và \(x < 4\).

Bài 3. (1,5 điểm) Số học sinh khối 6 của một trường trong khoảng từ 300 đến 400 em. Khi xếp hàng 12, hàng 18, hàng 20 thì vừa đủ. Tính số học sinh khối 6 của trường đó?

Bài 4. (2 điểm) Trên tia Ox lấy hai điểm A và B sao cho \(OA = 2cm,OB = 5cm\).

a) Tính độ dài đoạn thẳng AB.

b) Gọi I là trung điểm của đoạn thẳng OA. Tính độ dài đoạn thẳng IA và IB.

c) Trên tia đối của tia Ox lấy điểm H sao cho \(OH = 5cm\). Hỏi điểm O có là trung điểm của đoạn thẳng HB không? Vì sao?

Bài 5. (0,5 điểm) Cho \(A = 4 + {4^2} + {4^3} + {4^4} + ... + {4^{89}}\). Tìm số dư khi chia \(A\) cho \(85\).

HẾT

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn Loigiaihay.com

PHẦN I: TRẮC NGHIỆM (2 điểm)

Câu 1 (NB):

Phương pháp:

Tập hợp A là con của B nếu mọi phần tử thuộc A đều thuộc B.

Cách giải:

Đáp án A: \(8 \notin M\) nên A sai.

Đáp án B: \(7 \notin M\) nên B sai.

Đáp án C: Tập \(\emptyset \) là con của mọi tập hợp nên C đúng.

Đáp án D: \(6 \notin M\) nên D sai.

Chọn C.

Câu 2 (NB):

Phương pháp:

Số có tận cùng là \(0,2,4,6,8\) thì chia hết cho \(2\).

Số có tổng các chữ số chia hết cho \(9\) thì chia hết cho \(9\).

Cách giải:

Trong các đáp án đã cho, số \(162\) chia hết cho \(2\) và \(162\) chia hết cho \(9\) vì \(1 + 6 + 2 = 9 \vdots 9\).

Chọn D.

Câu 3 (NB):

Phương pháp:

Sử dụng bảng số nguyên tố trong phạm vi \(100\).

Cách giải:

Số nguyên tố trong các đáp án đã cho là \(19,11,17\).

Số \(57\) là hợp số vì \(5 + 7 = 12 \vdots 3\) nên \(57 \vdots 3\).

Chọn B.

Câu 4 (TH):

Phương pháp:

Tìm ƯCLN của \(45\) và \(15\) bằng cách phân tích thành tích các thừa số nguyên tố.

Cách giải:

\(\begin{array}{l}45 = {3^2}.5\\15 = 3.5\end{array}\)

\( \Rightarrow UCLN\left( {45;15} \right) = 3.5 = 15\).

Chọn A.

Câu 5 (NB):

Phương pháp:

Chia các số nguyên thành hai nhóm, so sánh các số nguyên ở mỗi nhóm.

Cách giải:

Nhóm 1: \( - 8\) và \( - 4\), sắp xếp ta được \( - 8 <  - 4\).

Nhóm 2: \(3;7;0\), sắp xếp ta được \(0 < 3 < 7\).

Vậy sắp xếp theo thứ tự tăng dần ta được: \( - 8; - 4;0;3;7\).

Chọn C.

Câu 6 (TH):

Phương pháp:

Tìm các số nguyên \(x\) thỏa mãn bài toán và tính tổng.

Chú ý: Tổng hai số nguyên đối nhau bằng \(0\).

Cách giải:

Ta có: \( - 7 \le x \le 8\) nên \(x \in \left\{ { - 7; - 6; - 5;...;6;7;8} \right\}\).

Tổng các số nguyên trên là

\(\begin{array}{l}\left( { - 7} \right) + \left( { - 6} \right) + \left( { - 5} \right) + ... + 6 + 7 + 8\\ = \left[ {\left( { - 7} \right) + 7} \right] + \left[ {\left( { - 6} \right) + 6} \right] + ... + 0 + 8\\ = 0 + 0 + ... + 0 + 8\\ = 8\end{array}\)

Chọn A.

Câu 7 (NB):

Phương pháp:

Điểm \(M\) nằm giữa hai điểm \(A,B\) nếu \(AM + MB = AB\).

Cách giải:

Vì \(3,5 + 5,5 = 9\) nên \(AE + ED = AD\).

Vậy điểm E nằm giữa hai điểm A và D.

Chọn C.

Câu 8 (NB):

Phương pháp:

Sử dụng định nghĩa hai tia đối nhau, hai tia trùng nhau và kết luận.

Cách giải:

Đáp án A: sai vì hai tia CA và CB trùng nhau.

Đáp án B: sai vì hai tia BA và AC không chung gốc.

Đáp án C: sai vì ba điểm A, B, D không thẳng hàng.

Đáp án D: đúng vì hai tia BA và BC trùng nhau.

Chọn D.

PHẦN II. TỰ LUẬN (8,0 điểm).

Bài 1 (VD):

Phương pháp:

Nhóm các số hạng thích hợp để được tổng là số tròn trăm, tròn chục,…

Thứ tự thực hiện phép tính:

- Có ngoặc: trong ngoặc trước, ngoài ngoặc sau.

- Không có ngoặc: Lũy thừa, nhân chia, công trừ.

Cách giải:

a) \(136 + 172 + 64\)

\(\begin{array}{l} = \left( {136 + 64} \right) + 172\\ = 200 + 172\\ = 372\end{array}\)

b) \(130 - \left[ {49 - {{\left( {5 - 3} \right)}^2}} \right]\)

\(\begin{array}{l} = 130 - \left[ {49 - {2^2}} \right]\\ = 130 - \left[ {49 - 4} \right]\\ = 130 - 45\\ = 85\end{array}\)

c) \(74 + \left( { - 39} \right) + \left( { - 45} \right) + \left| { - 39} \right|\)

\(\begin{array}{l} = 74 + \left( { - 39} \right) + \left( { - 45} \right) + 39\\ = \left[ {74 + \left( { - 45} \right)} \right] + \left[ {\left( { - 39} \right) + 39} \right]\\ = 29 + 0\\ = 29\end{array}\)

d) \({7^3}{.5^2} + {76.7^3} - {7^6}:{7^3}\)

\(\begin{array}{l} = {7^3}.25 + {76.7^3} - {7^3}\\ = {7^3}\left( {25 + 76 - 1} \right)\\ = 343.100\\ = 34300\end{array}\)

Bài 2 (VD):

Phương pháp:

a) Sử dụng qui tắc chuyển vế đổi dấu.

b) Sử dụng so sánh \({a^n} = {a^m}\) thì \(n = m\).

c) Sử dụng qui tắc chuyển vế đổi dấu.

Chú ý: \(\left| x \right| = a > 0\) thì \(x = a\) hoặc \(x =  - a\).

d) Sử dụng định nghĩa ước chung.

Cách giải:

\(a)\,\,4x - 16 = 120:2\)

\(\begin{array}{l}4x - 16 = 60\\4x = 60 + 16\\4x = 76\\x = 76:4\\x = 19\end{array}\)

\(b)\,\,{64.2^{x - 2}} = {2^{2020}}\)

\(\begin{array}{l}{2^6}{.2^{x - 2}} = {2^{2020}}\\{2^{x - 2}} = {2^{2020}}:{2^6}\\{2^{x - 2}} = {2^{2014}}\\x - 2 = 2014\\x = 2014 + 2\\x = 2016\end{array}\)

\(c)\,\,21 + 3\left| x \right| = 3.\left( {{4^2} - 1} \right)\)

\(\begin{array}{l}21 + 3\left| x \right| = 3.\left( {16 - 1} \right)\\21 + 3\left| x \right| = 3.15\\21 + 3\left| x \right| = 45\\3\left| x \right| = 45 - 21\\3\left| x \right| = 24\\\left| x \right| = 8\end{array}\)

Vậy \(x = 8\) hoặc \(x =  - 8\).

d) \(12 \vdots x,80 \vdots x\)  và \(x < 4\)

\(12 \vdots x,80 \vdots x\)  nên \(x \in UC\left( {12;80} \right)\).

Ta có:

\(\begin{array}{l}12 = {2^2}.3\\80 = {2^4}.5\\ \Rightarrow UCLN\left( {12;80} \right) = {2^2} = 4\end{array}\)

\( \Rightarrow UC\left( {12;80} \right) = \left\{ {1;2;4} \right\}\)

Mà \(x < 4\) nên \(x \in \left\{ {1;2} \right\}\).

Vậy \(x \in \left\{ {1;2} \right\}\).

Bài 3 (VD):

Phương pháp:

Gọi số học sinh cần tìm là \(x\).

Lập luận tìm \(x\) từ các điều kiện bài cho, chú ý sử dụng kiến thức về bội chung.

Cách giải:

Gọi số học sinh cần tìm là \(x\) \(\left( {300 \le x \le 400,x \in \mathbb{N}} \right)\)

Vì xếp hàng 12, hàng 18, hàng 20 thì vừa đủ nên \(x \vdots 12,x \vdots 18,x \vdots 20\) hay \(x \in BC\left( {12;18;20} \right)\)

Ta có:

\(\begin{array}{l}12 = {2^2}.3\\18 = {2.3^2}\\20 = {2^2}.5\\ \Rightarrow BCNN\left( {12;18;20} \right) = {2^2}{.3^2}.5 = 180\end{array}\)

\( \Rightarrow BC\left( {12;18;20} \right) = \left\{ {0;180;360;540;...} \right\}\)

Mà \(300 \le x \le 400\) nên \(x = 360\).

Vậy khối 6 có \(360\) học sinh.

Bài 4 (VD):

Phương pháp:

Sử dụng các kiến thức:

Điểm M nằm giữa hai điểm A, B thì \(AM + MB = AB\)

Điểm M là trung điểm của đoạn thẳng AB thì \(MA = MB = \dfrac{{AB}}{2}\).

Cách giải:

a) Tính độ dài đoạn thẳng AB.

Trên tia \(Ox\), \(OA < OB\) (vì \(2cm < 5cm\)) nên điểm A nằm giữa hai điểm O và B

Ta có:

\(\begin{array}{l}OA + AB = OB\\2 + AB = 5\\AB = 5 - 2\\AB = 3\left( {cm} \right)\end{array}\)

Vậy \(AB = 3cm\).

b) Gọi I là trung điểm của đoạn thẳng OA. Tính độ dài đoạn thẳng IA và IB.

Vì \(I\) là trung điểm của \(OA\) nên \(OI = IA = \dfrac{{OA}}{2} = \dfrac{2}{2} = 1\left( {cm} \right)\).

Trên tia \(Ox\), \(OI < OB\left( {1cm < 5cm} \right)\) nên điểm I nằm giữa hai điểm O và B

Ta có:

\(\begin{array}{l}OI + IB = OB\\1 + IB = 5\\IB = 5 - 1\\IB = 4\left( {cm} \right)\end{array}\)

Vậy \(IA = 1cm,IB = 4cm\).

c) Trên tia đối của tia Ox lấy điểm H sao cho \(OH = 5cm\). Hỏi điểm O có là trung điểm của đoạn thẳng HB không? Vì sao?

Vì \(H,B\) nằm trên hai tia đối nhau gốc \(O\) nên điểm O nằm giữa hai điểm H và B.

Mà \(OH = 5cm,OB = 5cm\) nên \(OH = OB\left( { = 5cm} \right)\)

Vậy O là trung điểm của HB.

Bài 5 (VDC):

Phương pháp:

Nhóm 4 số hạng liền nhau thành một nhóm, nhận xét tính chất chia hết của các tổng đó với \(85\).

Cách giải:

\(A = 4 + {4^2} + {4^3} + {4^4} + ... + {4^{89}}\)

\( = \left( {4 + {4^2} + {4^3} + {4^4}} \right)\) \( + \left( {{4^5} + {4^6} + {4^7} + {4^8}} \right) + ...\) \( + \left( {{4^{85}} + {4^{86}} + {4^{87}} + {4^{88}}} \right) + {4^{89}}\)

\( = 4\left( {1 + 4 + {4^2} + {4^3}} \right)\) \( + {4^5}\left( {1 + 4 + {4^2} + {4^3}} \right) + ...\) \( + {4^{85}}\left( {1 + 4 + {4^2} + {4^3}} \right) + {4^{89}}\)

\( = 4.85 + {4^5}.85 + ... + {4^{85}}.85 + {4^{89}}\)

\( = 85\left( {4 + {4^5} + ... + {4^{85}}} \right) + {4^{89}}\)

Mà \(85 \vdots 85\) nên \(85\left( {4 + {4^5} + ... + {4^{85}}} \right) \vdots 85\)

Lại có:

\(\begin{array}{l}{4^4} \equiv 1\left( {\bmod \,85} \right)\\ \Rightarrow {\left( {{4^4}} \right)^{22}} \equiv 1\left( {\bmod \,85} \right)\\ \Rightarrow {4^{88}} \equiv 1\left( {\bmod \,85} \right)\\ \Rightarrow {4^{88}}.4 \equiv 4\left( {\bmod \,85} \right)\\ \Rightarrow {4^{89}} \equiv 4\left( {\bmod \,85} \right)\end{array}\)

Vậy số dư khi chia A cho 85 là 4.

HẾT

Loigiaihay.com