Tuần 24: Giới thiệu hình trụ. Giới thiệu hình cầu. Luyện tập chung - trang 26

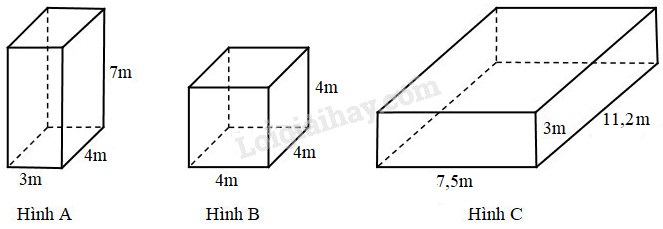
Bài 1

Tính diện tích xung quanh và diện tích toàn phần của các hình dưới đây: 

Phương pháp giải:

- Tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi đáy nhân với chiều cao.

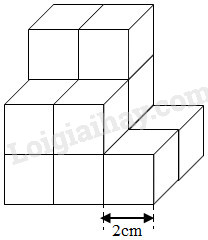
- Tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.

- Muốn tính diện tích xung quanh của hình lập phương ta lấy diện tích một mặt nhân với \(4\).

- Muốn tính diện tích toàn phần của hình lập phương ta lấy diện tích một mặt nhân với \(6\).

Lời giải chi tiết:

a) Hình A là hình hộp chữ nhật có chiều dài \(4m\), chiều rộng \(3m\) và chiều cao \(7m\).

Chu vi đáy của hình hộp chữ nhật là:

          \((3 + 4) \times 2 = 14\,\,(m)\)

Diện tích xung quanh của hình hộp chữ nhật là:

          \(14 \times 7 = 98\,\,({m^2})\)

Diện tích đáy của hình hộp chữ nhật là:

          \(4\times 3 = 12\,\,({m^2})\)

Diện tích toàn phần của hình hộp chữ nhật là:

          \(98 + 12 \times 2 = 122\,\,({m^2})\)

b)  Hình B là hình lập phương có độ dài cạnh là \(4m\).

Diện tích một mặt của hình lập phương đó là:

          \(4 \times 4 = 16\,\,({m^2})\)

Diện tích xung quanh của hình lập phương đó là:

          \(16\times 4 = 64\,\,({m^2})\)

Diện tích toàn phần của hình lập phương đó là:

          \(16 \times 6 = 96\,\,({m^2})\)

c) Hình C là hình hộp chữ nhật có chiều dài \(11,2m\), chiều rộng \(7,5m\) và chiều cao \(3m\).

Chu vi đáy của hình hộp chữ nhật là:

          \((11,2+ 7,5) \times 2 = 37,4\,\,(m)\)

Diện tích xung quanh của hình hộp chữ nhật là:

          \(37,4 \times 3 = 112,2\,\,({m^2})\)

Diện tích đáy của hình hộp chữ nhật là:

          \(11,2 \times 7,5 = 84\,\,({m^2})\)

Diện tích toàn phần của hình hộp chữ nhật là:

          \(112,2 + 84 \times 2 = 280,2\,\,({m^2})\)

Bài 2

Tính thể tích các hình ở bài 1 rồi viết kết quả vào chỗ chấm:

a) Hình A có thể tích là: ……..

b) Hình B có thể tích là: ……..

c) Hình C có thể tích là: ……..

Phương pháp giải:

- Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng đơn vị đo).

- Muốn tính thể tích hình lập phương ta lấy cạnh nhân với cạnh rồi nhân với cạnh.

Lời giải chi tiết:

Thể tích hình A là:

           \(4 \times 3 \times 7 = 84\,\,({m^3})\)

Thể tích hình B là:

          \(4 \times 4 \times 4 = 64\,\,({m^3})\)

Thể tích hình C là:

          \(11,2 \times 7,5 \times 3 = 252\,\,({m^3})\)    

Vậy:

a) Hình A có thể tích là \(84{m^3}\).

b) Hình B có thể tích là \(64{m^3}\).

c) Hình C có thể tích là \(252{m^3}\).

Bài 3

Viết vào chỗ chấm cho thích hợp:

a) 10% của 260 là ……..

     5% của 260 là ……..

     Vậy 15% của 260 là ……..

b) 10% của 780 là ……..

     ……..% của 780 là ……..

     ……..% của 780 là ……..

     ……..% của 780 là ……..

     Vậy: 23,5% của 780 là: ……..

Phương pháp giải:

Áp dụng công thức:

\(A\%  + B\%  = (A + B)\% ;\) \(A\% :n = (A:n)\% \)

Lời giải chi tiết:

a)  10% của 260 là 26.

     5% của 260 là 13.

Vậy 15% của 260 là 39.

b)  10% của 780 là 78.

      20% của 780 là 156.

      3% của 780 là 23,4.

      0,5% của 780 là 3,9

Vậy 23,5% của 780 là 183,3.

Bài 4

Khối gỗ bên được ghép bởi 12 hình lập phương nhỏ có cạnh 2cm. Tính thể tích khối gỗ. 

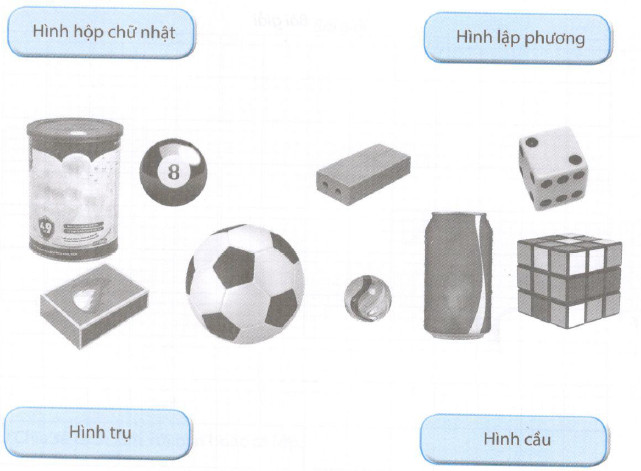
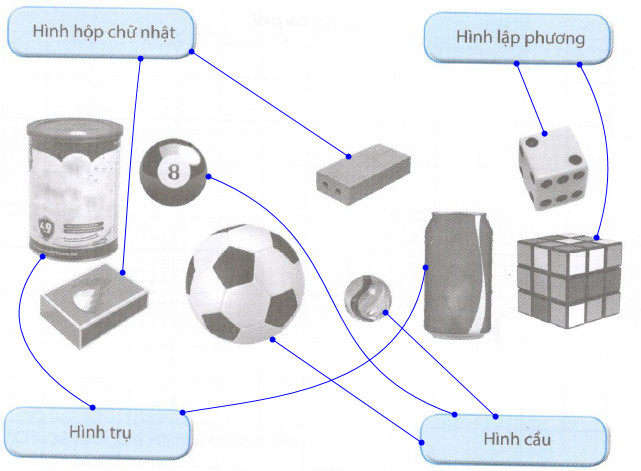
Phương pháp giải:

- Tính thể tích một khối lập phương nhỏ cạnh \(2cm\) ta lấy cạnh nhân với cạnh rồi nhân với cạnh.

- Tính thể tích khối gỗ ta thể tích một khối lập phương nhỏ cạnh \(2cm\) nhân với \(12\) (vì khối gỗ được ghép bởi \(12\) hình lập phương nhỏ).

Lời giải chi tiết:

Thể tích một khối lập phương nhỏ cạnh \(2cm\) là:

             \(2 \times 2 \times 2 = 8\,\,(c{m^3})\)

Thể tích khối gỗ đó là:

             \(8 \times 12 = 96\,\,(c{m^3})\)

Vậy thể tích khối gỗ đó là \(96c{m^3}\).

Bài 5

Nối mỗi đồ vật với tên hình thích hợp: 

Phương pháp giải:

Quan sát kĩ các hình vẽ đã cho để xác định hình dạng của các đồ vật đã cho.

Lời giải chi tiết:

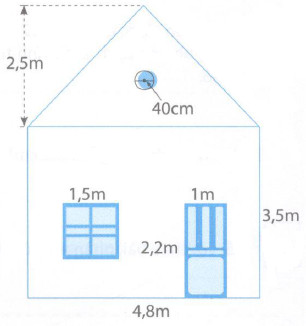
Bài 6

Người ta muốn sơn một bức tường có kích thước như hình vẽ bên. Tính diện tích cần sơn (không sơn cửa, cửa sổ và ô thoáng)

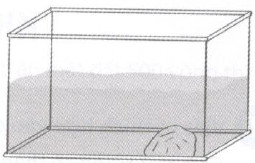
Phương pháp giải:

- Áp dụng các công thức tính diện tích:

Diện tích hình tròn = bán kính × bán kính × 3,14;

Diện tích hình vuông = cạnh × cạnh;

Diện tích hình chữ nhật =  chiều dài × chiều rộng;

Diện tích hình tam giác = độ dài đáy × chiều cao : 2.

- Diện tích cần sơn = diện tích cả bức tường – (diện tích cửa + diện tích cửa sổ + diện tích ô thoáng).

Lời giải chi tiết:

Đổi \(40cm = 0,4m\)

Diện tích bức tường hình tam giác (kể cả ô thoáng) là:

           \(4,8 \times 2,5:2 = 6\,\,({m^2})\)

Diện tích bức tường hình chữ nhật (kể cả cửa và cửa sổ) là:

           \(4,8 \times 3,5 = 16,8\,\,({m^2})\)

Diện tích cả bức tường đó là:

           \(6 + 16,8 = 22,8\,\,({m^2})\)

Bán kính ô thoáng là:

           \(0,4:2 = 0,2\,\,(m)\)

Diện tích ô thoáng là:

       \(0,2 \times 0,2 \times 3,14 = 0,1256\,\,({m^2})\)

Diện tích cửa sổ là:

            \(1,5 \times 1,5 = 2,25\,\,({m^2})\)

Diện tích cửa là:

          \(2,2 \times 1 = 2,2\,\,({m^2})\)

Diện tích cần sơn là:

\(22,8\, - (2,2 + 2,25 + 0,1256)\)\( = 18,2244\,\,({m^2})\)

                              Đáp số: \(18,2244\,{m^2}\).

Bài 7

Một mảnh vườn hình thang vuông có đáy lớn là 30m, đáy bé 20m, chiều cao 15m. Người ta đào một cái ao hình vuông cạnh 15m sát phần góc vuông của hình thang, phần còn lại làm vườn rau.

a) Tính diện tích ao, diện tích vườn rau.

b) Tính tỉ số phần trăm diện tích ao và diện tích vườn rau.

Phương pháp giải:

- Tính diện tích mảnh vườn hình thang ta lấy tổng độ dài hai đáy chia cho \(2\).

- Tính diện tích ao ta lấy cạnh nhân với cạnh.

- Tính diện tích vườn rau ta lấy diện tích mảnh vườn trừ đi diện tích ao.

- Tính tỉ số phần trăm của diện tích ao và diện tích vườn rau ta tìm thương của diện tích ao và diện tích vườn rau, sau đó nhân thương đó với 100 và viết thêm kí hiệu % vào bên phải tích tìm được.

Lời giải chi tiết:

a) Diện tích mảnh vườn hình thang đó là:

             \((30 + 20) \times 15:2 = 375\,\,({m^2})\)

Diện tích ao là:

             \(15 \times 15 = 225\,\,({m^2})\)

Diện tích vườn rau là:

             \(375 - 225 = 150\,\,({m^2})\)

b) Tỉ số phần trăm diện tích ao và diện tích vườn rau là:

               \(225:150 = 1,5 = 150\% \)

            Đáp số: a) Diện tích ao: \(225{m^2}\);

                       Diện tích vườn rau: \(150{m^2}\).

                        b) \(150\% \).

Bài 8

Một bể cá thủy tinh dạng hình hộp chữ nhật có chiều dài 50cm, chiều rộng 30cm, mực nước trong bể cao 5cm. Sau khi thả một viên đá vào bể thì mực nước trong bể cao 7cm. Tính thể tích viên đá, biết rằng viên đá chìm hoàn toàn trong nước.

Phương pháp giải:

- Tính thể tích nước ban đầu trong bể (bằng thể tích của hình hộp chữ nhật có chiều dài 50cm, chiều rộng 30cm, chiều cao 5cm).

- Tính thể tích sau khi thả viên đá vào (bằng thể tích của hình hộp chữ nhật có chiều dài 50cm, chiều rộng 30cm, chiều cao 7cm).

- Tính thể tích viên đá ta lấy thể tích sau khi thả viên đá vào trừ đi thể tích nước ban đầu trong bể.

Lời giải chi tiết:

Thể tích nước ban đầu trong bể là:

           \(50 \times 30 \times 5 = 7500\,\,(c{m^3})\)

Thể tích sau khi thả viên đá vào là:

           \(50 \times 30 \times 7 = 10500\,\,(c{m^3})\)

Thể tích viên đá là:

            \(10500 - 7500 = 3000\,\,(c{m^3})\)

                                   Đáp số:  \(3000c{m^3}\).

Vui học

Một hộp thuốc hình hộp chữ nhật, kích thước như hình vẽ.

a) Tính diện tích bìa dùng làm chiếc hộp đó, biết các mép gấp có diện tích 20cm². 

b) Tính thể tích chiếc hộp thuốc đó.

Phương pháp giải:

Diện tích bìa dùng làm chiếc hộp đó bằng diện tích toàn phần của cái hộp cộng với diện tích mép gấp.

Lời giải chi tiết:

Hộp thuốc hình hộp chữ nhật đã cho có chiều dài 5cm, chiều rộng 4cm và chiều cao 8cm.

 a) Diện tích xung quanh của hộp thuốc đó là:

            \((5 + 4) \times 2 \times 8 = 144\,\,(c{m^2})\) 

Diện tích đáy của hộp thuốc đó là:

            \(5 \times 4 = 20\,\,(c{m^2})\)

Diện tích toàn phần của hộp thuốc đó là:

            \(144 + 20 \times 2 = 184\,\,(c{m^2})\)

Diện tích bìa dùng làm chiếc hộp đó là:

             \(184 + 20 = 204\,\,(c{m^2})\)

b) Thể tích chiếc hộp thuốc đó là:

             \(5 \times 4 \times 8 = 160\,\,(c{m^3})\)

                       Đáp số: a) \(204c{m^2}\);

                                   b) \(160c{m^3}\). 

Loigiaihay.com