Giải câu hỏi trắc nghiệm trang 69 vở thực hành Toán 8

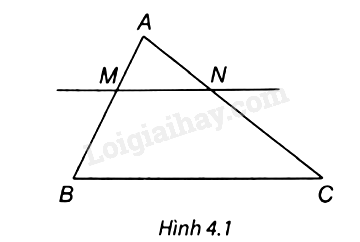
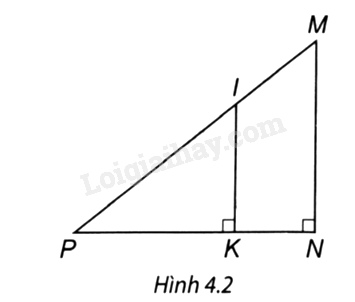
Câu 1 trang 69

Quan sát Hình 4.1 biết MN // BC. Tỉ số \(\frac{{AM}}{{MB}}\) bằng

A. \(\frac{{AN}}{{AC}}\)

B. \(\frac{{AN}}{{NC}}\)

C. \(\frac{{NC}}{{AN}}\)

D. \(\frac{{BM}}{{AB}}\)

Phương pháp giải:

Áp dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh cong lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Lời giải chi tiết:

Áp dụng định lí Thalès, MN // BC \( \Rightarrow \frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}.\)

=> Chọn đáp án B.

Câu 2 trang 69

Quan sát Hình 4.2 và chọn khẳng định đúng.

A. \(\frac{{PI}}{{PM}} = \frac{{KN}}{{PN}}.\)

B. \(\frac{{IM}}{{IP}} = \frac{{KP}}{{PN}}.\)

C. \(\frac{{MI}}{{MP}} = \frac{{NK}}{{NP}}.\)

D. \(\frac{{PI}}{{PM}} = \frac{{PK}}{{KN}}.\)

Phương pháp giải:

Áp dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh cong lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Lời giải chi tiết:

Ta có IK ⊥ PN, MN ⊥ PN ⇒ IK // MN.

Áp dụng định lí Thales, ta có: \(\frac{{PI}}{{PM}} = \frac{{PK}}{{PN}};\,\,\frac{{MI}}{{MP}} = \frac{{NK}}{{NP}}.\)

=> Chọn đáp án C.

Câu 3 trang 70

Cho AB = 10 cm; MN = 3 dm. Tỉ số nào đúng?

A. \(\frac{{AB}}{{MN}} = \frac{{10}}{3}.\)

B. \(\frac{{AB}}{{MN}} = \frac{3}{{10}}.\)

C. \(\frac{{AB}}{{MN}} = \frac{1}{3}.\)

D. \(\frac{{AB}}{{MN}} = 3.\)

Phương pháp giải:

Dựa vào tỉ số hai đoạn thẳng: Tỉ số hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.

Lời giải chi tiết:

Đổi 3 dm = 10 cm

Do đó \(\frac{{AB}}{{MN}} = \frac{{10}}{{30}} = \frac{1}{3}.\)

=> Chọn đáp án C.

Câu 4 trang 70

Quan sát Hình 4.3. Biết DE // BC, AD = 12, DB = 18, CE = 30. Độ dài AC bằng:

A. 20.

B. 56.

C. 45.

D. 50.

Phương pháp giải:

Áp dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh cong lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Lời giải chi tiết:

Áp dụng định lí Thales, ta có: \(\frac{{DB}}{{AB}} = \frac{{CE}}{{AC}}\) Mà AB = AD + DB = 12 + 18 = 30

Khi đó \(\frac{{18}}{{30}} = \frac{{30}}{{AC}} \Rightarrow AC = 30:\frac{{18}}{{30}} = 50.\)

Do đó AC = 50.

=> Chọn đáp án D.

Câu 5 trang 70

Cho tam giác ABC, đường thẳng d song song với BC cắt 2 cạnh AB và AC lần lượt tại M và N. Biết rằng \(\frac{{AM}}{{MB}} = \frac{1}{2}.\) Tính tỉ số chu vi tam giác AMN và ABC?

A. \(\frac{1}{3}.\)

B. \(\frac{2}{3}.\)

C. \(\frac{1}{2}.\)

D. \(\frac{1}{4}.\)

Phương pháp giải:

Áp dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh cong lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Lời giải chi tiết:

Tỉ số chu vi tam giác AMN và tam giác ABC là: \(\frac{{AM + AN + MN}}{{AB + AC + BC}}.\)

Áp dụng định lí Thales, ta có: \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) mà \(\frac{{AM}}{{MB}} = \frac{1}{2}\).

Do đó \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{3}.\) Áp dụng dãy tỉ số bằng nhau, suy ra \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{3} = \frac{{AM + AN + MN}}{{AB + AC + BC}}.\)

=> Chọn đáp án A.