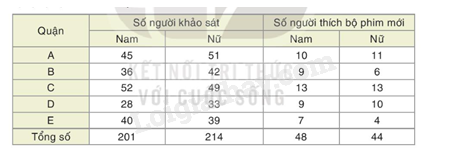
Giải bài 9 trang 80 vở thực hành Toán 8 tập 2Bảng sau đây thống kê kết quả khảo sát số người thích một bộ phim mới tại 5 quận A, B, C, D, E của thành phố X Quảng cáo
Đề bài Bảng sau đây thống kê kết quả khảo sát số người thích một bộ phim mới tại 5 quận A, B, C, D, E của thành phố X a) Chọn ngẫu nhiên một người ở quận C. Ước lượng xác suất của biến cố: A: "Người được chọn thích bộ phim đó" b) Chọn ngẫu nhiên một người ở quận E. Ước lượng xác suất của biến cố: B: "Người được chọn không thích bộ phim đó" c) Chọn ngẫu nhiên 600 người ở thành phố X. Ước lượng trong đó có bao nhiêu người thích bộ phim đó d) Chọn ngẫu nhiên 500 người nữ ở thành phố X. Ước lượng trong đó có bao nhiêu người thích bộ phim đó? Phương pháp giải - Xem chi tiết Tính xác suất của biến cố A, B từ đó ước lượng số người thích bộ phim đó. Lời giải chi tiết a) Số người ở quận C được khảo sát là 52 + 49 = 101 người, trong đó có 13 + 13 = 6 người thích bộ phim. Vậy xác suất của biến cố A được ước lượng là \(\frac{{26}}{{101}}\). b) Số người ở quận E được khảo sát là 40 + 39 = 79 người, trong đó có 7 + 4 = 11 người thích bộ phim. Do đó, có 79 – 11 = 68 người không thích bộ phim.Vậy xác suất của biến cố B được ước lượng là \(\frac{{68}}{{79}}\). c) Gọi C là biến cố “Người được chọn thích bộ phim đó”. Số người ở thành phố X được khảo sát là 201 + 214 = 415 người, trpmg đps cps 48 + 44 = 92 người thích bộ phim. Vậy xác suất của biến cố C được ước lượng P(C) \( \approx \frac{{92}}{{415}}\). Gọi k là người thích bộ phim. Ta có: P(C) \( \approx \frac{k}{{600}}\). Thay giá trị ước lượng của P(C), ta được \(\frac{k}{{600}} \approx \frac{{92}}{{415}}\), suy ra k \( \approx \frac{{92.600}}{{415}} = 133\). Vậy ta ước lượng có khoảng 133 người thích bộ phim đó trong số 600 người của thành phố X. d) Gọi D là biến cố “Người nữ được chọn thích bộ phim đó”. Số người nữ ở thành phố X được khảo sát là 214 người, trong đó có 44 người thích bộ phim. Vậy xác suất của biến cố D được ước lượng là P(D) \( \approx \frac{{44}}{{214}}\). Gọi h là người thích bộ phim. Ta có P(D) \( \approx \frac{h}{{500}}\). Thay giá trị ước lượng ucar P(D), ta được \(\frac{h}{{500}} \approx \frac{{44}}{{214}}\), suy ra h \( \approx \frac{{44.500}}{{214}} = 103\). Vậy ta ước lượng có khoảng 103 người thích bộ phim đó trong số 500 người nữ của thành phố X.
|




















Danh sách bình luận