Giải bài 7 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạoCho tam giác đều tâm O. Hỏi có bao nhiêu phép quay tâm O với góc quay \(\alpha \), \(0{\rm{ }} < {\rm{ }}\alpha {\rm{ }} \le {\rm{ }}2\pi ,\)biến tam giác trên thành chính nó? Quảng cáo
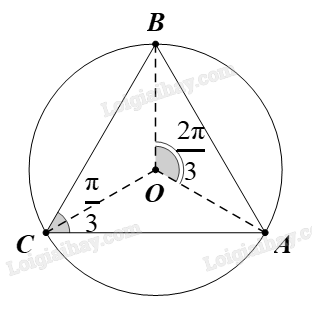
Đề bài Cho tam giác đều tâm O. Hỏi có bao nhiêu phép quay tâm O với góc quay \(\alpha \), \(0{\rm{ }} < {\rm{ }}\alpha {\rm{ }} \le {\rm{ }}2\pi ,\)biến tam giác trên thành chính nó? A. Một. B. Hai. C. Ba. D. Bốn. Phương pháp giải - Xem chi tiết Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay. Lời giải chi tiết Đáp án đúng là: C Gọi tam giác đã cho là ∆ABC. ⦁ \(\Delta \)ABC đều có tâm O. Suy ra \(OA{\rm{ }} = {\rm{ }}OB{\rm{ }} = {\rm{ }}OC\) và \(\widehat {ACB} = \frac{\pi }{3}\) Khi đó \(\widehat {AOB} = 2\widehat {ACB} = 2.\frac{\pi }{3} = \frac{{2\pi }}{3}\) Chứng minh tương tự, ta được \(\widehat {BOC} = \widehat {COA} = \frac{{2\pi }}{3}\) Vì vậy phép quay tâm O, góc quay \(\alpha = \frac{{2\pi }}{3}\) biến các điểm A, B, C theo thứ tự thành các điểm B, C, A. Do đó phép quay tâm O, góc quay \(\alpha = \frac{{2\pi }}{3}\) biến \(\Delta \)ABC thành chính nó. ⦁ Tương tự ta có phép quay tâm O, góc quay \(\alpha = \frac{{4\pi }}{3}\) biến các điểm A, B, C theo thứ tự thành các điểm C, A, B. Do đó phép quay tâm O, góc quay \(\alpha = \frac{{4\pi }}{3}\) biến \(\Delta \)ABC thành chính nó. ⦁ Phép quay tâm O, góc quay \(\alpha = \frac{{4\pi }}{3}\) biến các điểm A, B, C theo thứ tự thành các điểm A, B, C. Do đó phép quay tâm O, góc quay \(\alpha {\rm{ }} = {\rm{ }}2\pi \;\) biến ∆ABC thành chính nó. Vậy có 3 phép quay tâm O với các góc quay lần lượt là \(\alpha = \frac{{2\pi }}{3}\); \(\alpha = \frac{{4\pi }}{3}\); \(\alpha {\rm{ }} = {\rm{ }}2\pi \;\)thỏa mãn yêu cầu bài toán. Do đó ta chọn phương án C.
|




















Danh sách bình luận