Giải bài 6.6 trang 8 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

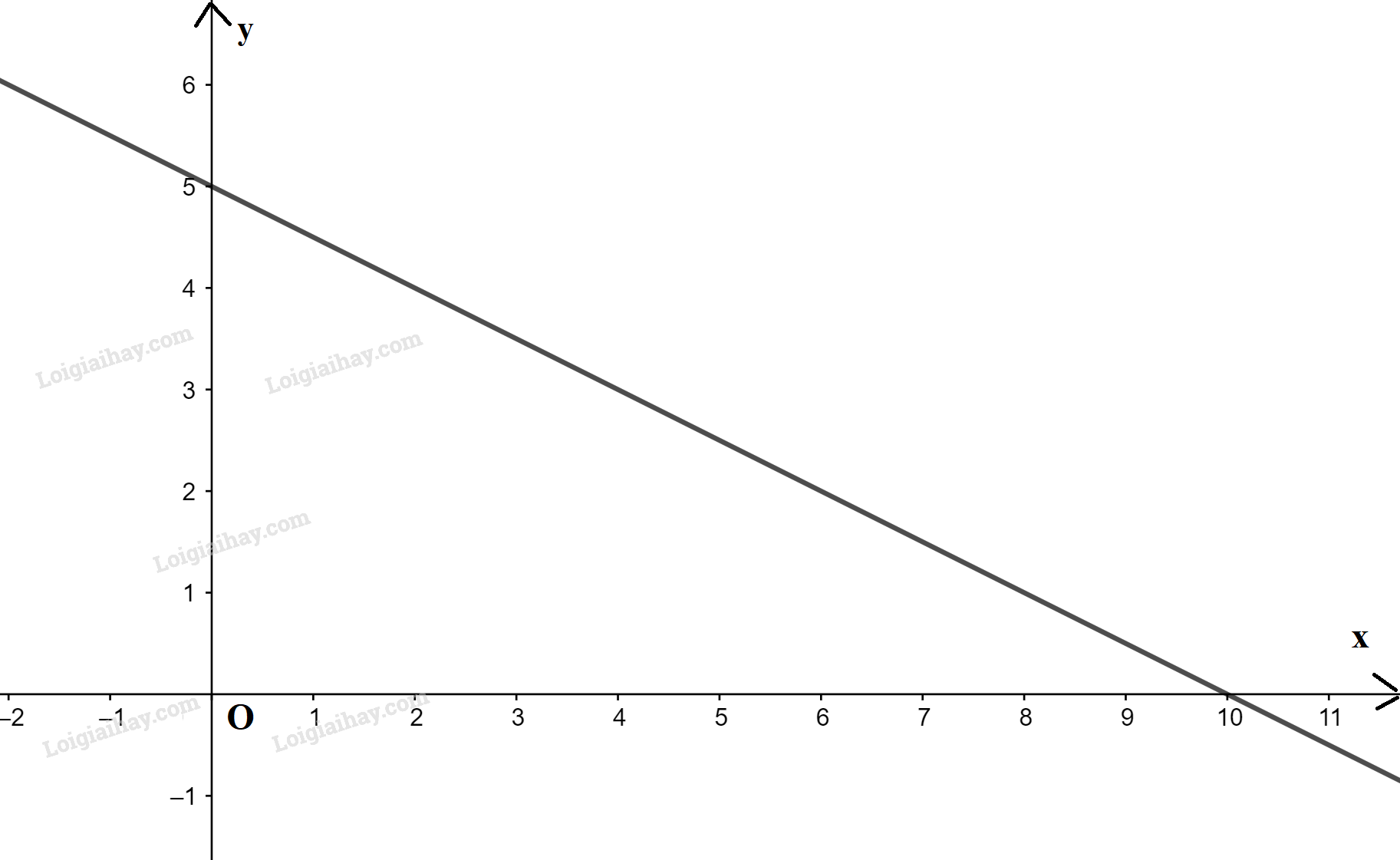
Đề bài

Vẽ đồ thị của các hàm số sau và chỉ ra tập giá trị, các khoảng đồng biến, nghịch biến của chúng

a) \(y =  - \frac{1}{2}x + 5\)   

b) \(y = 3{x^2}\)

c) \(y = \left\{ \begin{array}{l}{x^2},x \ge 0\\ - x - 1,x < 0\end{array} \right.\)

Lời giải chi tiết

a) \(y =  - \frac{1}{2}x + 5\)

Đồ thị hàm số \(y =  - \frac{1}{2}x + 5\) là đường thẳng đi qua 2 điểm A(0; 5) và B\(\left( {10;0} \right)\)

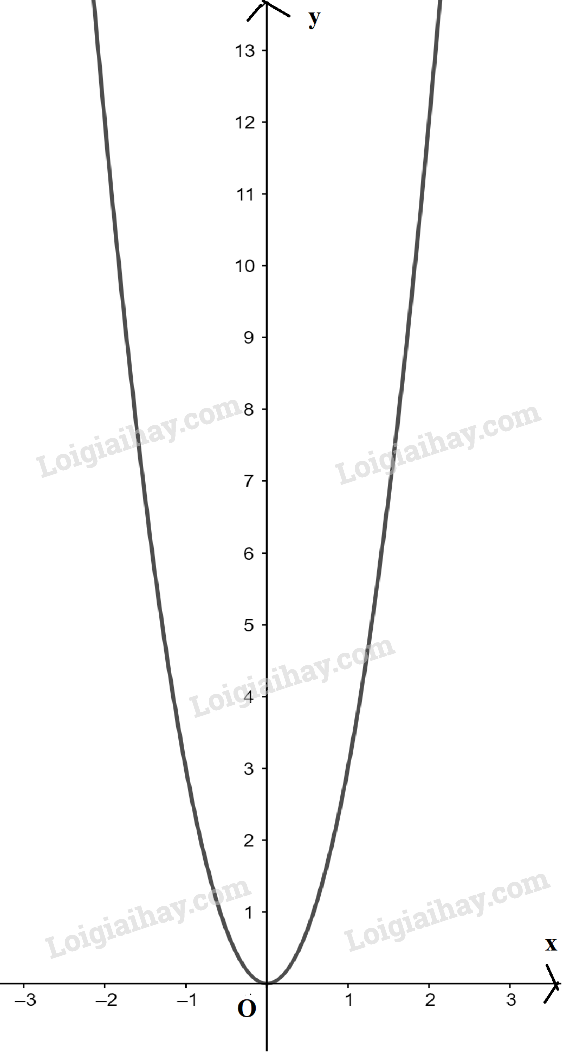
Từ đồ thị ta có:

  +) Tập giá trị: \(\mathbb{R}\)

  +) Hàm số nghịch biến trên \(\mathbb{R}\)

b) \(y = 3{x^2}\)

Đồ thị hàm số \(y = 3{x^2}\) là đường parabol có bề lõm quay lên trên và đỉnh là gốc tọa độ O

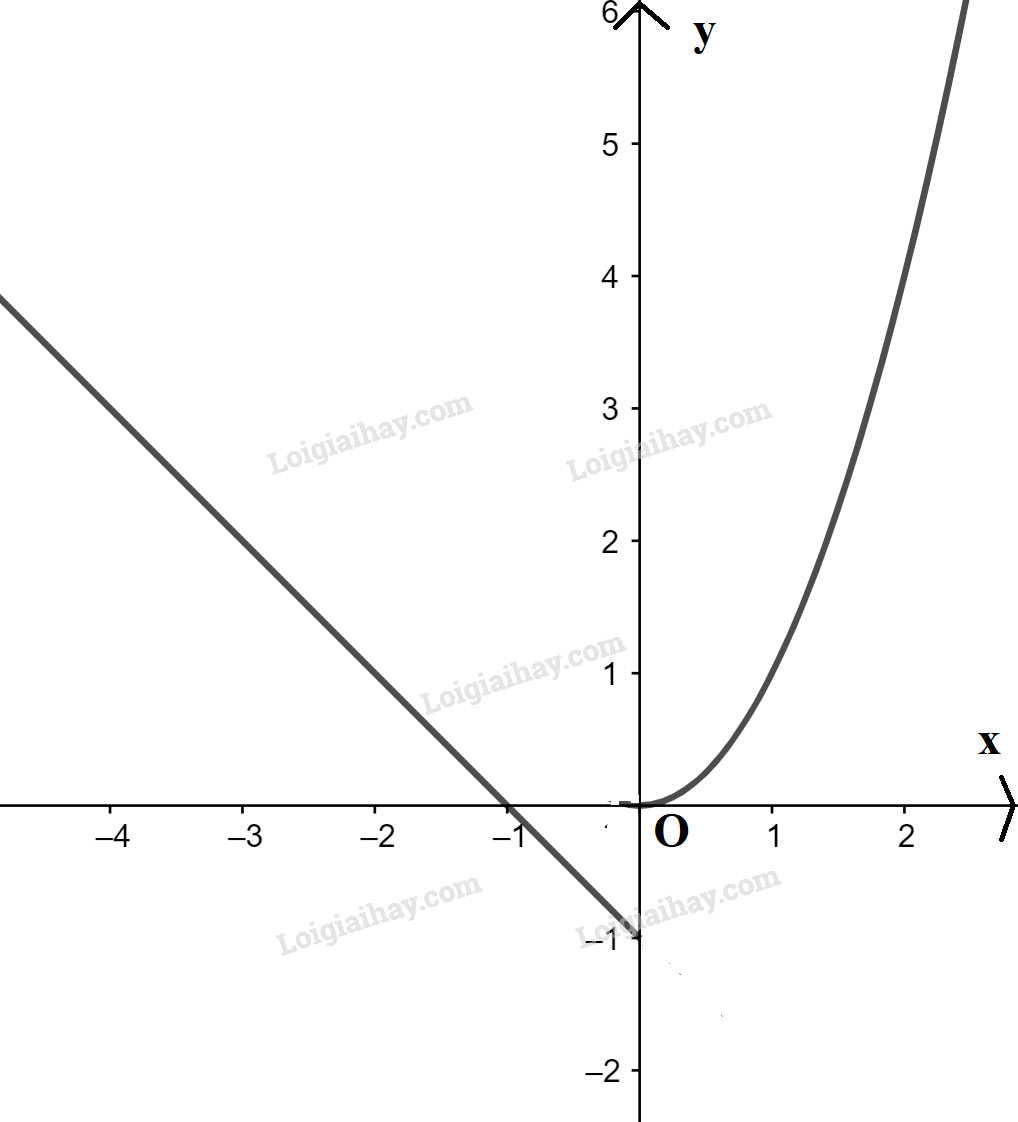
Từ đồ thị ta có:

+) Tập giá trị: \({\rm{[}}0; + \infty )\)

+) Hàm số nghịch biến trên \(( - \infty ;0)\) và đồng biến trên \((0; + \infty )\)

c) \(y = \left\{ \begin{array}{l}{x^2},x \ge 0\\ - x - 1,x < 0\end{array} \right.\)

Ta có đồ thị sau:

Từ đồ thị ta có:

+) Tập giá trị: \(( - 1; + \infty )\)

+) Hàm số nghịch biến trên \(( - \infty ;0)\) và đồng biến trên \((0; + \infty )\)