Giải bài 6.59 trang 26 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

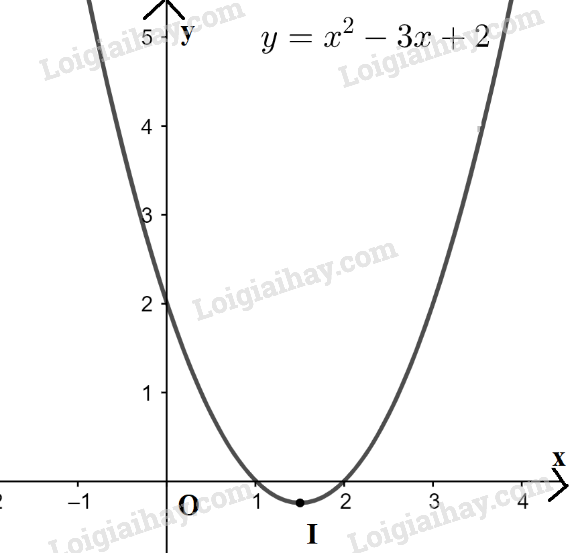
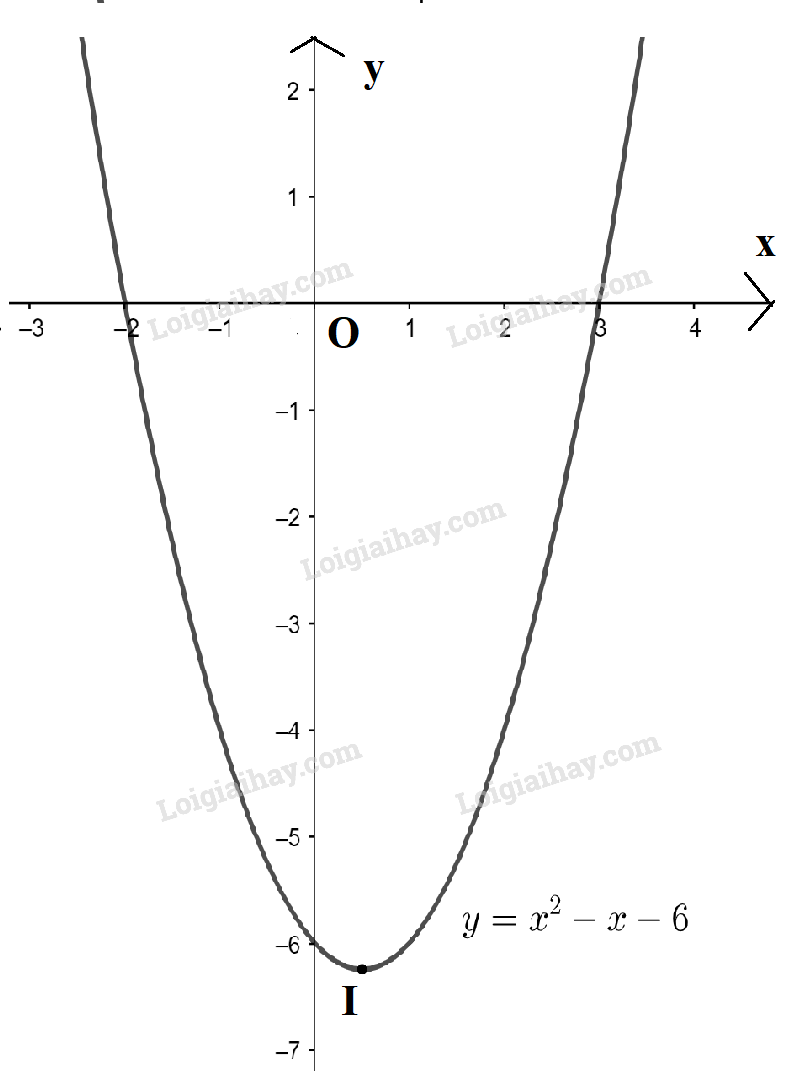
Đề bài

Vẽ đồ thị mỗi hàm số sau, từ đó suy ra tập nghiệm của bất phương trình tương ứng

a) \(y = {x^2} - 3x + 2\) và bất phương trình \({x^2} - 3x + 2 \ge 0\)

b) \(y = {x^2} - x - 6\) và bất phương trình \({x^2} - x - 6 < 0\)

Lời giải chi tiết

a) \(y = {x^2} - 3x + 2\) và bất phương trình \({x^2} - 3x + 2 \ge 0\)

+) Vẽ đồ thị

Ta có: a = 1 > 0 nên parabol có bề lõm quay lên trên. Đỉnh \(I\left( {\frac{3}{2}; - \frac{1}{4}} \right)\). Trục đối xứng \(x = \frac{3}{2}\)

Giao điểm của đồ thị với trục Oy là (0 ; 2) và đồ thị cắt trục Ox tại 2 điểm có hoành độ là x = 1 và x = 2

+) Giải BPT \({x^2} - 3x + 2 \ge 0\)

Từ đồ thị ta thấy với x ≤ 1 hoặc x ≥ 2 thì đồ thị hàm số \(y = {x^2} - 3x + 2\) nằm phía trên trục hoành.

Vậy tập nghiệm của BPT \({x^2} - 3x + 2 \ge 0\) là \(( - \infty ;1] \cup {\rm{[}}2; + \infty )\)

b) \(y = {x^2} - x - 6\) và bất phương trình \({x^2} - x - 6 < 0\)

+) Vẽ đồ thị

Ta có: a = 1 > 0 nên parabol có bề lõm quay lên trên. Đỉnh \(I\left( {\frac{1}{2}; - \frac{{25}}{4}} \right)\). Trục đối xứng \(x = \frac{1}{2}\)

Giao điểm của đồ thị với trục Oy là (0 ; -6) và đồ thị cắt trục Ox tại 2 điểm có hoành độ là x = 3 và x = -2

+) Giải BPT \({x^2} - x - 6 < 0\)

Từ đồ thị ta thấy với -2 < x < 3 thì đồ thị hàm số \(y = {x^2} - x - 6\) nằm phía dưới trục hoành.

Vậy tập nghiệm của BPT \({x^2} - x - 6 < 0\) là \(( - 2;3)\)