Giải bài 59 trang 119 sách bài tập toán 11 - Cánh diềuCho hình lập phương \(ABCD.A'B'C'D'\) có \(AB = a\). Quảng cáo
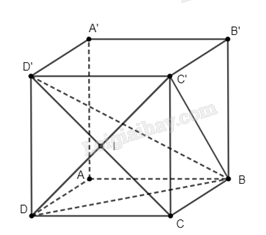
Đề bài Cho hình lập phương \(ABCD.A'B'C'D'\) có \(AB = a\). a) Chứng minh răng \(C'D \bot \left( {BCD'} \right)\), \(BD' \bot C'D\) và \(\left( {BC'D} \right) \bot \left( {BCD'} \right)\). b) Tính góc giữa hai đường thẳng \(BD\) và \(A'D'\). c) Tính góc giữa đường thẳng \(BD\) và mặt phẳng \(\left( {CDD'C'} \right)\). d) Tính số đo của góc nhị diện \(\left[ {B,DD',C} \right]\). e) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {BCD'} \right)\). g) Chứng minh \(B'C'\parallel \left( {BCD'} \right)\) và tính khoảng cách giữa đường thẳng \(B'C'\) và mặt phẳng \(\left( {BCD'} \right)\). h) Tính thể tích của khối tứ diện \(C'BCD\) và tính khoảng cách từ điểm \(C\) đến mặt phẳng \(\left( {BC'D} \right)\). Phương pháp giải - Xem chi tiết a) Để chứng minh đường thẳng vuông góc với mặt phẳng, ta chứng minh đường thẳng đó vuông góc với 2 đường thẳng bất kỳ cắt nhau trong mặt phẳng. Để chứng minh 2 mặt phẳng vuông góc, ta cần chỉ là 1 đường thẳng nằm trên mặt phẳng này và vuông góc với mặt phẳng kia. b) Chỉ ra \(AD\parallel A'D'\), nên góc giữa \(BD\) và \(A'D'\) cũng bằng góc giữa \(BD\) và \(AD\), và bằng \(\widehat {ADB}\). c) Ta chứng minh \(BC \bot \left( {DCC'D'} \right)\), do đó góc giữa đường thẳng \(BD\) và mặt phẳng \(\left( {DCC'D'} \right)\) là góc \(\widehat {BDC}\). d) Ta chứng minh \(\widehat {BDC}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,DD',C} \right]\). e) Gọi \(I\) là giao điểm của \(D'C\) và \(DC'\). Theo câu a, ta có \(DI \bot \left( {BCD'} \right)\), từ đó suy ra khoảng cách từ \(D\) đến \(\left( {BCD'} \right)\) là đoạn thẳng \(DI\). g) Để chứng minh \(B'C'\parallel \left( {BCD'} \right)\), ta chứng minh \(B'C'\) song song với một đường thẳng trong mặt phẳng \(\left( {BCD'} \right)\). Do \(B'C'\parallel \left( {BCD'} \right)\) nên khoảng cách giữa \(B'C'\) và \(\left( {BCD'} \right)\) bằng khoảng cách từ \(C'\) đến \(\left( {BCD'} \right)\). Theo câu a, ta có \(IC' \bot \left( {BCD'} \right)\), từ đó suy ra \(C'I\) chính là khoảng cách cần tìm. h) Công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\), với \(S\) là diện tích đáy và \(h\) là chiều cao của khối chóp đó. Do \(CC' \bot \left( {BCD} \right)\) nên thể tích tứ diện \(C'BCD\) là \(V = \frac{1}{3}CC'.{S_{BCD}}\). Do thể tích tứ diện \(C'BCD\) cũng có thể được tính bằng công thức \(V = \frac{1}{3}{d_{C,\left( {BC'D} \right)}}.{S_{BC'D}}\), ta suy ra \({d_{C,\left( {BC'D} \right)}} = \frac{{3V}}{{{S_{BC'D}}}}\). Lời giải chi tiết
a) Do \(ABCD.A'B'C'D'\) là hình lập phương, nên ta có \(BC \bot \left( {DCC'D'} \right)\), điều này suy ra \(BC \bot C'D\). Vì \(DCC'D'\) là hình vuông, nên ta có \(C'D \bot CD'\). Vậy ta có \(BC \bot C'D\), \(C'D \bot CD'\) nên ta có \(C'D \bot \left( {BCD'} \right)\). Ta có điều phải chứng minh. Do \(C'D \bot \left( {BCD'} \right)\), ta suy ra \(BD' \bot C'D\). Do \(C'D \bot \left( {BCD'} \right)\), mà \(C'D \subset \left( {BC'D} \right)\),ta suy ra \(\left( {BC'D} \right) \bot \left( {BCD'} \right)\). b) Dễ thấy rằng do \(ABCD.A'B'C'D'\) là hình lập phương, ta có \(AD\parallel A'D'\), nên góc giữa \(BD\) và \(A'D'\) cũng bằng góc giữa \(BD\) và \(AD\), và bằng \(\widehat {ADB}\). Do \(ABCD\) là hình vuông, nên \(\widehat {ADB} = {45^o}\). Vậy góc giữa \(BD\) và \(A'D'\) bằng \({45^o}\). c) Do \(ABCD.A'B'C'D'\) là hình lập phương, nên ta có \(BC \bot \left( {DCC'D'} \right)\). Điều này suy ra \(C\) là hình chiếu của \(B\) trên \(\left( {DCC'D'} \right)\). Như vậy, góc giữa đường thẳng \(BD\) và mặt phẳng \(\left( {DCC'D'} \right)\) là góc \(\widehat {BDC}\). Do \(ABCD\) là hình vuông, nên \(\widehat {BDC} = {45^o}\). Vậy góc giữa đường thẳng \(BD\) và mặt phẳng \(\left( {DCC'D'} \right)\) bằng \({45^o}\). d) Do \(ABCD.A'B'C'D'\) là hình lập phương, ta suy ra \(DD' \bot \left( {ABCD} \right)\). Điều này dẫn tới \(DD' \bot BD\) và \(DD' \bot CD\). Vậy \(\widehat {BDC}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,DD',C} \right]\). Theo câu c, ta có \(\widehat {BDC} = {45^o}\). Vậy số đo của góc nhị diện \(\left[ {B,DD',C} \right]\) bằng \({45^o}\). e) Gọi \(I\) là giao điểm của \(D'C\) và \(DC'\). Theo câu a, ta có \(C'D \bot \left( {BCD'} \right)\), nên \(DI \bot \left( {BCD'} \right)\). Vậy khoảng cách từ \(D\) đến \(\left( {BCD'} \right)\) là đoạn thẳng \(DI\). Vì \(DCC'D'\) là hình vuông cạnh \(a\), ta suy ra \(C'D = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \). Suy ra \(DI = C'I = \frac{{C'D}}{2} = \frac{{a\sqrt 2 }}{2}\). Vậy khoảng cách từ \(D\) đến \(\left( {BCD'} \right)\) bằng \(\frac{{a\sqrt 2 }}{2}\). g) Do \(ABCD.A'B'C'D'\) là hình lập phương, ta suy ra \(B'C'\parallel BC\). Mà \(BC \subset \left( {BCD} \right)\) nên ta suy ra \(B'C'\parallel \left( {BCD'} \right)\). Vì \(B'C'\parallel \left( {BCD'} \right)\), nên khoảng cách giữa \(B'C'\) và \(\left( {BCD'} \right)\) cũng bằng khoảng cách từ \(C'\) đến \(\left( {BCD'} \right)\). Theo câu a, ta có \(C'D \bot \left( {BCD'} \right)\), điều này cũng có nghĩa \(C'I \bot \left( {BCD'} \right)\), tức khoảng cách từ \(C'\) đến \(\left( {BCD'} \right)\) là đoạn thẳng \(C'I\). Mà theo câu e, vì \(C'I = \frac{{a\sqrt 2 }}{2}\), ta kết luận rằng khoảng cách giữa \(B'C'\) và \(\left( {BCD'} \right)\) bằng \(\frac{{a\sqrt 2 }}{2}\). h) Do \(CC' \bot \left( {BCD} \right)\) nên thể tích tứ diện \(C'BCD\) là \(V = \frac{1}{3}CC'.{S_{BCD}} = \frac{1}{3}CC'.\frac{{BC.CD}}{2} = \frac{{a.a.a}}{6} = \frac{{{a^3}}}{6}\). Tam giác \(BC'D\) có \(BC' = C'D = BD = a\sqrt 2 \) (do chúng đều là đường chéo của các mặt của hình lập phương) nên tam giác đó đều. Diện tích tam giác \(BC'D\) bằng \({S_{BC'D}} = \frac{{B{D^2}\sqrt 3 }}{4} = \frac{{{{\left( {a\sqrt 2 } \right)}^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{2}\). Vì thể tích tứ diện \(C'BCD\) cũng có thể được tính bằng công thức \(V = \frac{1}{3}{d_{C,\left( {BC'D} \right)}}.{S_{BC'D}}\), ta suy ra \({d_{C,\left( {BC'D} \right)}} = \frac{{3.\frac{{{a^3}}}{6}}}{{\frac{{{a^2}\sqrt 3 }}{2}}} = \frac{{a\sqrt 3 }}{3}\). Vậy khoảng cách từ \(C\) đến mặt phẳng \(\left( {BC'D} \right)\) bằng \(\frac{{a\sqrt 3 }}{3}\).
|




















Danh sách bình luận