Trang chủ
SBT Toán 12 - giải SBT Toán 12 - Cánh diều

Giải bài 5 trang 60 sách bài tập toán 12 - Cánh diều

Cho hình lập phương (ABCD.A'B'C'D'). Góc giữa hai vectơ (overrightarrow {AC} ,overrightarrow {DA'} ) bằng: A. ({30^ circ }). B. ({45^ circ }). C. ({120^ circ }). D. ({60^ circ }).

Quảng cáo

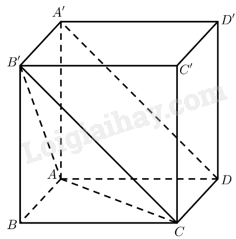
Đề bài

Cho hình lập phương \(ABCD.A'B'C'D'\). Góc giữa hai vectơ \(\overrightarrow {AC} ,\overrightarrow {DA'} \) bằng:

A. \({30^ \circ }\)

B. \({45^ \circ }\)

C. \({120^ \circ }\)

D. \({60^ \circ }\)

Phương pháp giải - Xem chi tiết

‒ Cách xác định góc giữa hai vectơ \(\overrightarrow a ,\overrightarrow b \): \(\left( {\overrightarrow a ,\overrightarrow b } \right) = \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right)\) với \(\overrightarrow {OA}  = \overrightarrow a ,\overrightarrow {OB}  = \overrightarrow b \).

‒ Sử dụng tích vô hướng của hai vectơ: \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\).

Lời giải chi tiết

\(\overrightarrow {AC} .\overrightarrow {DA'}  =  - \overrightarrow {CA} .\overrightarrow {DA'}  =  - \left| {\overrightarrow {CA} } \right|.\left| {\overrightarrow {DA'} } \right|.\cos \left( {\overrightarrow {CA} ,\overrightarrow {DA'} } \right) =  - AC.A'D.\cos \left( {\overrightarrow {CA} ,\overrightarrow {DA'} } \right)\)

Ta có: \(\overrightarrow {CB'}  = \overrightarrow {DA'} \)

\( \Rightarrow \left( {\overrightarrow {CA} ,\overrightarrow {DA'} } \right) = \left( {\overrightarrow {CA} ,\overrightarrow {CB'} } \right) = \widehat {ACB'}\).

Xét tam giác \(ACB'\) có \(AC,AB',B'C\) đều là các đường chéo của các hình vuông là các mặt của hình lập phương.

Do đó \(AC = AB' = B'C\). Vậy tam giác \(ACB'\) đều.

Suy ra \(\left( {\overrightarrow {CA} ,\overrightarrow {DA'} } \right) = \widehat {ACB'} = {60^ \circ }\).

\(\overrightarrow {AC} .\overrightarrow {DA'}  =  - AC.A'D.\cos {60^ \circ } =  - \frac{1}{2}AC.A'D\).

Ta có: \(\cos \left( {\overrightarrow {AC} ,\overrightarrow {DA'} } \right) = \frac{{\overrightarrow {AC} .\overrightarrow {DA'} }}{{\left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {DA'} } \right|}} = \frac{{ - \frac{1}{2}AC.A'D}}{{AC.A'D}} =  - \frac{1}{2}\).

Vậy \(\left( {\overrightarrow {AC} ,\overrightarrow {DA'} } \right) = {120^ \circ }\).

Chọn C.

  • Giải bài 6 trang 60 sách bài tập toán 12 - Cánh diều

    Trong không gian, cho hai vectơ (overrightarrow a ,overrightarrow b ) tạo với nhau một góc ({60^ circ }) và (left| {overrightarrow a } right| = 3cm,left| {overrightarrow b } right| = 4cm). Khi đó (overrightarrow a .overrightarrow b ) bằng: A. 12. B. 6. C. (6sqrt 3 ). D. ‒6.

  • Giải bài 7 trang 61 sách bài tập toán 12 - Cánh diều

    Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Cho hình chóp (S.ABC) có (SA = SB = SC = AB = AC = a) và (BC = asqrt 2 ) (Hình 9). a) Tam giác (ABC) vuông tại (A) và tam giác (SAB) đều. b) (overrightarrow {AB} .overrightarrow {AC} = 0) và (left( {overrightarrow {SA} ,overrightarrow {AB} } right) = {120^ circ }). c) (overrightarrow {SC} .overrightarrow {AB} = frac{{{a^2}}}{2}). d) (cos left( {overrightarrow {SC} ,overrightarrow {AB} } r

  • Giải bài 8 trang 61 sách bài tập toán 12 - Cánh diều

    Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Cho hình chóp tứ giác đều (S.ABCD) có độ dài tất cả các cạnh đều bằng (a) (Hình 10). a) Tứ giác (ABCD) là hình vuông. b) Tam giác (SAC) vuông cân tại (S). c) (left( {overrightarrow {SA} ,overrightarrow {AC} } right) = {45^ circ }). d) (overrightarrow {SA} .overrightarrow {AC} = - {a^2}).

  • Giải bài 9 trang 61 sách bài tập toán 12 - Cánh diều

    Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm \(O\) trên trần nhà lần lượt buộc vào ba điểm \(A,B,C\) trên đèn tròn (Hình 11). Độ dài của ba đoạn dây \(OA,OB,OC\) đều bằng \(L\left( {inch} \right)\). Trọng lượng của chiếc đèn là \(24N\) và bán kính của chiếc đèn là \(18inch\left( {1inch = 2,54cm} \right)\). Gọi \(F\) là độ lớn của các lực căng \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) trên mỗi sợi dâ

  • Giải bài 4 trang 60 sách bài tập toán 12 - Cánh diều

    Cho hình lập phương (ABCD.A'B'C'D'). Góc giữa hai vectơ (overrightarrow {BD} ,overrightarrow {B'C} ) bằng: A. ({30^ circ }). B. ({45^ circ }). C. ({120^ circ }). D. ({60^ circ }).

Quảng cáo
Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
close