Giải bài 5 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo

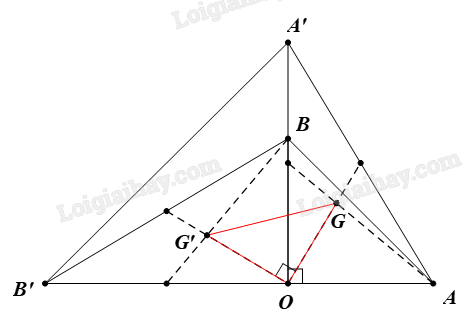
Đề bài

Cho hai tam giác vuông cân OAB và OA’B’ có chung đỉnh O sao cho O nằm trên đoạn AB’ và nằm ngoài đoạn A’B. Gọi G và G’ lần lượt là trọng tâm của \(\Delta \)OAA’ và \(\Delta \)OBB’. Chứng minh rằng \(\Delta \)OGG’ là tam giác vuông cân.

Lời giải chi tiết

Do DOAB là tam giác vuông cân nên OA = OB và \(\widehat {AOB} = 90^\circ \)

Do DOA’B’ là tam giác vuông cân nên OA’ = OB’ và \(\widehat {A'OB'} = 90^\circ \)

Phép quay tâm O, góc quay 90° biến:

⦁ Điểm O thành điểm O;

⦁ Điểm A thành điểm B;

⦁ Điểm A’ thành điểm B’.

Do đó ảnh của \(\Delta \) OAA’ qua phép quay tâm O, góc quay 90° là \(\Delta \) OBB’.

Mà G, G’ lần lượt là trọng tâm của \(\;\Delta OAA',{\rm{ }}\Delta OBB'.\)

Vì vậy ảnh của G qua phép quay tâm O, góc quay 90° là G’.

Suy ra \(OG{\rm{ }} = {\rm{ }}OG'\)  và \(\widehat {GOG'} = \left( {OG,OG'} \right) = 90^\circ \)

DOGG’ có \(OG{\rm{ }} = {\rm{ }}OG'\) và \(\widehat {GOG'} = 90^\circ \)  nên là tam giác vuông cân tại O.

Vậy \(\Delta OGG'\)  vuông cân tại O.