Giải bài 1 trang 28 Chuyên đề học tập Toán 11 Chân trời sáng tạo

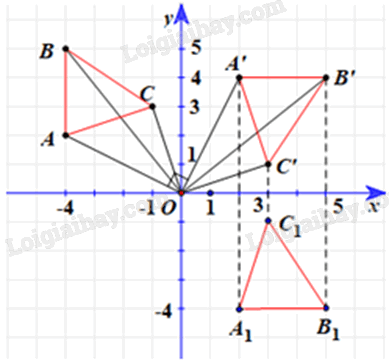
Đề bài

Trong mặt phẳng tọa độ Oxy, cho các điểm \(A\left( {-4;{\rm{ }}2} \right),{\rm{ }}B\left( {-4;{\rm{ }}5} \right)\) và \(C\left( {-1;{\rm{ }}3} \right).\)

a) Chứng minh các điểm \(A'\left( {2;{\rm{ }}4} \right),{\rm{ }}B'\left( {5;{\rm{ }}4} \right){\rm{ }}\) và \(C'\left( {3;{\rm{ }}1} \right)\) theo thứ tự là ảnh của A, B, C qua phép quay tâm O với góc quay –90°.

b) Gọi \(\Delta {A_1}{B_1}{C_1}\) là ảnh của ∆ABC qua phép dời hình có được bằng cách thực hiện phép quay tâm O với góc quay –90° và phép đối xứng qua Ox. Tìm tọa độ các đỉnh của \(\Delta {A_1}{B_1}{C_1}.\)

Lời giải chi tiết

a)

 

Với  ta có \(\overrightarrow {OA}  = \left( { - 4;2} \right),\overrightarrow {OA'}  = \left( {2;4} \right),\overrightarrow {AA'}  = \left( {6;2} \right)\)

Do đó \(OA = OA' = 2\sqrt 5 \) và \(AA' = 2\sqrt {10} \)

Suy ra \(\cos \widehat {AOA'} = \frac{{O{A^2} + OA{'^2} - AA{'^2}}}{{2.OA.OA'}} = \frac{{{{\left( {2\sqrt 5 } \right)}^2} + {{\left( {2\sqrt 5 } \right)}^2} - {{\left( {2\sqrt {10} } \right)}^2}}}{{2.2\sqrt 5 .2\sqrt 5 }} = 0\)

Do đó \(\widehat {AOA'} = 90^\circ \)

Mà khi quay đoạn OA (với tâm O) theo hướng cùng chiều kim đồng hồ một góc 90° thì ta được đoạn OA’. Tức là, phép quay có góc quay lượng giác theo chiều âm một góc 90°.

Vì vậy góc lượng giác \(\left( {OA,{\rm{ }}OA'} \right){\rm{ }} = {\rm{ }}-90^\circ .\)

Vậy A’ là ảnh của A qua phép quay tâm O với góc quay –90°.

Chứng minh tương tự, ta thu được B’, C’ theo thứ tự là ảnh của B, C qua phép quay tâm O với góc quay –90°.

b) Từ câu a, ta có phép quay tâm O, góc quay –90° biến ∆ABC thành ∆A’B’C’.

Ta có: \(\Delta {A_1}{B_1}{C_1}\;\) là ảnh của ∆A’B’C’ qua phép đối xứng trục Ox nên:

• \({A_1}\; = {\rm{ }}{Đ_{Ox}}\left( {A'} \right),\) do đó hai điểm A₁­ và A’(2; 4) có cùng hoành độ và có tung độ đối nhau, suy ra A₁(2; –4).

• \({B_1}\; = {\rm{ }}{{\rm{Đ}}_{Ox}}\left( {B'} \right),\) do đó hai điểm B₁­ và B’(5; 4) có cùng hoành độ và có tung độ đối nhau, suy ra B₁(5; –4).

• \({C_1}\; = {\rm{ }}{Đ_{Ox}}\left( {C'} \right),\)do đó hai điểm C₁­ và C’(3; 1) có cùng hoành độ và có tung độ đối nhau, suy ra C₁(3; –1).

Vậy tọa độ các đỉnh của ∆A₁B₁C₁ thỏa mãn yêu cầu bài toán là \({A_1}\left( {2;{\rm{ }}-4} \right),{\rm{ }}{B_1}\left( {5;{\rm{ }}-4} \right),{\rm{ }}{C_1}\left( {3;{\rm{ }}-1} \right).\)