Giải bài 46 trang 23 sách bài tập toán 11 - Cánh diều

Từ đồ thị hàm số \(y = \sin x\), tìm:

Quảng cáo

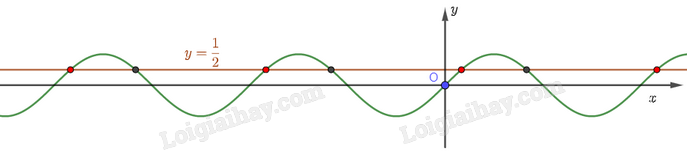
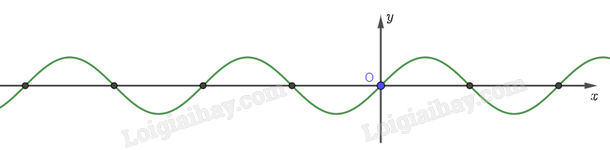
Đề bài

Từ đồ thị hàm số \(y = \sin x\), tìm:

a) Các giá trị của \(x\) để \(\sin x = \frac{1}{2}\).

b) Các khoảng giá trị của \(x\) để hàm số \(y = \sin x\) nhận giá trị dương.

Phương pháp giải - Xem chi tiết

Vẽ đồ thị hàm số \(y = \sin x\).

a) Vẽ đường thẳng \(y = \frac{1}{2}\) và xác định các giao điểm của đường thẳng này với đồ thị hàm số \(y = \sin x\).

b) Từ đồ thị hàm số \(y = \sin x\), xác định những phần đồ thị nằm phía trên trục hoành. Phần đồ thị đó chính là những giá trị dương của hàm số \(y = \sin x\).

Lời giải chi tiết

a) Ta có hình vẽ sau:

Từ hình vẽ, ta thấy giá trị của \(x\) để \(\sin x = \frac{1}{2}\) là hoành độ giao điểm của đường thẳng \(y = \frac{1}{2}\) với đồ thị hàm số \(y = \sin x\). Dựa vào hình vẽ trên, ta thấy \(\sin x = \frac{1}{2}\) khi \(x = \frac{\pi }{6} + k2\pi \) (các giao điểm màu đỏ) và \(x = \frac{{5\pi }}{6} + k2\pi \) (các giao điểm màu đen), với \(k \in \mathbb{Z}\).

b) Ta thấy phần đồ thị nằm phía trên trục hoành là những giá trị dương của hàm số \(y = \sin x\). Dựa vào hình vẽ dưới đây, ta thấy hàm số \(y = \sin x\) nhận giá trị dương khi \(x \in \left( {k2\pi ;\pi + k2\pi } \right)\)