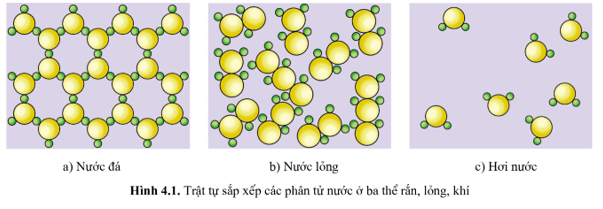
Bài 4. Entropy và biến thiên năng lượng tự do Gibbs - Chuyên đề học tập Hóa 10 Cánh diềuHình 4.1 mô tả trật tự sắp xếp của các phân tử nước ở ba thể: rắn, lỏng và khí. Khi đun nóng chảy tinh thể NaCl, độ mất trật tự của các ion tăng hay giảm? Tại sao? Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
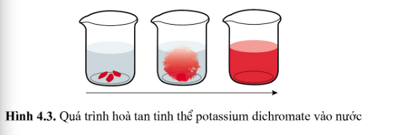
Mở đầu Hình 4.1 mô tả trật tự sắp xếp của các phân tử nước ở ba thể: rắn, lỏng và khí. Em hãy cho biết mức độ “mất trật tự” của hệ tăng hay giảm theo chiều từ nước đá tới hơi nước. Lời giải chi tiết: Mức độ “mất trật tự” của hệ tăng theo chiều từ nước đá tới hơi nước. Câu hỏi 1 Khi đun nóng chảy tinh thể NaCl, độ mất trật tự của các ion tăng hay giảm? Tại sao? Lời giải chi tiết: Khi đun nóng chảy tinh thể NaCl, độ mất trật tự của các ion tăng vì muối ăn đã chuyển từ trạng thái tinh thể sang trạng thái lỏng. Câu hỏi 2 Tính biến thiên entropy chuẩn cho phản ứng đốt cháy 1 mol CH3OH(l) bằng O2(g), thu được CO2(g) và H2O(g) Phương pháp giải: Áp dụng CT: \({\Delta _r}S_{298}^o = \sum {S_{298}^o(sp) - } \sum {S_{298}^o(cd)} \) Lời giải chi tiết: CH3OH(l) + 3/2 O2(g) → CO2(g) + 2H2O(g) \(\begin{array}{l}{\Delta _r}S_{298}^o = S_{298}^o(C{O_2}(g)) + 2.S_{298}^o({H_2}O(g)) - S_{298}^o(C{H_3}OH(l)) - \frac{3}{2}S_{298}^o({O_2}g))\\{\Delta _r}S_{298}^o = 213,8 + 2.188,7 - 126,8 - \frac{3}{2}.205,2 = 156,6J.{K^{ - 1}}\end{array}\) Luyện tập 1 Tính \({\Delta _r}S_{298}^o\) của các phản ứng sau: a) 2Ca(s) + O2(g) → 2CaO(s) b) CH4(g) + 2O2(g) → CO2(g) + 2H2O(g) c) NH3(g) + HCl(g) → NH4Cl(s) Phương pháp giải: Áp dụng CT: \({\Delta _r}S_{298}^o = \sum {S_{298}^o(sp) - } \sum {S_{298}^o(cd)} \) Lời giải chi tiết: a) \({\Delta _r}S_{298}^o = 2.S_{298}^o(CaO(s)) - 2.S_{298}^o(Ca(s)) - S_{298}^o({O_2}(s))\) \({\Delta _r}S_{298}^o\) = 2.38,1 – 2.41,6 – 205,2 = -212,2 JK-1 b) \({\Delta _r}S_{298}^o = S_{298}^o(C{O_2}(g)) + 2.S_{298}^o({H_2}O(g)) - S_{298}^o(C{H_4}(g)) - 2.S_{298}^o({O_2}(g))\) \({\Delta _r}S_{298}^o\) = 213,8 + 2.188,7 – 186,3 – 2.205,2 = -5,5 JK-1 c) \({\Delta _r}S_{298}^o = S_{298}^o(N{H_4}Cl(s)) - S_{298}^o(N{H_3}(g)) - S_{298}^o(HCl(g))\) \({\Delta _r}S_{298}^o\) = 94,6 -192,8 – 186,9 = -285,1 JK-1 Luyện tập 2 Tại sao \({\Delta _r}S_{298}^o\) của quá trình (1) lại dương? Lời giải chi tiết: Độ “mất trật tự” của phân tử hơi nước là lớn hơn các phân tử nước lỏng ⇒ Entropy của hơn nước (H2O(g)) lớn hơn entropy của nước lỏng (H2O(l)) Luyện tập 3 Tính \({\Delta _r}G_{298}^o\) của các phản ứng sau và cho biết ở điều kiện chuẩn các phản ứng có tự xảy ra hay không. a) H2(g) + Cl2(g) → 2HCl(g) \({\Delta _r}H_{298}^o\) = -184,6 kJ b) CH4(g) + 2O2(g) → CO2(g) + 2H2O(l) \({\Delta _r}H_{298}^o\) = -890,3 kJ c) 2Na(s) + O2(g) → Na2O2(s) \({\Delta _r}H_{298}^o\) = -510,9 kJ Phương pháp giải: Tính entropy theo CT \({\Delta _r}S_{298}^o = \sum {S_{298}^o(sp) - } \sum {S_{298}^o(cd)} \) Tính Năng lượng tự do Gibbs theo CT: \({\Delta _r}G_T^o = {\Delta _r}H_T^o - T.{\Delta _r}S_T^o\) Lời giải chi tiết: a)\({\Delta _r}S_{298}^o = 2.S_{298}^o(HCl(g)) - S_{298}^o({H_2}(g)) - S_{298}^o(C{l_2}(g))\) \({\Delta _r}S_{298}^o\) = 2.186,9 – 130,7 – 223,1 = 20 JK-1 \({\Delta _r}G_T^o = {\Delta _r}H_T^o - T.{\Delta _r}S_T^o\) Ở điều kiện chuẩn T = 298K Ta có: \({\Delta _r}G_{298}^o = {\Delta _r}H_{298}^o - 298.{\Delta _r}S_{298}^o\) = -184,6.103 – 298.20 = -190560 J < 0 Vậy ở điều kiện chuẩn phản ứng này tự xảy ra b) \({\Delta _r}S_{298}^o = S_{298}^o(C{O_2}(g)) + 2.S_{298}^o({H_2}O(g)) - S_{298}^o(C{H_4}(g)) - 2.S_{298}^o({O_2}(g))\) \({\Delta _r}S_{298}^o\) = 213,8 + 2.188,7 – 186,3 – 2.205,2 = -5,5 JK-1 Ở điều kiện chuẩn T = 298K Ta có: \({\Delta _r}G_{298}^o = {\Delta _r}H_{298}^o - 298.{\Delta _r}S_{298}^o\) = -890,3.103 – 293.(-5,5) = -888661 J < 0 Vậy ở điều kiện chuẩn phản ứng này tự xảy ra c) \({\Delta _r}S_{298}^o = S_{298}^o(N{a_2}{O_2}(s)) - 2.S_{298}^o(Na(s)) - .S_{298}^o({O_2}(g))\) \({\Delta _r}S_{298}^o\) = 95,0 – 2.51,3 – 205,2 = 212,8 JK-1 Ở điều kiện chuẩn T = 298K Ta có: \({\Delta _r}G_{298}^o = {\Delta _r}H_{298}^o - 298.{\Delta _r}S_{298}^o\) = -510,9.103 – 298.(-212,8) = -447485 J < 0 Vậy ở điều kiện chuẩn phản ứng này tự xảy ra. Vận dụng 1 Từ giá trị \({\Delta _r}G_T^o\) của phản ứng (2) ở nhiệt độ 298 K và 273 K, hãy cho biết ở nhiệt độ thấp hơn hay cao hơn thì phản ứng diễn ra thuận lợi hơn? Lời giải chi tiết: Trong phản ứng (2), \({\Delta _r}G_{273}^o\) = -79050 J có giá trị âm hơn \({\Delta _r}G_{298}^o\) = -75300 J vì thế ở nhiệt độ thấp hơn thì phản ứng diễn ra thuận lợi hơn. Vận dụng 2 Phản ứng (3) trong thực tế còn gọi là phản ứng gì? Lời giải chi tiết: Phản ứng (3) trong thực tế còn gọi là phản ứng nung vôi Vận dụng 3 Mặc dù phản ứng (3) có thể xảy ra ở nhiệt độ 848oC, nhưng trong thực tế người ta thường nung nóng CaCO3 tới nhiệt độ 1 000oC. Giải thích vì sao? Lời giải chi tiết: Mặc dù phản ứng (3) có thể xảy ra ở nhiệt độ 848oC, nhưng trong thực tế người ta thường nung nóng CaCO3 tới nhiệt độ 1 000oC vì ở nhiệt độ khoảng 1 000oC thì phản ứng xảy ra mãnh liệt và ào ạt làm tăng năng suất sản xuất vôi sống từ đá vôi. Bài 1 Thả một vài tinh thể patassium dichromate K2Cr2O7 màu cam đỏ vào nước (Hình 4.3). Entropy của quá trình hòa tan này tăng hay giảm? Giải thích. Lời giải chi tiết: Thả một vài tinh thể patassium dichromate K2Cr2O7 màu cam đỏ vào nước, tinh thể patassium dichromate K2Cr2O7 tan trong nước ⇒ Độ mất trật tự của các ion trong tinh thể tăng ⇒ Entropy của quá trình hòa tan này tăng. Bài 2 Hãy đánh giá khả năng tự xảy ra của phản ứng sau ở nhiệt độ chuẩn: 2Al(s) + 3H2O(l) → Al2O3(s) + 3H2(g) Biết rằng: \({\Delta _r}H_{298}^o\) = -818,3 kJ, \({\Delta _r}H_{298}^o\) được tính theo số liệu cho trong Phụ lục 1. Từ kết quả này hãy đưa ra một số lí do giải thích cho việc vì sao các đồ vật bằng nhôm được sử dụng rất phổ biến. Phương pháp giải: Tính entropy theo CT \({\Delta _r}S_{298}^o = \sum {S_{298}^o(sp) - } \sum {S_{298}^o(cd)} \) Tính Năng lượng tự do Gibbs theo CT: \({\Delta _r}G_T^o = {\Delta _r}H_T^o - T.{\Delta _r}S_T^o\) \({\Delta _r}{G_T} > 0\) -> phản ứng không tự xảy ra \({\Delta _r}{G_T} < 0\) -> phản ứng tự xảy ra
Lời giải chi tiết: \({\Delta _r}S_{298}^o = S_{298}^o(A{l_2}{O_3}(s)) + 3.S_{298}^o({H_2}(g)) - 2.S_{298}^o(Al(s)) - 3.S_{298}^o({H_2}O(l))\) \({\Delta _r}S_{298}^o\) = 50,9 + 3.130,7 – 2.28,3 – 3.70,0 = 176,4 JK-1 Ở điều kiện chuẩn T = 298K Ta có: \({\Delta _r}G_{298}^o = {\Delta _r}H_{298}^o - 298.{\Delta _r}S_{298}^o\) = -818,3.103 – 298.176,4 = -870867,2 J < 0 \({\Delta _r}G_{273}^o\) rất âm ở điều kiện chuẩn vì thế phản ứng này tự xảy ra. Các đồ vật bằng nhôm được sử dụng rất phổ biến vì Al phản ứng dễ dàng với H2O ở điều kiện chuẩn để tạo thành lớp màng nhôm oxide Al2O3 bền vững. Lớp màng này bảo vệ cho nhôm kim loại chống lại các tác động ăn mòn của môi trường. Bài 3 Hãy xác định nhiệt độ sôi của CHCl3(l) ở 1 bar và so sánh với giá trị đo được từ thực nghiệm (61,2oC). Giả thiết biến thiên enthalpy và entropy của quá trình không thay đổi theo nhiệt độ. Biết rằng
Phương pháp giải: Tính entropy theo CT \({\Delta _r}S_{298}^o = \sum {S_{298}^o(sp) - } \sum {S_{298}^o(cd)} \) Tính Năng lượng tự do Gibbs theo CT: \({\Delta _r}G_T^o = {\Delta _r}H_T^o - T.{\Delta _r}S_T^o\) Lời giải chi tiết: CHCl3(l) → CHCl3(g) \(\begin{array}{l}\Delta H_{298}^o = {\Delta _f}H_{298}^o(CHC{l_3}(g)) - {\Delta _f}H_{298}^o(CHC{l_3}(l))\\\Delta H_{298}^o = - 102,7 - ( - 134,1) = 31,4kJ\\\Delta S_{298}^o = S_{298}^o(CHC{l_3}(g)) - S_{298}^o(CHC{l_3}(l))\\\Delta S_{298}^o = 295,7 - 201,7 = 94J.{K^{ - 1}}\end{array}\) Ở điều kiện chuẩn T = 298K, 1 bar Ta có: \(\Delta G_{298}^o = \Delta H_{298}^o - 298.\Delta S_{298}^o\) = 31,4.103 – 298.94 = 3388J Thực nghiệm T = 61,2 + 273 = 334,2K \(\Delta G_{334,2}^o = \Delta H_{298}^o - 334,2.\Delta S_{298}^o\) = 31,4.103 - 334,2.94 = -14,8 J Thực nghiệm đo được giá trị \({\Delta _r}G_{334,2}^o\) âm hơn giá trị \({\Delta _r}G_{298}^o\) Bài 4 Cho phản ứng: ZnCO3(s) → ZnO(s) + CO2(g) Ở điều kiện chuẩn, phản ứng có tự xảy ra tại các nhiệt độ sau hay không? a) 25oC b) 500oC Biết rằng: \({\Delta _r}H_{298}^o\) = 710 kJ, \({\Delta _r}S_{298}^o\) = 174,8 J.K-1. Giả sử biến thiên enthalpy và biến thiên entropy của phản ứng không phụ thuộc vào nhiệt độ. Phương pháp giải: Tính Năng lượng tự do Gibbs theo CT: \({\Delta _r}G_T^o = {\Delta _r}H_T^o - T.{\Delta _r}S_T^o\) \({\Delta _r}{G_T} > 0\) -> phản ứng không tự xảy ra \({\Delta _r}{G_T} < 0\) -> phản ứng tự xảy ra Lời giải chi tiết: a) Ở 25oC = 298 K \({\Delta _r}G_{298}^o = {\Delta _r}H_{298}^o - 298.{\Delta _r}S_{298}^o\) = 710.103 – 298.174,8 = 657909,6 J > 0 => Phản ứng không tự xảy ra ở 25oC b) Ở 500oC = 500 + 273 = 773 K \({\Delta _r}G_{773}^o = {\Delta _r}H_{298}^o - 773.{\Delta _r}S_{298}^o\) = 710.103 – 773.174,8 = 574879,6 > 0 => Phản ứng không tự xảy ra ở 500oC Bài 5 Hãy xác định nhiệt độ thấp nhất để phản ứng nhiệt phân NaHCO3 dưới đây diễn ra: 2NaHCO3(s) → Na2CO3(s) + H2O(l) + CO2(g) Biết rằng: \({\Delta _r}H_{298}^o\) = 9,16 kJ, \({\Delta _r}S_{298}^o\) được tính theo số liệu cho trong Phụ lục 1. Giả sử biến thiên enthalpy và biến thiên entropy của phản ứng không phụ thuộc vào nhiệt độ. Phương pháp giải: Tính entropy theo CT \({\Delta _r}S_{298}^o = \sum {S_{298}^o(sp) - } \sum {S_{298}^o(cd)} \) Tính Năng lượng tự do Gibbs theo CT: \({\Delta _r}G_T^o = {\Delta _r}H_T^o - T.{\Delta _r}S_T^o\) \({\Delta _r}{G_T} > 0\) -> phản ứng không tự xảy ra \({\Delta _r}{G_T} < 0\) -> phản ứng tự xảy ra Lời giải chi tiết: \({\Delta _r}S_{298}^o = S_{298}^o(N{a_2}C{O_3}(s)) + S_{298}^o({H_2}O(l)) + S_{298}^o(C{O_2}(g)) - 2.S_{298}^o(NaHC{O_3}(s))\) \({\Delta _r}S_{298}^o\) = 135,0 + 70,0 + 213,8 – 2.101,7 = 215,4 J.K-1 Để phản ứng diễn ra cần có \({\Delta _r}G_T^o = {\Delta _r}H_{298}^o - T.{\Delta _r}S_{298}^o\) < 0 => 9,16.103 – T.215,4 < 0 => T > 42,53K hay T > -230,47oC Bài 6 Ở điều kiện thường (coi là 25oC, 1 bar), có tự xảy ra quá trình sắt bị biến đổi thành Fe2O3(s) (có trong thành phần gỉ sắt) được không? Phương pháp giải: Tính entropy theo CT \({\Delta _r}S_{298}^o = \sum {S_{298}^o(sp) - } \sum {S_{298}^o(cd)} \) Tính Năng lượng tự do Gibbs theo CT: \({\Delta _r}G_T^o = {\Delta _r}H_T^o - T.{\Delta _r}S_T^o\) \({\Delta _r}{G_T} > 0\) -> phản ứng không tự xảy ra \({\Delta _r}{G_T} < 0\) -> phản ứng tự xảy ra Lời giải chi tiết: 4Fe(s) + 3O2(g) → 2Fe2O3(s) \(\begin{array}{l}{\Delta _r}H_{298}^o = 2.{\Delta _f}H_{298}^o(F{e_2}{O_3}(s)) - 3.{\Delta _f}H_{298}^o({O_2}(g)) - 4.{\Delta _f}H_{298}^o(Fe(s))\\{\Delta _r}H_{298}^o = 2.( - 824,2) - 3.0 - 4.0 = - 1648,4kJ\\{\Delta _r}S_{298}^o = 2.S_{298}^o(F{e_2}{O_3}(s)) - 3.S_{298}^o({O_2}(g)) - 4.S_{298}^o(Fe(s))\\{\Delta _r}S_{298}^o = 2.87,4 - 3.205,2 - 4.27,3 = - 550J.{K^{ - 1}}\end{array}\) \({\Delta _r}G_{298}^o = {\Delta _r}H_{298}^o - T.{\Delta _r}S_{298}^o\) = -1648,4.103 – 298.(-550) = -1484500 J < 0 => Ở điều kiện thường có thể tự xảy ra quá trình sắt bị biến đổi thành Fe2O3(s) Bài 7 Để dự đoán khả năng tự xảy ra phản ứng cần sử dụng ΔrHo và ΔrGo. Giải thích Lời giải chi tiết: Biến thiên năng lượng tự do Gibbs, ΔrGo là tiêu chuẩn để đánh giá khả năng tự diễn biến của quá trình hoặc phản ứng hóa học ở nhiệt độ T và các yếu tố khác ở điều kiện chuẩn. Tại một nhiệt độ T: ΔrGo = ΔrHo - T∆So
|




















Danh sách bình luận