SBT Toán 11 - giải SBT Toán 11 - Cánh diều

Giải bài 35 trang 109 sách bài tập toán 11 - Cánh diều

Cho hai hình bình hành \(ABCD\) và \(ABEF\) không cùng nằm trong một mặt phẳng

Quảng cáo

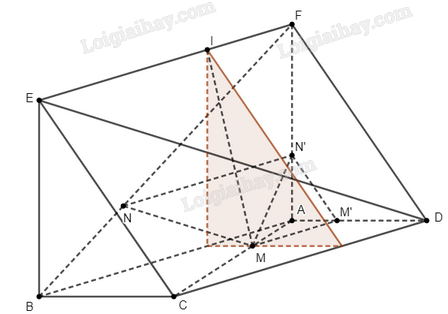
Đề bài

Cho hai hình bình hành \(ABCD\) và \(ABEF\) không cùng nằm trong một mặt phẳng. Trên các đường chéo \(AC\), \(BF\) lần lượt lấy các điểm \(M\), \(N\) sao cho \(\frac{{AM}}{{AC}} = \frac{{BN}}{{BF}}\). Qua \(M\) vẽ đường thẳng song song với \(AB\) cắt \(AD\) tại \(M'\), qua \(N\) vẽ đường thẳng song song với \(AB\) cắt \(AF\) tại \(N'\).

a) Chứng minh rằng \(\left( {MNN'} \right)\parallel \left( {CDE} \right)\).

b) Gọi \(\left( P \right)\) là mặt phẳng đi qua \(M\) và song song với mặt phẳng \(\left( {AFD} \right)\). Mặt phẳng \(\left( P \right)\) cắt đường thẳng \(EF\) tại \(I\). Tính \(\frac{{FI}}{{FE}}\), biết \(\frac{{AM}}{{AC}} = \frac{1}{3}\).

Phương pháp giải - Xem chi tiết

a) Chỉ ra rằng \(MM'\parallel NN'\), từ đó suy ra 4 điểm \(M\), \(M'\), \(N\), \(N'\) đồng phẳng. Tương tự 4 điểm \(C\), \(D\), \(E\), \(F\) cũng đồng phẳng.

Chứng minh rằng \(NN'\parallel CD\) (do cùng song song với \(AB\)) để suy ra \(NN'\parallel \left( {CDE} \right)\). Tiếp theo, chỉ ra rằng \(M'N'\parallel FD\) để suy ra \(M'N'\parallel \left( {CDE} \right)\), rồi suy ra điều phải chứng minh.

b) Sử dụng định lí Thales: Đường thẳng \(AC\) cắt ba mặt phẳng \(\left( {ADF} \right)\), \(\left( P \right)\), \(\left( {BCE} \right)\) lần lượt tại \(A\), \(M\), \(C\). Đường thẳng \(FE\) cắt ba mặt phẳng \(\left( {ADF} \right)\), \(\left( P \right)\), \(\left( {BCE} \right)\) lần lượt tại \(F\), \(I\), \(E\). Suy ra \(\frac{{AM}}{{FI}} = \frac{{MC}}{{IE}} = \frac{{CA}}{{EF}}\), từ đó tính được tỉ số \(\frac{{FI}}{{FE}}\).

Lời giải chi tiết

a) Ta có \(MM'\parallel AB\), \(NN'\parallel AB \Rightarrow MM'\parallel NN'\). Suy ra 4 điểm \(M\), \(M'\), \(N\), \(N'\) đồng phẳng. Chứng minh tương tự ta cũng có 4 điểm \(C\), \(D\), \(E\), \(F\) đồng phẳng.

Mặt khác, ta có \(MM'\parallel AB\), \(AB\parallel CD\) nên \(MM'\parallel CD\).

Do \(CD \subset \left( {CDFE} \right)\) nên ta kết luận rằng \(MM'\parallel \left( {CDFE} \right)\).

Hơn nữa, do \(MM'\parallel AB\), nên theo định lí Thales ta có \(\frac{{AM}}{{AC}} = \frac{{AM'}}{{AD}}\).

Chứng minh tương tự ta cũng có \(\frac{{BN}}{{BF}} = \frac{{AN'}}{{AF}}\).

Theo đề bài, vì \(\frac{{AM}}{{AC}} = \frac{{BN}}{{BF}}\), ta suy ra \(\frac{{AM'}}{{AD}} = \frac{{AN'}}{{AF}}\), tức là \(M'N'\parallel FD\).

Do \(FD \subset \left( {CDFE} \right)\) nên ta kết luận rằng \(M'N'\parallel \left( {CDFE} \right)\).

Vì \(MM'\parallel \left( {CDFE} \right)\), \(M'N'\parallel \left( {CDFE} \right)\), \(MM' \cap M'N' = \left\{ {M'} \right\}\), nên ta có \(\left( {MNN'M'} \right)\parallel \left( {CDFE} \right)\), tức là \(\left( {MNN'} \right)\parallel \left( {CDE} \right)\). Bài toán được chứng minh.

b) Ta có \(AD\parallel BE\), \(BC \subset \left( {BCE} \right)\) nên \(AD\parallel \left( {BCE} \right)\). Tương tự ta cũng có \(DF\parallel \left( {BCE} \right)\). Vậy \(\left( {ADF} \right)\parallel \left( {BCE} \right)\)

Theo đề bài, vì \(\left( P \right)\parallel \left( {AFD} \right)\) và \(M \in \left( P \right)\), nên ba mặt phẳng \(\left( {ADF} \right)\), \(\left( P \right)\) và \(\left( {BCE} \right)\) đôi một phân biệt, và chúng cũng đôi một song song.

Đường thẳng \(AC\) cắt ba mặt phẳng \(\left( {ADF} \right)\), \(\left( P \right)\), \(\left( {BCE} \right)\) lần lượt tại \(A\), \(M\), \(C\). Đường thẳng \(FE\) cắt ba mặt phẳng \(\left( {ADF} \right)\), \(\left( P \right)\), \(\left( {BCE} \right)\) lần lượt tại \(F\), \(I\), \(E\). Áp dụng định lí Thales, ta suy ra \(\frac{{AM}}{{FI}} = \frac{{MC}}{{IE}} = \frac{{CA}}{{EF}} \Rightarrow \frac{{AM}}{{FI}} = \frac{{CA}}{{EF}} \Rightarrow \frac{{AM}}{{AC}} = \frac{{FI}}{{FE}}\).

Mà \(\frac{{AM}}{{AC}} = \frac{1}{3}\), ta kết luận \(\frac{{FI}}{{FE}} = \frac{1}{3}\).