Bài 33 trang 79 Vở bài tập toán 9 tập 1

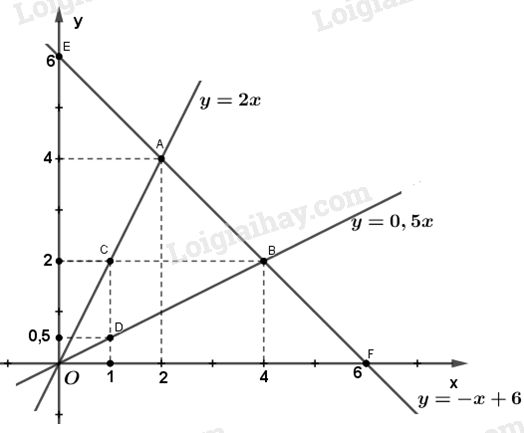
Đề bài

a) Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ:

y = 2x              (1)

y = 0,5x           (2)

y = -x + 6        (3)

b) Gọi các giao điểm của đường thẳng có phương trình (3) với hai đường thẳng có phương trình (1) và (2) theo thứ tự là A và B. Tìm tọa độ của hai điểm A và B.

c) Tính các góc của tam giác OAB.

Lời giải chi tiết

a) Vẽ đồ thị:

- Đường thẳng \(y = 2x\left( 1 \right)\) đi qua gốc tọa độ O và điểm \(C\left( {1;2} \right)\)

- Đường thẳng \(y = 0,5x{\rm{  }}\left( 2 \right)\)  đi qua gốc tọa độ O và điểm \(D\left( {1;0,5} \right)\)

- Đường thẳng \(y =  - x + 6{\rm{ (3)}}\) đi qua hai điểm : \(E\left( {0;6} \right)\) và điểm \(F\left( {6;0} \right)\)

 

b) Tìm tọa độ của điểm A :

\( - x + 6 = 2x \Leftrightarrow x = 2\)

Thay \(x = 2\) vào phương trình \(y = 2x\) ta có \(y = 2.2 = 4\)

Vậy ta có điểm \(A\left( {2;4} \right)\).

- Tìm tọa độ của điểm B :

\( - x + 6 = 0,5x \Leftrightarrow x = 4\)

Thay \(x = 4\) vào phương trình \(y = 0,5x\) ta có :

\(y = 0,5.4 = 2\)

Vậy ta có điểm \(B\left( {4;2} \right)\) 

c) Chứng minh: \(OA = OB\)

\(OA = \sqrt {{4^2} + {2^2}}  = \sqrt {20} \) ; \(OB = \sqrt {{4^2} + {2^2}}  = \sqrt {20} \)

Vậy \(OA = OB \Rightarrow \Delta OAB\) là tam giác cân \( \Rightarrow \widehat {OAB} = \widehat {OBA}\)

Tính góc \(\widehat {AOF}\) : \(\tan \widehat {AOF} = 2 \Rightarrow \widehat {AOF} \approx {63^o}26'\)

Tính góc \(\widehat {BOF}\) : \(\tan \widehat {BOF} = 0,5 \Rightarrow \widehat {BOF} \approx {26^o}34'\)

Vậy \(\widehat {AOB} = \widehat {AOF} - \widehat {BOF}\)\( \approx {63^o}26' - {26^o}34' = {36^o}52'\)

\(\widehat {OAB} = \widehat {OBA}\)\( \approx \dfrac{{{{180}^o} - {{36}^o}52'}}{2} = {71^o}34'.\)

Loigiaihay.com