Giải bài 3.10 trang 66 Chuyên đề học tập Toán 11 Kết nối tri thức

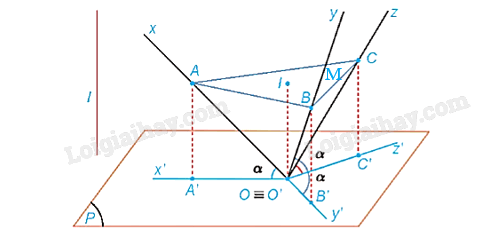
Đề bài

Trong HĐ7, bằng cách xét tam giác vuông OIA và tính tỉ số \(\frac{{IA}}{{OA}}\) , chứng minh rằng trong phép chiếu trục đo vuông góc đều thì \(p = q = r = \frac{{\sqrt 6 }}{3}\).

Lời giải chi tiết

Gọi M là trung điểm của BC.

Ta có: O.ABC là hình chóp tam giác đều nên OA = OB = OC. 

Vì I là tâm tam giác đều ABC nên . (1)

Tam giác OBC vuông cân tại O nên OM vừa là đường cao, vừa là đường phân giác, vừa là đường trung tuyến.

Suy ra \(OM = \frac{1}{2}BC\)  hay 2OM = BC.

Tam giác vuông cân OBC có \(2O{B^2}\; = {\rm{ }}B{C^2}.\)

Do đó: \(2O{B^2}\; = {\rm{ }}4O{M^2}\). Suy ra \(O{M^2}\; = \frac{1}{2}O{A^2}.{\rm{ }}\left( 2 \right)\)

Tam giác OIM vuông tại I có: \(O{I^2}\; + {\rm{ }}I{M^2}\; = {\rm{ }}O{M^2}.{\rm{ }}\left( 3 \right)\)

Mà \(O{I^2}\; = {\rm{ }}O{A^2}\;-{\rm{ }}I{A^2}\) (tam giác OIA vuông tại I) (4)

Thay (1), (2), (4) vào (3) ta được: \(O{A^2} - I{A^2} + \frac{1}{4}I{A^2} = \frac{1}{2}O{A^2}\)

Suy ra \(\frac{{I{A^2}}}{{O{A^2}}} = \frac{2}{3}\) nên \(\frac{{IA}}{{OA}} = \frac{{\sqrt 6 }}{3}\).

Mà IA = O'A' (do AIO'A' là hình bình hành).

Do đó, \(p = q = r = \frac{{O'A'}}{{OA}} = \frac{{\sqrt 6 }}{3}\).