Giải bài 30 trang 95 sách bài tập Toán 6 – Cánh Diều Tập 2a) Vẽ đoạn thẳng AB có độ dài 8 cm và trung điểm C của đoạn thẳng đó. b) Vẽ các điểm P, Q lần lượt là trung điểm của các đoạn thẳng AC và CB c) Tính độ dài các đoạn thẳng AP, QB và PQ. Quảng cáo
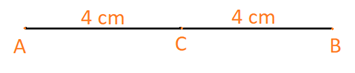
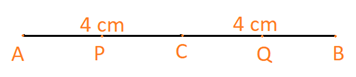
Đề bài a) Vẽ đoạn thẳng AB có độ dài 8 cm và trung điểm C của đoạn thẳng đó. b) Vẽ các điểm P, Q lần lượt là trung điểm của các đoạn thẳng AC và CB c) Tính độ dài các đoạn thẳng AP, QB và PQ. Phương pháp giải - Xem chi tiết Trung điểm O của đoạn thẳng AB là điểm nằm giữa A và B sao cho \(OA = OB\) Nếu O là trung điểm của đoạn thẳng AB thì \(OA = OB = \frac{{AB}}{2}\) Lời giải chi tiết a) Đoạn thẳng AB có độ dài 8 cm và C là trung điểm của đoạn thẳng đó.
Vì C là trung điểm AB nên \(CA = CB = \frac{{AB}}{2} = \frac{8}{2}= 4\,cm\) b) P, Q lần lượt là trung điểm của các đoạn thẳng AC và CB c) Ta có: P là trung điểm AC nên \(PA = PC = \frac{{AC}}{2} = \frac{4}{2}= 2\,cm\) Q là trung điểm BC nên \(QB = QC = \frac{{BC}}{2} = \frac{4}{2}=2\,cm\) Mà: \(PQ = PC + CQ\)(vì C nằm giữa P và Q) \( \Rightarrow PQ = 2 + 2 = 4\,(cm)\) Vậy \(AP = 2\,cm;\;QB = 2\,cm;\;PQ = 4\,cm\)  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K13 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
