Giải bài 2.5 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thứcMột hãng bán gà rán nghiên cứu thấy rằng để làm ra món gà rán có chất lượng tốt nhất thì thức ăn cho gà cần được bổ sung thêm 4 loại vitamin V1, V2, V3 và V4. Tổng lượng vitamin tối thiểu phải bổ sung cho mỗi 100 gam thức ăn cho gà là: V1 cần 50 đơn vị, V2 cần 100 đơn vị, V3 cần 60 đơn vị và V4 cần 180 đơn vị. Có hai loại thức ăn S1 và S2 cung cấp 4 loại vitamin này. Loại S1 có giá 720 đồng một gam và mỗi gam S1 có chứa 5 đơn vị V1, 25 đơn vị V2, 10 đơn vị V3 và 35 đơn vị V4. Loại S2 có giá 960 Quảng cáo
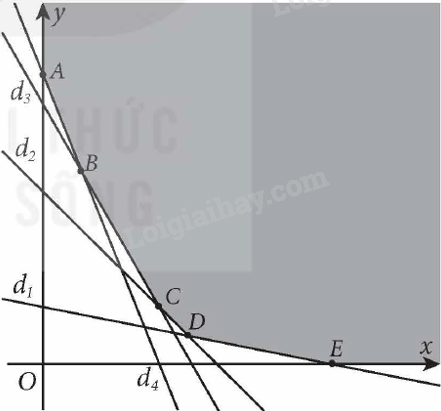
Đề bài Một hãng bán gà rán nghiên cứu thấy rằng để làm ra món gà rán có chất lượng tốt nhất thì thức ăn cho gà cần được bổ sung thêm 4 loại vitamin V1, V2, V3 và V4. Tổng lượng vitamin tối thiểu phải bổ sung cho mỗi 100 gam thức ăn cho gà là: V1 cần 50 đơn vị, V2 cần 100 đơn vị, V3 cần 60 đơn vị và V4 cần 180 đơn vị. Có hai loại thức ăn S1 và S2 cung cấp 4 loại vitamin này. Loại S1 có giá 720 đồng một gam và mỗi gam S1 có chứa 5 đơn vị V1, 25 đơn vị V2, 10 đơn vị V3 và 35 đơn vị V4. Loại S2 có giá 960 đồng một gam và mỗi gam S2 có chứa 25 đơn vị V1, 10 đơn vị V2, 10 đơn vị V3 và 20 đơn vị V4. Hỏi cần phải thêm vào 100 gam thức ăn cho gà mỗi loại S1 và S2 bao nhiêu gam để chi phí là thấp nhất mà vẫn đảm bảo dinh dưỡng cho gà. Phương pháp giải - Xem chi tiết Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Vì miền chấp nhận được không là miền đa giác và có x ≥ 0, y ≥ 0 nên F(x; y) có giá trị nhỏ nhất trên S và đạt được tại một trong các điểm cực biên của miền chấp nhận được. Lời giải chi tiết Gọi x, y lần lượt là số gam thức ăn loại S1 và S2 cần thêm vào 100 gam thức ăn cho gà. Chi phí mua thức ăn là: F(x; y) = 720x + 960y (đồng). Ta có hệ bất phương trình sau: \(\left\{ \begin{array}{l}x \ge 0,y \ge 0\\5x + 25y \ge 50\\25x + 10y \ge 100\\10x + 10y \ge 60\\35x + 20y \ge 180\end{array} \right.\) Miền nghiệm của hệ bất phương trình này là miền tô màu, không bị chặn như hình vẽ dưới đây:
Các điểm cực biên là: A(0; 10),\(B\left( {\frac{4}{3};\frac{{20}}{3}} \right)\), C(4; 2), D(5; 1), E(10; 0). F(0; 10) = 720.0 + 960.10 = 9 600; \(F\left( {\frac{4}{3};\frac{{20}}{3}} \right) = 720 \cdot \frac{4}{3} + \;960 \cdot \frac{{20}}{3} = 7360;\) F(4; 2) = 720.4 + 960.2 = 4 800; F(5; 1) = 720.5 + 960.1 = 4 560; F(10; 0) = 720.10 + 960.0 = 7 200. Do đó giá trị nhỏ nhất của F(x; y) bằng 4 560 tại điểm cực biên D(5; 1). Vậy cần phải thêm vào 100 gam thức ăn cho gà là 5 g loại S1 và 1 g loại S2 để chi phí là thấp nhất mà vẫn đảm bảo dinh dưỡng cho gà.
|




















Danh sách bình luận