Giải bài 2.4 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thứcChế độ ăn của một người yêu cầu mỗi ngày tối thiểu 400 đơn vị vitamin, 500 đơn vị khoáng chất và 1 400 đơn vị calo. Có hai loại thức ăn F1 và F2 mỗi đơn vị F1 giá 1 200 đồng và mỗi đơn vị F2 giá 720 đồng. Mỗi đơn vị thức ăn F1 chứa 2 đơn vị vitamin, 1 đơn vị khoáng chất và 4 đơn vị calo. Mỗi đơn vị thức ăn F2 chứa 1 đơn vị vitamin, 2 đơn vị khoáng chất và 4 đơn vị calo. Tìm chế độ hỗn hợp F1 và F2 sao cho chi phí là ít nhất mà vẫn đảm bảo các yêu cầu về dinh dưỡng. Tổng hợp đề thi giữa kì 2 lớp 12 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh Quảng cáo
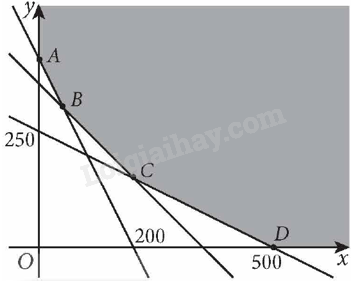
Đề bài Chế độ ăn của một người yêu cầu mỗi ngày tối thiểu 400 đơn vị vitamin, 500 đơn vị khoáng chất và 1 400 đơn vị calo. Có hai loại thức ăn F1 và F2 mỗi đơn vị F1 giá 1 200 đồng và mỗi đơn vị F2 giá 720 đồng. Mỗi đơn vị thức ăn F1 chứa 2 đơn vị vitamin, 1 đơn vị khoáng chất và 4 đơn vị calo. Mỗi đơn vị thức ăn F2 chứa 1 đơn vị vitamin, 2 đơn vị khoáng chất và 4 đơn vị calo. Tìm chế độ hỗn hợp F1 và F2 sao cho chi phí là ít nhất mà vẫn đảm bảo các yêu cầu về dinh dưỡng. Phương pháp giải - Xem chi tiết Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Vì miền chấp nhận được không là miền đa giác và có x ≥ 0, y ≥ 0 nên F(x; y) có giá trị nhỏ nhất trên S và đạt được tại một trong các điểm cực biên của miền chấp nhận được. Lời giải chi tiết Gọi x và y lần lượt là chế ăn hỗn hợp F1 và F2. Chi phí cho thức ăn là: 1 200x + 720y (đồng). Ta có hệ bất phương trình sau: \(\left\{ \begin{array}{l}x \ge 0;y \ge 0\\2{\rm{x}} + y \ge 400\\x + 2y \ge 500\\4{\rm{x}} + 4y \ge 1{\rm{ }}400\end{array} \right.\) Miền nghiệm của hệ bất phương trình này là miền tô màu, không bị chặn như hình vẽ dưới đây:
Các điểm cực biên là: A(0; 400), B(50; 300), C(200; 150), D(500; 0). Ta có: F(0; 400) = 1 200.0 + 720.400 = 288 000; F(50; 300) = 1 200.50 + 720.300 = 276 000; F(200; 150) = 1 200.200 + 720.150 = 348 000; F(500; 0) = 1 200.500 + 720.0 = 600 000. Do đó giá trị nhỏ nhất của F(x; y) bằng 276 000 tại điểm cực biên B(50; 300). Vậy để chi phí là ít nhất mà vẫn đảm bảo các yêu cầu về dinh dưỡng thì cần 50 chế ăn loại F1 và 300 chế ăn loại F2.
|




















Danh sách bình luận