Bài 24 trang 157 Vở bài tập toán 8 tập 1

Đề bài

Tính diện tích hình thoi có cạnh dài \(6\,cm\) và một trong các góc của nó có số đo là \(60^{\circ}\)

Lời giải chi tiết

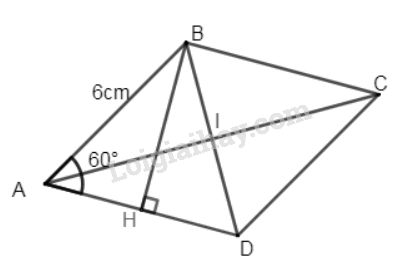
Xét hình thoi \(ABCD\) có \(AB = 6\,cm\), \(\widehat{A}\) = \(60^{\circ}\) 

\(∆ABD\) là tam giác đều vì \(AB=AD\) và  \(\widehat{A}\) = \(60^{\circ}\).

Kẻ \(BH\bot AD\), ta có \(AH=HD=3\,cm\) (vì \(BH\) là đường cao đồng thời là trung tuyến)

Áp dụng định lí Pytago vào tam giác vuông \(ABH\), ta có

\(B{H^2} = A{B^2} - A{H^2}=6^2-3^2=27\) nên \( BH = 3\sqrt3\) (cm)

\({S_{ABCD}}= AD.BH = 6.3\sqrt 3\)\(\,= 18\sqrt 3\;(c{m^2})\)

Loigiaihay.com