Bài 23 trang 128 Vở bài tập toán 9 tập 1

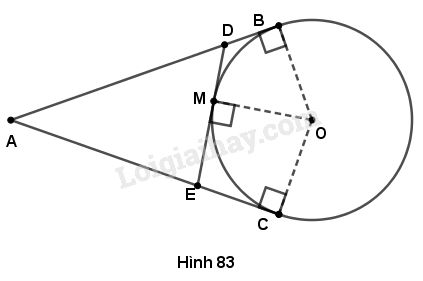
Đề bài

Từ một điểm \(A\) nằm bên ngoài đường tròn \((O)\), kẻ các tiếp tuyến \(AB,\ AC\) với đường tròn (\(B,\ C\) là các tiếp điểm). Qua điểm \(M\) thuộc cung nhỏ \(BC\), kẻ tiếp tuyến với đường tròn \(O\), nó cắt các tiếp tuyến \(AB\) và \(AC\) theo thứ tự ở \(D\) và \(E\). Chứng minh rằng chu vi tam giác \(ADE\) bằng \(2AB\). 

Lời giải chi tiết

Chu vi tam giác \(ADE\) bằng \(AD + DE + AE \) \(= AD + DM + ME + AE\,{\rm{   (1)}}\)

Theo tính chất của hai tiếp tuyến cắt nhau, ta có

\(DM = DB\,{\rm{                       (2)}}\)

\(ME = EC{\rm{                        }}\left( 3 \right)\)

Từ \(\left( 1 \right);\left( 2 \right);\left( 3 \right)\) suy ra

\(AD + DM + ME + AE \)\(= AD + BD + EC + AE\)\( = AB + AC\)

Ta lại có \(AB = AC\) nên chu vi tam giác \(ADE\) bằng \(2AB.\)

Loigiaihay.com