Bài 23 trang 108 Vở bài tập toán 8 tập 1

Đề bài

Dựng hình thang \(ABCD\), biết \(\widehat D = {90^o}\), đáy \(CD = 3cm\), cạnh bên \(AD = 2cm\), cạnh bên \(BC = 3cm\). 

Lời giải chi tiết

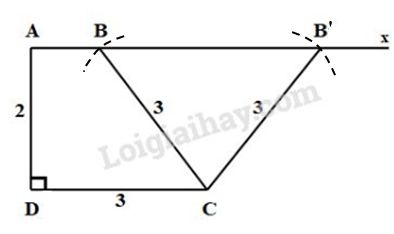
Cách dựng: 

- Dựng \(\Delta ADC\) có \(\widehat D = {90^o}\), \(DA = 2cm,\) \(DC = 3cm, \)

- Dựng tia \(Ax // CD\) (tia \(Ax\) nằm trên nửa mặt phẳng bờ \(AD\) chứa điểm \(C\)).

- Dựng cung tròn tâm \(C\) bán kính \(3\,cm\) cắt tia \(Ax\) tại hai điểm \(B\) và \(B'\).

- Dựng đoạn thẳng \(BC;\;B'C.\)

Chứng minh:

Tứ giác \(ABCD\) có \(AB//CD\) nên là hình thang. Hình thang \(ABCD\) có \(\widehat D = {90^o},\) \(CD = 3cm,\) \(AD = 2cm,\) \(BC = 3cm\) nên hình thang \(ABCD\) thỏa mãn điều kiện bài toán.

Lưu ý:

a) Ta đã biết cách dựng tam giác biết hai cạnh và góc xen giữa, do đó không cần trình bày từng bước dựng \(\Delta ACD.\)

b) Trong bài trên, có hai hình thang thỏa mãn đề bài là \(ABCD\) và \(AB'CD\).

Loigiaihay.com