Giải bài 2.29 trang 28 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

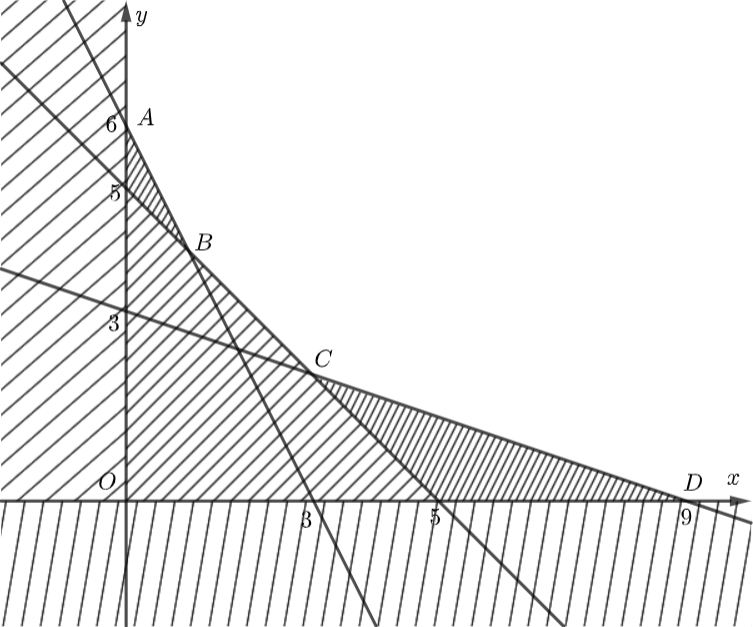
Đề bài

Giả sử một người ăn kiêng cần được cung cấp ít nhất 300 calo, 36 đơn vị vitamin A và 90 đơn vị vitamin C mỗi ngày từ hai loại đồ uống / và //. Mỗi cốc đồ uống / cung cấp 60 calo, 12 đơn vị vitamin A và 10 đơn vị vitamin C.

Mỗi cốc đồ uống // cung cấp 60 calo, 6 đơn vị vitamin A và 30 đơn vị vitamin C. Biết rằng một cốc đồ uống / có giá 12 nghìn đồng và một cốc đồ uống // có giá 15 nghìn đồng.

a) Gọi x và y tương ứng là số cốc đồ uống / và //. Viết các phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình và xác định miền nghiệm của hệ đó.

b) Gọi F (nghìn đồng) là số tiền phải trả cho x cốc đồ uống / và y là số tiền phải trả cho y cốc đồ uống //. Hãy biểu diễn F theo x và y.

c) Biết rằng F đạt giá trị nhỏ nhất trên miền nghiệm tìm được ở câu a tại một trong các đỉnh của miền nghiệm, tìm giá trị nhỏ nhất đó. Từ đó suy ra người đó cần uống bao nhiêu cốc loại / và loại // để chi phí là nhỏ nhất. mà vẫn đáp ứng được yêu cầu hằng ngày.

Lời giải chi tiết

a) Gọi x và y tương ứng là số cốc đồ uống / và //.

Điều kiện: \(x \ge 0;\,\,y \ge 0.\)

Số calo cần cung cấp cho người ăn kiêng từ hai loại đồ uống / và // là: \(60x + 60y \ge 300\,\, \Leftrightarrow \,\,x + y \ge 5.\)

Số vitamin A cần cung cấp cho người ăn kiêng từ hai loại đồ uống / và // là: \(12x + 6y \ge 36\,\, \Leftrightarrow \,\,2x + y \ge 6.\)

Số vitamin C cần cung cấp cho người ăn kiêng từ hai loại đồ uống / và // là: \(10x + 30y \ge 90\,\, \Leftrightarrow \,\,x + 3y \ge 9.\)

Ta có hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{x + y \ge 5}\\{2x + y \ge 6}\\{x + 3y \ge 9}\end{array}.} \right.\)

Miền nghiệm của bất phương trình \(d:x \ge 0\) là nửa mặt phẳng bờ \(d\) chứa điểm \(\left( {1;0} \right).\)

Miền nghiệm của bất phương trình \({d_1}:y \ge 0\) là nửa mặt phẳng bờ \({d_1}\) chứa điểm \(\left( {0;1} \right).\)

Miền nghiệm của bất phương trình \(x + y \ge 5\) là nửa mặt phẳng bờ \({d_2}:x + y = 5\) không chứa gốc tọa độ \(O\left( {0;0} \right).\)

Miền nghiệm của bất phương trình \(2x + y \ge 6\) là nửa mặt phẳng bờ \({d_3}:2x + y = 6\) không chứa gốc tọa độ \(O\left( {0;0} \right).\)

Miền nghiệm của bất phương trình \(x + 3y \ge 9\) là nửa mặt phẳng bờ \({d_4}:x + 3y = 9\) không chứa gốc tọa độ \(O\left( {0;0} \right).\)

 

Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{x + y \ge 5}\\{2x + y \ge 6}\\{x + 3y \ge 9}\end{array}} \right.\)là miền không bị gạch với \(A\left( {0;6} \right),\,\,B\left( {1;4} \right),\,\,C\left( {3;2} \right),\,\,D\left( {9;0} \right).\)

b) Số tiền phải trả cho hai loại đồ uống / và // là: \(F\left( {x;y} \right) = 12x + 15y\) (nghìn đồng).

c) Ta có: \(F\left( {0;6} \right) = 12.0 + 15.6 = 90,\,\,F\left( {1;4} \right) = 12.1 + 15.4 = 72,\)

\(F\left( {3;2} \right) = 12.3 + 15.2 = 66,\,\,F\left( {9;0} \right) = 12.9 + 15.0 = 108.\)

\( \Rightarrow \) Giá trị nhỏ nhất của \(F\) là \(F\left( {3;2} \right) = 66.\)

Vậy người đó cần uống 3 cốc đồ uống loại / và 2 cốc đồ uống loại // để đáp úng yêu cầu đặt ra hàng ngày.