Giải bài 2 trang 115 SGK Toán 8 tập 1 - Cánh diều

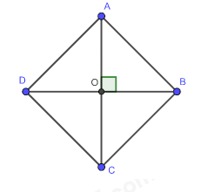
Đề bài

Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Chứng minh:

\(A{C^2} + B{{\rm{D}}^2} = 4\left( {O{A^2} + O{B^2}} \right) = 4{\rm{A}}{B^2}\)

Lời giải chi tiết

Xét \(\Delta OAB\) vuông tại A có: \(O{A^2} + O{B^2} = A{B^2}\)

Vì ABCD là hình thoi nên OA = OC; OB = OD

Ta có:

\(\begin{array}{l}A{C^2} + B{D^2} = {(OA + OC)^2} + {(OB + OD)^2}\\ = {(OA + OA)^2} + {(OB + OB)^2}\\ = {(2OA)^2} + {(2OB)^2} = 4.O{A^2} + 4.O{B^2} = 4{(OA^2 + OB^2)} = 4.A{B^2}\end{array}\)