Giải Bài 13 trang 93 sách bài tập toán 7 tập 1 - Cánh diều

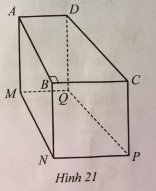
Đề bài

Cho hình lăng trụ đứng tứ giác ABCD.MNPQ có đáy là hình thang vuông ABCD vuông tại B (AD song song với BC) với \(AB = 20{\rm{ cm}}\), \(AD = 11{\rm{ cm}}\), \(BC = 15{\rm{ cm}}\) (Hình 21).

a) Tính tỉ số giữa thể tích của hình lăng trụ đứng tam giác ABC.MNP và thể tích của hình lăng trụ đứng tứ giác ABCD.MNPQ.

b) Tính tỉ số phần trăm giữa thể tích của hình lăng trụ đứng tam giác ABD.MNQ và thể tích của hình lăng trụ đứng tam giác BCD.NPQ.

c) So sánh thể tích của hai hình lăng trụ đứng tam giác ABD.MNQ và ACD.MPQ.

Lời giải chi tiết

a) Ta có:

\({S_{ABC}} = \dfrac{{20{\rm{ }}.{\rm{ }}15}}{2} = 150{\rm{ (c}}{{\rm{m}}^2});\\{S_{ABCD}} = \dfrac{{(11 + 15){\rm{ }}.{\rm{ }}20}}{2} = 260{\rm{ (c}}{{\rm{m}}^2}).\)

Tỉ số giữa thể tích của hình lăng trụ đứng tam giác ABC.MNP và thể tích của hình lăng trụ đứng tứ giác ABCD.MNPQ là:

\(\dfrac{{{V_{ABC.MNP}}}}{{{V_{ABCD.MNPQ}}}} = \dfrac{{{S_{ABC}}{\rm{ }}.{\rm{ }}BN}}{{{S_{ABCD}}{\rm{ }}.{\rm{ }}BN}} \\= \dfrac{{{S_{ABC}}}}{{{S_{ABCD}}}} = \dfrac{{150}}{{260}} = \dfrac{{15}}{{26}}.\)

b) Ta có:

\({S_{ABD}} = \dfrac{{20{\rm{ }}.{\rm{ }}11}}{2} = 110{\rm{ (c}}{{\rm{m}}^2});\\{S_{BCD}} = \dfrac{{15{\rm{ }}.{\rm{ }}20}}{2} = 150{\rm{ (c}}{{\rm{m}}^2}).\)

Tỉ số phần trăm giữa thể tích của hình lăng trụ đứng tam giác ABD.MNQ và thể tích của hình lăng trụ đứng tam giác BCD.NPQ là:

\(\dfrac{{{V_{ABD.MNQ}}{\rm{ }}.{\rm{ }}100\% }}{{{V_{BCD.NPQ}}}} = \dfrac{{{S_{ABD}}{\rm{ }}.{\rm{ }}BN{\rm{ }}.{\rm{ }}100\% }}{{{S_{BCD}}{\rm{ }}.{\rm{ }}BN}} \\ = \dfrac{{{S_{ABD}}{\rm{ }}.{\rm{ }}100\% }}{{{S_{BCD}}}} = \dfrac{{110{\rm{ }}.{\rm{ }}100\% }}{{150}} = 73,(3)\% .\)

c) Ta có:

\({S_{ABC}} = 150{\rm{ (c}}{{\rm{m}}^2});\\{S_{ACD}} = {S_{ABCD}} - {S_{ABC}} = 260 - 150 = 110{\rm{ (c}}{{\rm{m}}^2}).\)

\({S_{ABD}} = 110{\rm{ (c}}{{\rm{m}}^2})\).

Suy ra:

\(\begin{array}{l}{S_{ACD}} = {S_{ABD}}\\ \Rightarrow {S_{ACD}}{\rm{ }}.{\rm{ }}BN = {S_{ABD}}{\rm{ }}.{\rm{ }}BN\\ \Rightarrow {V_{ABD.MNQ}} = {V_{ACD.MPQ}}\end{array}\)

Vậy thể tích của hai hình lăng trụ đứng tam giác ABD.MNQ và ACD.MPQ bằng nhau.