Bài 13 trang 61 Vở bài tập toán 9 tập 1

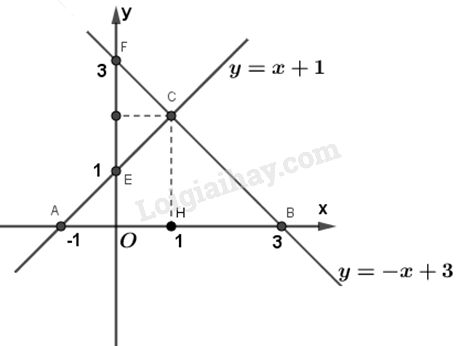
Đề bài

a) Vẽ đồ thị của các hàm số y = x + 1 và y = -x + 3 trên cùng một mặt phẳng tọa độ.

b) Hai đường thẳng y = x + 1 và y = -x + 3 cắt nhau tại C và cắt trục Ox theo thứ tự A và B. Tìm tọa độ của các điểm A, B, C.

c) Tính chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimet).

Lời giải chi tiết

a) 

- Vẽ đường thẳng đi qua hai điểm \(E\left( {0;1} \right)\) và \(A\left( { - 1;0} \right)\) ta được đồ thị của hàm số \(y = x + 1\).

- Vẽ đường thẳng đi qua hai điểm \(F\left( {0;3} \right)\) và \(B\left( {3;0} \right)\) thì ta được đồ thị của hàm số \(y =  - x + 3\).

b)

- Đường thẳng \(y = x + 1\) cắt trục hoành tại điểm \(A\left( { - 1;0} \right)\).

- Đường thẳng \(y =  - x + 3\) cắt trục hoành tại điểm \(B\left( {3;0} \right)\).

- Từ \(x + 1 =  - x + 3\) ta có \(x = 1\)

Thay \(x = 1\) vào một trong hai hàm số đã cho ta tính được \(y = 2\)

Vậy tọa độ của điểm C là \(C\left( {1;2} \right)\)

c)

Gọi P là chu vi của tam giác ABC và S là diện tích của tam giác ABC.

Ta có : \(AC = \sqrt {H{A^2} + H{C^2}} ;BC = \sqrt {H{B^2} + H{C^2}} \)

Vậy \(P = AC + BC + AB\)

           \( = \sqrt {{2^2} + {2^2}}  + \sqrt {{2^2} + {2^2}}  + 4\)

           \( = 4\sqrt 2  + 4\)

            \( = 4\left( {\sqrt 2  + 1} \right)\left( {cm} \right)\)

Tính trên máy tính cầm tay ta được \(P = 4\sqrt 2  + 4 \approx 9,66\left( {cm} \right)\)

\(S = \dfrac{1}{2}AB \cdot CH = \dfrac{1}{2} \cdot 4 \cdot 2 = 4\left( {c{m^2}} \right)\)

Loigiaihay.com