Bài 12 trang 60 Vở bài tập toán 9 tập 1

Đề bài

a) Vẽ đồ thị của các hàm số y = x và y = 2x + 2 trên cùng một mặt phẳng tọa độ.

b) Gọi A là giao điểm của hai đồ thị nói trên, tìm tọa độ điểm A.

c) Vẽ qua điểm B(0 ; 2) một đường thẳng song song với trục Ox, cắt đường thẳng y = x tại điểm C. Tìm tọa độ của điểm C rồi tính diện tích tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét).

Lời giải chi tiết

a) 

 

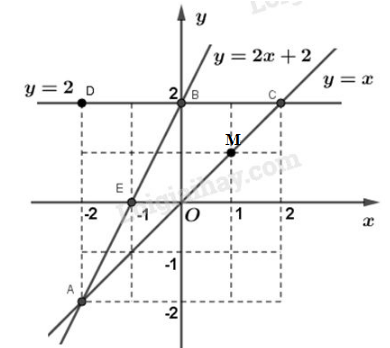
Vẽ đường thẳng đi qua hai điểm \(O\left( {0;0} \right)\) và \(M\left( {1;1} \right)\) ta được đồ thị của hàm số \(y = x\).

Vẽ đường thẳng đi qua hai điểm \(B\left( {0;2} \right)\) và \(E\left( { - 1;0} \right)\) ta được đồ thị của hàm số \(y = 2x + 2\).

b) Hoành độ giao điểm của hai đồ thị hàm số đã cho là nghiệm của phương trình:

\(2x + 2 = x \Leftrightarrow x =  - 2\)

Thay \(x =  - 2\) vào một trong hai hàm số ta tính được tung độ của A là \(y =  - 2\)

Vậy đồ thị hai hàm số đã cho cắt nhau tại \(A\left( { - 2; - 2} \right)\).

c) Qua điểm \(B\left( {0;2} \right)\) vẽ đường thẳng song song với \(Ox\), đường thẳng này có phương trình \(y = 2\), cắt đường thẳng \(y = x\) tại điểm C.

- Tọa độ của điểm C :

Với \(y = x\) mà \(y = 2\) nên \(x = 2\). Ta có \(C\left( {2;2} \right)\)

- Diện tích tam giác ABC:

Tam giác ABC có cạnh đáy là BC và chiều cao là AD.

\(BC = 2cm\) và \(AD = 4cm.\)

Vậy \({S_{ABC}} = \dfrac{1}{2}BC \cdot AD = \dfrac{1}{2} \cdot 2 \cdot 4 = 4\left( {c{m^2}} \right)\)

Loigiaihay.com