Giải mục 1 trang 44, 45, 46 Chuyên đề học tập Toán 11 Chân trời sáng tạoSử dụng sơ đồ ở Hình 1 để trả lời các câu hỏi dưới đây: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Khám phá 1
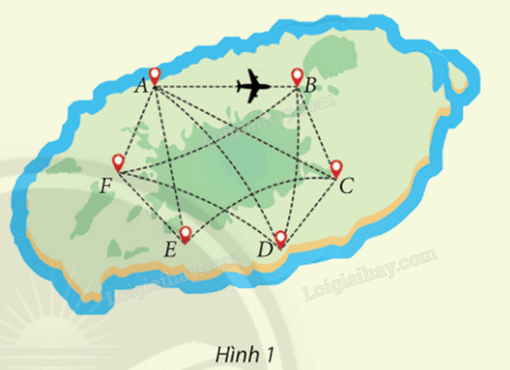
Sử dụng sơ đồ ở Hình 1 để trả lời các câu hỏi dưới đây: a) Từ thành phố A, hãng X có bao nhiêu đường bay đến năm thành phố còn lại? b) Giữa sáu thành phố trên, có tất cả bao nhiêu đường bay của hãng X? c) Có thể giải đáp thắc mắc ở Hoạt động khởi động không? Phương pháp giải: Quan sát hình 1 để trả lời câu hỏi Lời giải chi tiết: a) Quan sát sơ đồ ở Hình 1, ta thấy: ⦁ Có 1 đường bay từ thành phố A đến thành phố B; ⦁ Có 1 đường bay từ thành phố A đến thành phố D; ⦁ Có 1 đường bay từ thành phố A đến thành phố E; ⦁ Có 1 đường bay từ thành phố A đến thành phố F. Vậy từ thành phố A, hãng X có tất cả 4 đường bay đến năm thành phố còn lại. b)Vì đường bay của hãng X là đường bay hai chiều nên đường bay từ thành phố B đến thành phố A đã được tính vào đường bay từ thành phố A đến thành phố B. Do đó từ thành phố B, hãng X có thêm: ⦁ 1 đường bay đến thành phố C; ⦁ 1 đường bay đến thành phố D; ⦁ 1 đường bay đến thành phố F. Khi đó, từ thành phố B, hãng X có thêm 3 đường bay đến năm thành phố còn lại. Tương tự như vậy, ta được: – Từ thành phố C, hãng X có thêm 2 đường bay đến năm thành phố còn lại; – Từ thành phố D, hãng X có thêm 1 đường bay đến năm thành phố còn lại; – Từ thành phố E, hãng X có thêm 1 đường bay đến năm thành phố còn lại. Vì đường bay của hãng X là đường bay hai chiều nên đường bay từ thành phố F đến năm thành phố còn lại đã được tính vào các đường bay kể trên. Vậy giữa sáu thành phố trên, có tất cả 4 + 3 + 2 + 1 + 1 = 11 đường bay của hãng X. Chú ý: Ngoài cách trên, ta có thể đếm số đường cong và đường thẳng (thể hiện đường bay) trên Hình 1 (hoặc Bảng 1) để kết luận về số đường bay của hãng X. c) Ta có thể giải đáp thắc mắc ở Hoạt động khởi động như sau: Bước 1: Từ thành phố A bay đến thành phố B; Bước 2: Từ thành phố B bay đến thành phố C; Bước 3: Từ thành phố C bay đến thành phố D; Bước 4: Từ thành phố D bay đến thành phố F; Bước 5: Từ thành phố F bay đến thành phố E; Bước 6: Từ thành phố E bay về thành phố A. Vậy từ thành phố A, ta có thể thăm năm thành phố B, C, D, E và F bằng các chuyến bay của hãng X sao cho mỗi thành phố chỉ qua đúng một lần, rồi quay trở về A. Chú ý: Ta có thể thay đổi thứ tự bay đến các thành phố chỉ cần hãng X có chuyến bay giữa hai thành phố liền kề. Thực hành 1 Cho đồ thị G như Hình 5. a) Chỉ ra các đỉnh, các cạnh, số đỉnh, số cạnh của G. b) Chỉ ra các đỉnh kề đỉnh D, các đỉnh kề đỉnh B. c) Đồ thị G có đỉnh cô lập không?
Phương pháp giải: Đồ thị G là hình bao gồm: - Tập hợp hữu hạn các điểm, mỗi điểm gọi là một đỉnh của đồ thị. - Tập hợp các đoạn (cong hoặc thẳng), mỗi đoạn nối 2 đỉnh gọi là cạnh của đồ thị. Lời giải chi tiết:
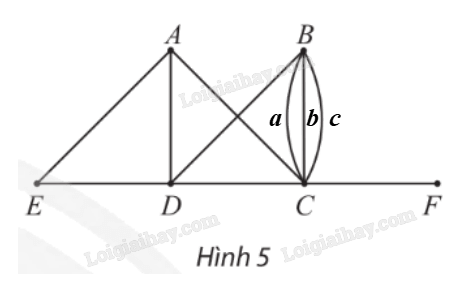
a) Các đỉnh của đồ thị G là: A, B, C, D, E và F. Đồ thị có 6 đỉnh. Các cạnh của đồ thị G là: AC, AD, AE, a, b, c, BD, CD, CF, DE. Đồ thị có 10 cạnh. b) Các đỉnh kề đỉnh D là: A, B, C, E. Các đỉnh kề đỉnh B là: C, D. c) Đồ thị G không có đỉnh cô lập. Vận dụng 1 Một mạng cục bộ có bảy máy tính 1; 2; 3; 4; 5; 6 và 7. Bảng 2 cho biết giữa mỗi cặp máy tính có kết nối trực tiếp với nhau hay không (dấu ✔ là có kết nối, dấu ✘ là không kết nối). Hãy vẽ đồ thị biểu diễn sự kết nối giữa các máy tính của mạng này.
Phương pháp giải: Dựa vào bảng 2 để vẽ đồ thị Lời giải chi tiết: Ta vẽ đồ thị G có 7 đỉnh A, B, C, D, E, F, G lần lượt biểu diễn bảy máy tính 1; 2; 3; 4; 5; 6 và 7. Hai đỉnh được nối bằng một cạnh nếu giữa hai máy tính có kết nối trực tiếp với nhau. Ta có đồ thị G như sau:
|























Danh sách bình luận