Đề thi học kì 2 môn toán lớp 7 năm 2019 - 2020 trường THCS Trần Văn ƠnGiải chi tiết đề thi học kì 2 môn toán lớp 7 năm 2019 - 2020 trường THCS Trần Văn Ơn với cách giải nhanh và chú ý quan trọng Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
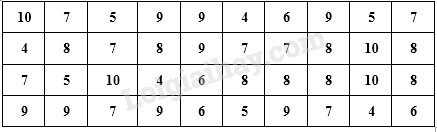
Câu 1 (1,5 điểm): Điểm kiểm tra môn Toán của tất cả học sinh lớp 7A được ghi lại qua bảng sau:
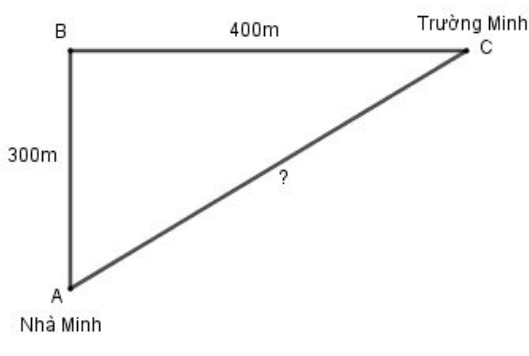
Lập bảng “tần số” để tìm số trung bình cộng và tìm Mốt của dấu hiệu. Câu 2 (2 điểm): a) Thu gọn rồi tìm bậc của đơn thức \(P = {\left( {\dfrac{2}{5}{x^2}{y^3}} \right)^2}.\left( {\dfrac{{ - 25}}{8}x{y^2}{z^2}} \right)\) b) Thu gọn đa thức \(M = 3{x^2}y - 4{x^2} - 2{x^2}y\) \( + 6 - 6xy - 5{x^2}y + {x^2}\) Câu 3 (2 điểm): Cho hai đa thức \(\begin{array}{l}A\left( x \right) = 3x - 2{x^3} + 6 + 4{x^2}\\B\left( x \right) = 3{x^2} - 3x + 2{x^3} + 2\end{array}\) a) Tính \(C\left( x \right) = A\left( x \right) + B\left( x \right)\) và \(D\left( x \right) = A\left( x \right) - B\left( x \right)\). b) Chứng tỏ rằng \(x = 0\) không phải là nghiệm của \(C\left( x \right)\). Câu 4 (1,5 điểm): a) Một khu vườn hình chữ nhật có chiều rộng \(x\,\left( m \right)\), chiều dài hơn chiều rộng \(3\,m\). Hãy viết biểu thức đại số biểu thị chu vi khu vườn hình chữ nhật rồi tính chu vi của khu vườn đó khi \(x = 5\,\left( m \right)\). b) Bạn Minh từ nhà đi thẳng \(300\,m\) tới ngã tư rồi rẽ phải và đi thêm \(400\,m\) nữa thì đến trường. Hãy tính khoảng cách theo đường chim bay từ nhà bạn Minh đến trường.
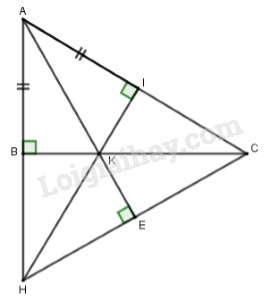
Câu 5 (3 điểm): Cho tam giác \(ABC\) vuông tại \(B\) \(\left( {BA < BC} \right)\). Trên cạnh \(AC\) lấy điểm \(I\) sao cho \(AB = AI\), qua \(I\) vẽ đường thẳng vuông góc với \(AC\) cắt \(BC\) tại \(K\). a) Chứng minh \(\Delta ABK = \Delta AIK\). b) Kéo dài \(AB\) và \(IK\) cắt nhau tại \(H\). Chứng minh \(\Delta AIH = \Delta ABC\) rồi suy ra \(\Delta AHC\) cân. c) Vẽ \(KE\) vuông góc \(HC\) tại \(E\). Chứng minh ba điểm \(A,K,E\) thẳng hàng. HẾT LG câu 1 Phương pháp giải: Quan sát bảng số liệu để lập bảng tần số Tần số của giá trị là số lần xuất hiện của giá trị đó trong bảng số liệu Mốt của dấu hiệu là giá trị có tần số lớn nhất Cách tìm số trung bình cộng: \(\overline M = \dfrac{{{x_1}{n_1} + {x_2}{n_2} + ... + {x_k}{n_k}}}{N}\) Với \({x_1};{x_2};...;{x_k}\) là các giá trị của dấu hiệu \({n_1};{n_2};...;{n_k}\) là tần số tương ứng của các giá trị \({x_1};{x_2};...;{x_k}\) \(N\) là tổng các tần số Lời giải chi tiết: Bảng tần số
Số trung bình cộng : \(\overline M \) \( = \dfrac{{4.4 + 5.4 + 6.4 + 7.8 + 8.8 + 9.8 + 10.4}}{{40}}\)\( = \dfrac{{292}}{{40}} = 7,3\) Mốt của dấu hiệu là \({M_0} = 7;{M_0} = 8;{M_0} = 9\) (vì các giá trị này có cùng tần số lớn nhất là \(8\)) LG câu 2 Phương pháp giải: a) Muốn nhân đơn thức với đơn thức ta nhân phần hệ số với nhau và phần biến số với nhau b) Để thu gọn đa thức ta nhóm các đơn thức đồng dạng rồi tính toán Lời giải chi tiết: a) Thu gọn rồi tìm bậc của đơn thức \(P = {\left( {\dfrac{2}{5}{x^2}{y^3}} \right)^2}.\left( {\dfrac{{ - 25}}{8}x{y^2}{z^2}} \right)\) Ta có: \(P = {\left( {\dfrac{2}{5}{x^2}{y^3}} \right)^2}.\left( {\dfrac{{ - 25}}{8}x{y^2}{z^2}} \right)\) \(\begin{array}{l} = {\left( {\dfrac{2}{5}} \right)^2}.{\left( {{x^2}} \right)^2}.{\left( {{y^3}} \right)^2}.\left( {\dfrac{{ - 25}}{8}x{y^2}{z^2}} \right)\\ = \dfrac{4}{{25}}.{x^4}{y^6}.\left( {\dfrac{{ - 25}}{8}x{y^2}{z^2}} \right)\\ = \left( {\dfrac{4}{{25}}.\dfrac{{ - 25}}{8}} \right).\left( {{x^4}.x} \right).\left( {{y^6}.{y^2}} \right).{z^2}\\ = \dfrac{{ - 1}}{2}.{x^{4 + 1}}.{y^{6 + 2}}.{z^2}\\ = \dfrac{{ - 1}}{2}{x^5}{y^8}{z^2}\end{array}\) Vậy \(P = - \dfrac{1}{2}{x^5}{y^8}{z^2}\) b) Thu gọn đa thức \(M = 3{x^2}y - 4{x^2} - 2{x^2}y\) \( + 6 - 6xy - 5{x^2}y + {x^2}\) Ta có: \(M = 3{x^2}y - 4{x^2} - 2{x^2}y\) \( + 6 - 6xy - 5{x^2}y + {x^2}\) \( = \;\left( {3{x^2}y - 2{x^2}y - 5{x^2}y} \right)\) \( + \left( { - 4{x^2} + {x^2}} \right) - 6xy + 6\) \( = {x^2}y\left( {3 - 2 - 5} \right)\) \( + {x^2}\left( { - 4 + 1} \right) - 6xy + 6\) \( = - 4{x^2}y - 3{x^2} - 6xy + 6\) Vậy \(M = - 4{x^2}y - 3{x^2} - 6xy + 6\) LG câu 3 Phương pháp giải: a) Để cộng trừ các đa thức một biến ta thu gọn và sắp xếp các đa thức (nếu cần), sau đó đặt phép tính theo hàng ngang (hoặc hàng dọc), phá ngoặc rồi cộng trừ các đơn thức đồng dạng với nhau b) \(x = {x_0}\) không là nghiệm của đa thức \(P\left( x \right)\) khi \(P\left( {{x_0}} \right) \ne 0\) Lời giải chi tiết: Cho hai đa thức \(\begin{array}{l}A\left( x \right) = 3x - 2{x^3} + 6 + 4{x^2}\\B\left( x \right) = 3{x^2} - 3x + 2{x^3} + 2\end{array}\) a) Tính \(C\left( x \right) = A\left( x \right) + B\left( x \right)\) và \(D\left( x \right) = A\left( x \right) - B\left( x \right)\). \(\begin{array}{l}A\left( x \right) = 3x - 2{x^3} + 6 + 4{x^2}\\ = - 2{x^3} + 4{x^2} + 3x + 6\end{array}\) \(\begin{array}{l}B\left( x \right) = 3{x^2} - 3x + 2{x^3} + 2\\ = 2{x^3} + 3{x^2} - 3x + 2\end{array}\) Ta có: \(C\left( x \right) = A\left( x \right) + B\left( x \right)\) \( = - 2{x^3} + 4{x^2} + 3x + 6\)\( + \left( {2{x^3} + 3{x^2} - 3x + 2} \right)\) \( = - 2{x^3} + 4{x^2} + 3x + 6\) \( + 2{x^3} + 3{x^2} - 3x + 2\) \( = \left( { - 2{x^3} + 2{x^3}} \right) + \left( {4{x^2} + 3{x^2}} \right)\) \( + \left( {3x - 3x} \right) + 6 + 2\) \( = 7{x^2} + 8\) Vậy \(C\left( x \right) = 7{x^2} + 8\) \(D\left( x \right) = A\left( x \right) - B\left( x \right)\) \( = - 2{x^3} + 4{x^2} + 3x + 6\)\( - \left( {2{x^3} + 3{x^2} - 3x + 2} \right)\) \( = - 2{x^3} + 4{x^2} + 3x + 6\) \( - 2{x^3} - 3{x^2} + 3x - 2\) \( = \left( { - 2{x^3} - 2{x^3}} \right) + \left( {4{x^2} - 3{x^2}} \right)\) \( + \left( {3x + 3x} \right) + 6 - 2\) \( = - 6{x^3} + {x^2} + 6x + 4\) Vậy \(D\left( x \right) = \)\( - 6{x^3} + {x^2} + 6x + 4\) b) Chứng tỏ rằng \(x = 0\) không phải là nghiệm của \(C\left( x \right)\). Thay \(x = 0\) vào \(C\left( x \right) = 7{x^2} + 8\) ta được: \(C\left( 0 \right) = {7.0^2} + 8\) \( = 8 \ne 0\) nên \(x = 0\) không phải là nghiệm của \(C\left( x \right)\). LG câu 4 Phương pháp giải: a) Chu vi hình chữ nhật bằng hai lần tổng chiều dài và chiều rộng b) Sử dụng định lý Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông Lời giải chi tiết: a) Một khu vườn hình chữ nhật có chiều rộng \(x\,\left( m \right)\), chiều dài hơn chiều rộng \(3\,m\). Hãy viết biểu thức đại số biểu thị chu vi khu vườn hình chữ nhật rồi tính chu vi của khu vườn đó khi \(x = 5\,\left( m \right)\). Chu vi khu vườn hình chữ nhật là: \(C\left( x \right) = \left( {x + x + 3} \right).2 = 4x+6\) Khi \(x = 5\) thì chu vi khu vườn là \(C\left( 5 \right) = \left( {4.5 + 6} \right).2 = 52{m^2}\) b) Bạn Minh từ nhà đi thẳng \(300\,m\) tới ngã tư rồi rẽ phải và đi thêm \(400\,m\) nữa thì đến trường. Hãy tính khoảng cách theo đường chim bay từ nhà bạn Minh đến trường. Xét tam giác ABC vuông tại B, theo định lý Pytago ta có: \(A{C^2} = B{C^2} + A{B^2}\) \( = {300^2} + {400^2} = 250000\) Suy ra \(AC = 500m\) Vậy khoảng cách đường chim bay từ nhà bạn Minh đến trường là 500m. LG câu 5 Phương pháp giải: a) Chứng minh hai tam giác vuông bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông. b) Chứng minh hai tam giác \(AIH\) và \(ABC\) bằng nhau theo trường hợp cạnh góc vuông – góc nhọn) c) Chứng minh \(AK \bot HC\) và \(KE \bot HC\) rồi suy ra ba điểm \(A,K,E\) thẳng hàng. Lời giải chi tiết: Cho tam giác \(ABC\) vuông tại \(B\) \(\left( {BA < BC} \right)\). Trên cạnh \(AC\) lấy điểm \(I\) sao cho \(AB = AI\), qua \(I\) vẽ đường thẳng vuông góc với \(AC\) cắt \(BC\) tại \(K\).
a) Chứng minh \(\Delta ABK = \Delta AIK\). Tam giác \(ABC\) vuông tại \(B\) nên \(\widehat {ABC} = {90^0}\). \(KI \bot AC\) nên \(\widehat {AIK} = {90^0}\). Xét \(\Delta ABK\) và \(\Delta AIK\) có: \(\widehat {ABK} = \widehat {AIK} = {90^0}\) \(AK\) chung \(AB = AI\left( {gt} \right)\) \( \Rightarrow \Delta ABK = \Delta AIK\) (cạnh huyền – cạnh góc vuông) (đpcm). b) Kéo dài \(AB\) và \(IK\) cắt nhau tại \(H\). Chứng minh \(\Delta AIH = \Delta ABC\) rồi suy ra \(\Delta AHC\) cân. Xét \(\Delta AIH\) và \(\Delta ABC\) có: \(\begin{array}{l}\widehat {AIH} = \widehat {ABC} = {90^0}\\AI = AB\left( {gt} \right)\\\widehat A\,\,\,chung\end{array}\) \( \Rightarrow \Delta AIH = \Delta ABC\) (cạnh góc vuông – góc nhọn) \( \Rightarrow AH = AC\) (cạnh tương ứng) Tam giác \(AHC\) có \(AH = AC\left( {cmt} \right)\) nên là tam giác cân tại \(A\) (đpcm). c) Vẽ \(KE\) vuông góc \(HC\) tại \(E\). Chứng minh ba điểm \(A,K,E\) thẳng hàng. Xét tam giác \(AHC\) có: \(HI \bot AC,CB \bot AH\) nên \(HI\) và \(CB\) là các đường cao cắt nhau tại \(K\). Do đó \(K\) là trực tâm \(\Delta AHC\) \( \Rightarrow AK \bot HC\,\,\,\left( 1 \right)\). Lại có \(KE \bot HC\,\,\,\left( 2 \right)\). Mà qua điểm \(K\) chỉ có duy nhất \(1\) đường thẳng vuông góc với \(HC\) nên từ (1) và (2) suy ra \(A,K,E\) thẳng hàng (đpcm) HẾT Loigiaihay.com
|





















Danh sách bình luận