Đề thi học kì 2 môn toán lớp 7 năm 2019 - 2020 trường THCS Giảng Võ

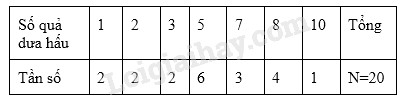
Đề bài

Bài 1  (2,5 điểm):

Trong đợt bán “giải cứu dưa hấu”, một cửa hàng thống kê số quả dưa hấu bán cho 20 khách hàng đầu tiên như sau:

a) Dấu hiệu cần tìm hiểu ở đây là gì? 

b) Lập bảng “tần số”, tìm trung bình cộng và mốt của dấu hiệu.

c) Vẽ biểu đồ đoạn thẳng. (Trục hoành biểu diễn số quả dưa hấu của một người mua, trục tung biểu diễn tần số)

Bài 2 (1,5 điểm):

Cho đơn thức \(D = 5{x^4}y.\left( { - \dfrac{3}{{10}}x{y^2}} \right)\)

a) Thu gọn, xác định hệ số và bậc của đơn thức \(D\).

b) Tính giá trị của đơn thức \(D\) biết \(x =  - 1;y = \dfrac{1}{3}\).

Bài 3 (2,5 điểm):

Cho hai đa thức \(M\left( x \right) = 2{x^4} + 2{x^3}\) \( - 5x - 10 + 3{x^2} + 2{x^3}\)

\(N\left( x \right) = 4{x^4} - 7 + 4{x^3} - 2{x^4} - 5x + 9\)

a) Thu gọn đa thức \(M\left( x \right);N\left( x \right)\) và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm dần của biến.

b) Tính \(M\left( x \right) + N\left( x \right)\).

c) Tính \(Q\left( x \right) = M\left( x \right) - N\left( x \right)\) và tìm nghiệm của đa thức \(Q\left( x \right)\).

Bài 4 (3,5 điểm):

Cho tam giác MNP vuông tại M có \(MN < MP\), \(A\) là trung điểm của \(NP\). Đường trung trực của đoạn thẳng \(NP\) cắt cạnh \(MP\) tại \(B\).

a) Chứng minh tam giác BNP cân, từ đó so sánh BM và BP.

b) Qua P kẻ đường vuông góc với đường thẳng NB tại điểm C. Chứng minh tam giác MBN bằng tam giác CBP.

c) Chứng minh AB là tia phân giác của góc MAC.

d) Gọi E là giao điểm của AB và tia PC. Tam giác MNP cần có thêm điều kiện gì để tam giác EBP cân tại B?

LG bài 1

Phương pháp giải:

a) Dấu hiệu là vấn đề hay hiện tượng mà người điều tra quan tâm tìm hiểu.

b) Liệt kê các giá trị khác nhau của số quả dưa hấu bán cho mỗi khách hàng.

Đếm số lượt xuất hiện của mối giá trị này và lập bảng.

Công thức số trung bình cộng:

\(\overline X  = \dfrac{{{x_1}{n_1} + {x_2}{n_2} + ... + {x_k}{n_k}}}{N}\)

Mốt của dấu hiệu là giá trị có tần số lớn nhất trong bảng tần số.

c) Vẽ biểu đồ.

Lời giải chi tiết:

Trong đợt bán “giải cứu dưa hấu”, một cửa hàng thống kê số quả dưa hấu bán cho 20 khách hàng đầu tiên như sau:

a) Dấu hiệu cần tìm hiểu ở đây là gì?

Dấu hiệu cần tìm hiểu ở đây là: Số quả dưa hấu bán cho mỗi khách hàng.

b) Lập bảng “tần số”, tìm trung bình cộng và mốt của dấu hiệu.

Bảng tần số:

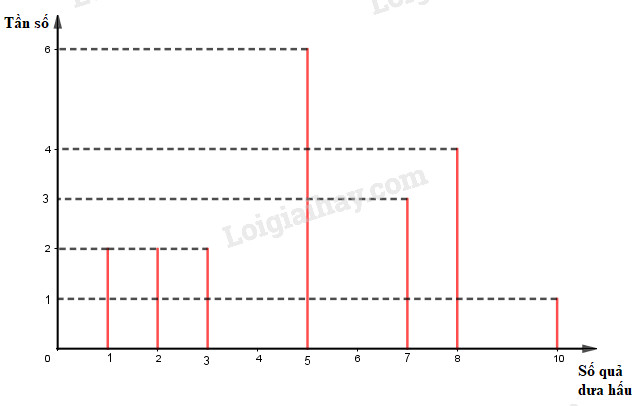
Số trung bình cộng: 

\(\dfrac{{1.2 + 2.2 + 3.2 + 5.6 + 7.3 + 8.4 + 10.1}}{{20}}\) \( = 5,25\)

Mốt của dấu hiệu là: \({M_0} = 5\) (giá trị có tần số lớn nhất)

c) Vẽ biểu đồ đoạn thẳng. (Trục hoành biểu diễn số quả dưa hấu của một người mua, trục tung biểu diễn tần số)

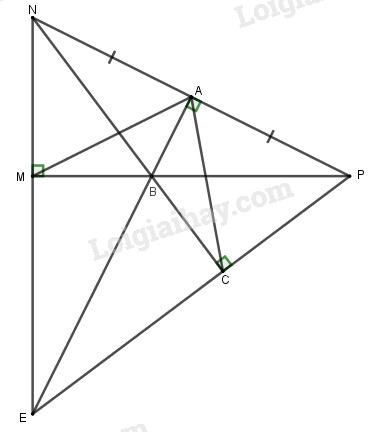
LG bài 2

Phương pháp giải:

a) Thu gọn đơn thức \(D\) và nhận xét. 

b) Thay giá trị của \(x,y\) (tmđk) vào đơn thức và tính giá trị.

Lời giải chi tiết:

Cho đơn thức \(D = 5{x^4}y.\left( { - \dfrac{3}{{10}}x{y^2}} \right)\)

a) Thu gọn, xác định hệ số và bậc của đơn thức \(D\).

\(\begin{array}{l}D = 5{x^4}y.\left( { - \dfrac{3}{{10}}x{y^2}} \right)\\ = 5.\left( { - \dfrac{3}{{10}}} \right).\left( {{x^4}.x} \right).\left( {y.{y^2}} \right)\\ =  - \dfrac{3}{2}{x^5}{y^3}\end{array}\)

Hệ số của D là \( - \dfrac{3}{2}\)

Bậc của D là \(5 + 3 = 8\). 

b) Tính giá trị của đơn thức \(D\) biết \(x =  - 1;y = \dfrac{1}{3}\).

Thay \(x =  - 1;y = \dfrac{1}{3}\) vào D ta được:

\(\begin{array}{l}D =  - \dfrac{3}{2}.{\left( { - 1} \right)^5}.{\left( {\dfrac{1}{3}} \right)^3}\\ =  - \dfrac{3}{2}.\left( { - 1} \right).\dfrac{1}{{27}} = \dfrac{1}{{18}}\end{array}\)

LG bài 3

Phương pháp giải:

a) Nhóm các đơn thức đồng dạng lại và thực hiện cộng, trừ các đơn thức đồng dạng trong \(M\left( x \right),N\left( x \right)\). 

b) Thực hiện cộng các đơn thức đồng dạng có trong \(M\left( x \right)\) và \(N\left( x \right)\) với nhau.

c) Thực hiện trừ các đơn thức đồng dạng có trong \(M\left( x \right)\) và \(N\left( x \right)\) cho nhau.

Nghiệm của đa thức \(Q\left( x \right)\) là giá trị của \(x\) làm cho \(Q\left( x \right) = 0\).

Lời giải chi tiết:

Cho hai đa thức \(M\left( x \right) = 2{x^4} + 2{x^3}\) \( - 5x - 10 + 3{x^2} + 2{x^3}\)

\(N\left( x \right) = 4{x^4} - 7 + 4{x^3} - 2{x^4} - 5x + 9\)

a) Thu gọn đa thức \(M\left( x \right);N\left( x \right)\) và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm dần của biến.

\(M\left( x \right) = 2{x^4} + 2{x^3}\) \( - 5x - 10 + 3{x^2} + 2{x^3}\)

\( = 2{x^4} + \left( {2{x^3} + 2{x^3}} \right) + 3{x^2} - 5x - 10\)

\( = 2{x^4} + 4{x^3} + 3{x^2} - 5x - 10\)

\(N\left( x \right) = 4{x^4} - 7\) \( + 4{x^3} - 2{x^4} - 5x + 9\)

\(\begin{array}{l} = \left( {4{x^4} - 2{x^4}} \right) + 4{x^3} - 5x + \left( {9 - 7} \right)\\ = 2{x^4} + 4{x^3} - 5x + 2\end{array}\)

Vậy \(M\left( x \right) = 2{x^4} + 4{x^3} + 3{x^2} - 5x - 10\)

\(N\left( x \right) = 2{x^4} + 4{x^3} - 5x + 2\)

b) Tính \(M\left( x \right) + N\left( x \right)\).

Ta có:

\(\begin{array}{l}M\left( x \right) + N\left( x \right)\\ = 2{x^4} + 4{x^3} + 3{x^2} - 5x - 10\\ + 2{x^4} + 4{x^3} - 5x + 2\\ = \left( {2{x^4} + 2{x^4}} \right) + \left( {4{x^3} + 4{x^3}} \right)\\ + 3{x^2} - \left( {5x + 5x} \right) - \left( {10 - 2} \right)\\ = 4{x^4} + 8{x^3} + 3{x^2} - 10x - 8\end{array}\)

c) Tính \(Q\left( x \right) = M\left( x \right) - N\left( x \right)\) và tìm nghiệm của đa thức \(Q\left( x \right)\).

\(\begin{array}{l}Q\left( x \right) = M\left( x \right) - N\left( x \right)\\ = 2{x^4} + 4{x^3} + 3{x^2} - 5x - 10\\ - \left( {2{x^4} + 4{x^3} - 5x + 2} \right)\\ = 2{x^4} + 4{x^3} + 3{x^2} - 5x - 10\\ - 2{x^4} - 4{x^3} + 5x - 2\\ = \left( {2{x^4} - 2{x^4}} \right) + \left( {4{x^3} - 4{x^3}} \right)\\ + 3{x^2} - \left( {5x - 5x} \right) - \left( {10 + 2} \right)\\ = 0{x^4} + 0{x^3} + 3{x^2} - 0x - 12\\ = 3{x^2} - 12\end{array}\)

\( \Rightarrow Q\left( x \right) = 3{x^2} - 12\)

Ta có: 

\(\begin{array}{l}Q\left( x \right) = 0\\ \Leftrightarrow 3{x^2} - 12 = 0\\ \Leftrightarrow 3{x^2} = 12\\ \Leftrightarrow {x^2} = 4\\ \Leftrightarrow x =  \pm 2\end{array}\)

Vậy \(2\) và \( - 2\) là các nghiệm của thì \(Q\left( x \right)\).

LG bài 4

Phương pháp giải:

a) Chứng minh \(\Delta BAN = \Delta BAP\) the trương hợp hai cạnh góc vuông.

Từ đó suy ra \(BN = BP\) dẫn đến \(\Delta BNP\) cân.

Sử dụng định lí: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn để so sánh BM và BN, từ đó suy ra BM và BP.

b) Chứng minh \(\Delta MBN = \Delta CBP\) theo trường hợp cạnh huyền – góc nhọn.

c) Chứng minh MA=CA bằng cách xét hai tam giác MNA và CPA 

Từ đó, xét hai tam giác MAB và CAB bằng nhau suy ra hai cặp góc tương ứng bằng nhau.

d) Nối M với E, chứng minh tam giác ENP đều suy ra \(\widehat {MNP} = {60^0}\).

Lời giải chi tiết:

Cho tam giác MNP vuông tại M có \(MN < MP\), \(A\) là trung điểm của \(NP\). Đường trung trực của đoạn thẳng \(NP\) cắt cạnh \(MP\) tại \(B\).

a) Chứng minh tam giác BNP cân, từ đó so sánh BM và BP.

A là trung điểm của NP thì \(AN = AP\) và BA là đường trung trực của NP

\( \Rightarrow BA \bot NP\)

\( \Rightarrow \widehat {BAN} = \widehat {BAP} = {90^0}\)

Xét \(\Delta BAN\) và \(\Delta BAP\) có:

\(\begin{array}{l}\widehat {BAN} = \widehat {BAP} = {90^0}\\BA\,\,\,chung\\AN = AP\end{array}\)

\( \Rightarrow \Delta BAN = \Delta BAP\) (hai cạnh góc vuông)

\( \Rightarrow BN = BP\) (cạnh tương ứng)

Tam giác BNP có BN=BP nên là tam giác cân tại B (đpcm).

Xét tam giác BMN có \(\widehat {BMN} = {90^0}\) nên \(\widehat {MNB} < \widehat {BMN}\) \( \Rightarrow BM < BN\)

Mà \(BN = BP\) nên \(BM < BP\).

b) Qua P kẻ đường vuông góc với đường thẳng NB tại điểm C. Chứng minh tam giác MBN bằng tam giác CBP.

Ta có: \(PC \bot AC \Rightarrow \widehat {PCB} = {90^0}\)

Xét \(\Delta MBN\) và \(\Delta CBP\) có:

\(\begin{array}{l}\widehat {NMB} = \widehat {PCB} = {90^0}\\BN = BP\,\left( {cmt} \right)\end{array}\)

\(\widehat {NBM} = \widehat {PBC}\) (đối đỉnh)

\( \Rightarrow \Delta MBN = \Delta CBP\) (cạnh huyền – góc nhọn) (đpcm)

c) Chứng minh AB là tia phân giác của góc MAC.

Từ câu b, \(\Delta MBN = \Delta CBP\)\( \Rightarrow MN = CP\) (cạnh tương ứng)

Xét \(\Delta MNP\) và \(\Delta CPN\) có:

\(\begin{array}{l}\widehat {NMP} = \widehat {PCN} = {90^0}\\NP\,\,\,chung\\MN = CP\,\,\left( {cmt} \right)\end{array}\)

\( \Rightarrow \Delta MNP = \Delta CPN\) (cạnh huyền – cạnh góc vuông)

\( \Rightarrow \widehat {MNP} = \widehat {CPN}\) (góc tương ứng) \( \Rightarrow \widehat {MNA} = \widehat {CPA}\)

Xét \(\Delta MNA\) và \(\Delta CPA\) có:

\(\begin{array}{l}MN = CP\left( {cmt} \right)\\\widehat {MNA} = \widehat {CPA}\left( {cmt} \right)\\NA = PA\left( {gt} \right)\\ \Rightarrow \Delta MNA = \Delta CPA\left( {c - g - c} \right)\end{array}\)

\( \Rightarrow MA = CA\) (cạnh tương ứng)

Lại có, \(\Delta MBN = \Delta CBP\) \( \Rightarrow MB = CB\) (cạnh tương ứng)

Xét \(\Delta MAB\) và \(\Delta CAB\) có:

\(\begin{array}{l}MA = CA\left( {cmt} \right)\\AB\,\,\,chung\\MB = CB\left( {cmt} \right)\\ \Rightarrow \Delta MBA = \Delta CBA\left( {c - g - c} \right)\end{array}\)

\( \Rightarrow \widehat {MAB} = \widehat {CAB}\) (góc tương ứng)

Vậy \(AB\) là tia phân giác của góc \(\widehat {MAC}\).

d) Gọi E là giao điểm của AB và tia PC. Tam giác MNP cần có thêm điều kiện gì để tam giác EBP cân tại B?

Nối M với E.

Tam giác NPE có hai đường cao NC và EA cắt nhau tại B nên B là trực tâm của tam giác.

Do đó \(PB \bot NE\).

Mà \(PB \bot MN\) nên M, N, E thẳng hàng (tiên đề Ơclit).

Tam giác EBP cân tại B thì BP=BE.

Xét \(\Delta BCP\) và \(\Delta BCE\) có:

\(\begin{array}{l}BC\,\,\,chung\\\widehat {BCP} = \widehat {BCE} = {90^0}\\BP = BE\left( {cmt} \right)\\ \Rightarrow \Delta BCP = \Delta BCE\left( {c - g - c} \right)\end{array}\)

\( \Rightarrow CP = CE\) (hai cạnh tương ứng)

Xét \(\Delta NCP\) và \(\Delta NCE\) có:

\(\begin{array}{l}CP = CE\left( {cmt} \right)\\\widehat {NCP} = \widehat {NCE} = {90^0}\\NC\,chung\\ \Rightarrow \Delta NCP = \Delta NCE\left( {c - g - c} \right)\end{array}\)

\( \Rightarrow NP = EP\) (cạnh tương ứng) (1)

Xét \(\Delta EAN\) và \(\Delta EAP\) có:

\(\begin{array}{l}AN = AP\\\widehat {EAN} = \widehat {EAP} = {90^0}\\EA\,\,chung\\ \Rightarrow \Delta EAN = \Delta EAP\left( {c - g - c} \right)\end{array}\)

\( \Rightarrow EN = EP\) (cạnh tương ứng) (2)

Từ (1) và (2) suy ra \(EN = EP = NP\)

\( \Rightarrow \Delta NEP\) đều \( \Rightarrow \widehat {ENP} = {60^0} \Rightarrow \widehat {MNP} = {60^0}\).

Vậy tam giác MNP có thêm điều kiện \(\widehat {MNP} = {60^0}\) thì tam giác EBP là tam giác cân.

HẾT

Loigiaihay.com