Đề thi học kì 2 môn toán lớp 6 năm 2019 - 2020 trường THCS Quang Trung

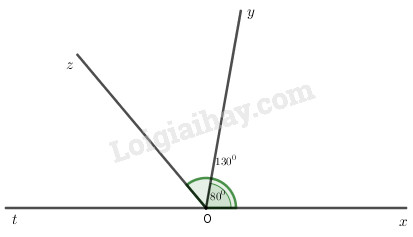
Đề bài

Câu 1 (3 điểm):

Thực hiện các phép tính:

a) \(\dfrac{1}{3} + \dfrac{5}{2} - \dfrac{{11}}{{12}}\)

b) \(\dfrac{{ - 7}}{{25}}.\dfrac{{11}}{{13}} + \dfrac{{ - 7}}{{25}}.\dfrac{2}{{13}} - \dfrac{{18}}{{25}}\)

c) \(\dfrac{{ - 5}}{9} + \dfrac{5}{9}:\left( {1\dfrac{2}{3} - 2\dfrac{1}{{12}}} \right)\)

Câu 2 (2,5 điểm):

Tìm \(x\), biết

a) \(x + \dfrac{3}{{10}} = \dfrac{{ - 4}}{{15}}\)

b) \(\left( {2,5x - 27} \right):\dfrac{4}{5} = 60\)

c) \(\left| {\dfrac{3}{4} - x} \right| + \dfrac{1}{6} = 1\dfrac{1}{6}\)

Câu 3 (1,5 điểm):

Cuối học kì I, khối 6 của một trường có \(540\) học sinh gồm ba loại: giỏi, khá, trung bình. Trong đó, số học sinh trung bình chiếm \(\dfrac{5}{{18}}\) số học sinh cả khối.

a) Tính tổng số học sinh khá và giỏi.

b) Cuối năm có \(34\) học sinh trung bình chuyển thành khá, nên số học sinh khá bằng \(\dfrac{5}{3}\) số học sinh giỏi. Tính số học sinh giỏi, số học sinh khá của khối 6 cuối năm?

Câu 4 (1 điểm):

Một chiếc xe đạp giá \(1\,\,700\,\,000\) đồng, nay hạ giá \(15\% \). Hỏi giá chiếc xe đạp bây giờ là bao nhiêu?

Câu 5 (2 điểm):

Trên cùng một nửa mặt phẳng bờ chứa tia \(Ox\), vẽ hai tia \(Oy\) và \(Oz\) sao cho \(\widehat {xOy} = {80^0}\) và \(\widehat {xOz} = {130^0}\).

a) Tính số đo góc \(\widehat {yOz}\).

b) Vẽ tia \(Ot\) là tia đối của tia \(Ox\). Chứng minh \(Oz\) là tia phân giác của \(\widehat {yOt}\) .

HẾT

LG câu 1

Phương pháp giải:

a) Quy đồng mẫu các phân số rồi thực hiện cộng trừ các phân số cùng mẫu

b) Sử dụng tính chất \(a.b + a.c = a\left( {b + c} \right)\)

c) Tính theo thứ tự trong ngoặc trước, sau đó là nhân chia, rồi đến cộng trừ 

Lời giải chi tiết:

a) \(\dfrac{1}{3} + \dfrac{5}{2} - \dfrac{{11}}{{12}}\)

\( = \dfrac{4}{{12}} + \dfrac{{30}}{{12}} - \dfrac{{11}}{{12}}\)

\( = \dfrac{{4 + 30 - 11}}{{12}}\)

\( = \dfrac{{23}}{{12}}\)

 b) \(\dfrac{{ - 7}}{{25}}.\dfrac{{11}}{{13}} + \dfrac{{ - 7}}{{25}}.\dfrac{2}{{13}} - \dfrac{{18}}{{25}}\)

\( = \dfrac{{ - 7}}{{25}}.\left( {\dfrac{{11}}{{13}} + \dfrac{2}{{13}}} \right) - \dfrac{{18}}{{25}}\)

\(\begin{array}{l} = \dfrac{{ - 7}}{{25}}.\dfrac{{13}}{{13}} - \dfrac{{18}}{{25}}\\ = \dfrac{{ - 7}}{{25}} + \dfrac{{ - 18}}{{25}}\\ = \dfrac{{ - 7 + \left( { - 18} \right)}}{{25}}\\ = \dfrac{{ - 25}}{{25}} =  - 1\end{array}\)

c) \(\dfrac{{ - 5}}{9} + \dfrac{5}{9}:\left( {1\dfrac{2}{3} - 2\dfrac{1}{{12}}} \right)\)

\(\begin{array}{l} = \dfrac{{ - 5}}{9} + \dfrac{5}{9}:\left( {\dfrac{5}{3} - \dfrac{{25}}{{12}}} \right)\\ = \dfrac{{ - 5}}{9} + \dfrac{5}{9}:\left( {\dfrac{{20}}{{12}} - \dfrac{{25}}{{12}}} \right)\\ = \dfrac{{ - 5}}{9} + \dfrac{5}{9}:\left( {\dfrac{{ - 5}}{{12}}} \right)\\ = \dfrac{{ - 5}}{9} + \dfrac{5}{9}.\dfrac{{ - 12}}{5}\\ = \dfrac{{ - 5}}{9} + \dfrac{{ - 12}}{9}\\ = \dfrac{{ - 17}}{9}\end{array}\)

LG câu 2

Phương pháp giải:

a) Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết

b) Muốn tìm số bị chia ta lấy thương nhân với số chia

Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ

Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết

c) Chuyển vế đưa về dạng \(\left| A \right| = m\left( {m \ge 0} \right)\)

TH1: \(A = m\)

TH2: \(A =  - m\) 

Lời giải chi tiết:

a) \(x + \dfrac{3}{{10}} = \dfrac{{ - 4}}{{15}}\)

\(\begin{array}{l}x = \dfrac{{ - 4}}{{15}} - \dfrac{3}{{10}}\\x = \dfrac{{ - 8}}{{30}} - \dfrac{9}{{30}}\\x = \dfrac{{ - 8 - 9}}{{30}}\\x = \dfrac{{ - 17}}{{30}}\end{array}\)

b) \(\left( {2,5x - 27} \right):\dfrac{4}{5} = 60\)

\(\begin{array}{l}2,5x - 27 = 60.\dfrac{4}{5}\\2,5x - 27 = 48\\2,5x = 27 + 48\\2,5x = 75\\x = 75:2,5\\x = 30\end{array}\)

c) \(\left| {\dfrac{3}{4} - x} \right| + \dfrac{1}{6} = 1\dfrac{1}{6}\)

\(\begin{array}{l}\left| {\dfrac{3}{4} - x} \right| = 1\dfrac{1}{6} - \dfrac{1}{6}\\\left| {\dfrac{3}{4} - x} \right| = 1\end{array}\)

TH1: \(\dfrac{3}{4} - x = 1\)

\(\begin{array}{l}x = \dfrac{3}{4} - 1\\x = \dfrac{3}{4} - \dfrac{4}{4}\\x = \dfrac{{ - 1}}{4}\end{array}\)

TH2: \(\dfrac{3}{4} - x =  - 1\)

\(\begin{array}{l}x = \dfrac{3}{4} - \left( { - 1} \right)\\x = \dfrac{3}{4} + 1\\x = \dfrac{3}{4} + \dfrac{4}{4}\\x = \dfrac{7}{4}\end{array}\)

LG câu 3

Phương pháp giải:

a) Muốn tìm tỉ số \(\dfrac{m}{n}\) của số \(a\) cho trước, ta lấy \(\dfrac{m}{n}.a\)

b) Tính tổng số học sinh khá và giỏi cuối năm của khổi 6 

Tính tỉ số số học sinh khá so với tổng số học sinh khá và giỏi

Tính số học sinh khá

Tính số học sinh giỏi

Lời giải chi tiết:

Cuối học kì I, khối 6 của một trường có \(540\) học sinh gồm ba loại: giỏi, khá, trung bình. Trong đó, số học sinh trung bình chiếm \(\dfrac{5}{{18}}\) số học sinh cả khối.

a) Tính tổng số học sinh khá và giỏi.

Số học sinh trung bình của khối 6 là: \(\dfrac{5}{{18}}.540 = 150\) học sinh

Tổng số học sinh khá và giỏi của khối 6 là: \(540 - 150 = 390\) học sinh

b) Cuối năm có \(34\) học sinh trung bình chuyển thành khá, nên số học sinh khá bằng \(\dfrac{5}{3}\) số học sinh giỏi. Tính số học sinh giỏi, số học sinh khá của khối 6 cuối năm?

Tổng số học sinh khá và giỏi cuối năm của khổi 6 là: \(390 + 34 = 424\) học sinh

Vì số học sinh khá bằng \(\dfrac{5}{3}\) số học sinh giỏi nên số học sinh khá bằng \(\dfrac{5}{{3 + 5}} = \dfrac{5}{8}\) tổng số học sinh khá và giỏi 

Vậy số học sinh khá của khối 6 cuối năm là: \(\dfrac{5}{8}.424 = 265\) học sinh

Số học sinh giỏi cuối năm là: \(424 - 265 = 159\) học sinh.

LG câu 4

Phương pháp giải:

- Tính số tiền được giảm giá.

- Tính giá còn lại cho chiếc xe.

Lời giải chi tiết:

Một chiếc xe đạp giá \(1\,\,700\,\,000\) đồng, nay hạ giá \(15\% \). Hỏi giá chiếc xe đạp bây giờ là bao nhiêu?

Số tiền được giảm giá cho chiếc xe là: 

\(15\% .1\,\,700\,\,000 = 255\,\,000\) (đồng)

Giá chiếc xe đạp bây giờ là:

\(1\,\,700\,\,000 - 255\,\,000 = 1\,445\,000\) (đồng)

Vậy giá chiếc xe còn là: \(1\,\,445\,\,000\) đồng.

LG câu 5

Phương pháp giải:

a) Chứng minh tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\). 

Sau đó sử dụng công thức cộng góc để suy ra \(\widehat {yOz}\).

b) Chứng minh tia \(Oz\) nằm giữa hai tia \(Oy\) và \(Ot\).

So sánh hai góc \(\widehat {tOz}\) và \(\widehat {zOy}\) rồi kết luận.

Lời giải chi tiết:

Trên cùng một nửa mặt phẳng bờ chứa tia \(Ox\), vẽ hai tia \(Oy\) và \(Oz\) sao cho \(\widehat {xOy} = {80^0}\) và \(\widehat {xOz} = {130^0}\).

a) Tính số đo góc \(\widehat {yOz}\).

Trên cùng một nửa mặt phẳng bờ chứa tia \(Ox\) ta có: \(\widehat {xOy} < \widehat {xOz}\left( {{{80}^0} < {{130}^0}} \right)\)

Do đó tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\)

\(\begin{array}{l} \Rightarrow \widehat {xOy} + \widehat {yOz} = \widehat {xOz}\\ \Rightarrow {80^0} + \widehat {yOz} = {130^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\widehat {yOz} = {130^0} - {80^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {50^0}\end{array}\)

Vậy \(\widehat {yOz} = {50^0}\).

b) Vẽ tia \(Ot\) là tia đối của tia \(Ox\). Chứng minh \(Oz\) là tia phân giác của \(\widehat {yOt}\) .

Tia \(Oz\) là tia đối của tia \(Ox\) nên \(\widehat {xOz}\) và \(\widehat {zOt}\) là hai góc kề bù

\( \Rightarrow \widehat {xOz} + \widehat {zOt} = {180^0}\) (tính chất hai góc kề bù)

\(\begin{array}{l} \Rightarrow {130^0} + \widehat {zOt} = {180^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\widehat {zOt} = {180^0} - {130^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {50^0}\end{array}\)

Vậy \(\widehat {zOt} = {50^0}\).

Trên cùng một nửa mặt phẳng bờ chứa tia \(Ox\) có \(\widehat {xOy} < \widehat {xOt}\left( {{{80}^0} < {{180}^0}} \right)\) nên tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Ot\)

\(\begin{array}{l} \Rightarrow \widehat {xOy} + \widehat {yOt} = \widehat {xOt}\\\,\,\,\,\,\,\,\,{80^0} + \widehat {yOt} = {180^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\widehat {yOt} = {180^0} - {80^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {100^0}\end{array}\)

Trên cùng một nửa mặt phẳng bờ chứa tia \(Ot\) có \(\widehat {tOz} < \widehat {tOy}\left( {{{50}^0} < {{100}^0}} \right)\) nên tia \(Oz\) nằm giữa hai tia \(Oy\) và \(Ot\). 

Mà \(\widehat {tOz} = \widehat {zOy} = {50^0}\) nên tia \(Oz\) là tia phân giác của góc \(\widehat {yOt}\).

HẾT

Loigiaihay.com