Đề thi học kì 2 môn toán lớp 6 năm 2019 - 2020 trường THCS Phan Chu Trinh

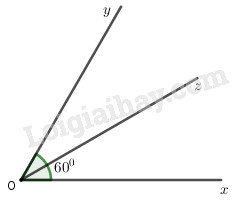
Đề bài

Bài 1  (2,0 điểm):

Thực hiện phép tính

a) \(\dfrac{1}{5} - \dfrac{9}{{10}} + \dfrac{4}{5}\)

b) \(\dfrac{1}{4} - \dfrac{5}{7}.\dfrac{7}{{20}}\)

c) \(\dfrac{5}{9} + \dfrac{4}{9}:4\)

d) \(\dfrac{{ - 5}}{8}.\dfrac{{11}}{{28}} - \dfrac{{11}}{{28}}.\dfrac{3}{8}\)

Bài 2 (2,0 điểm):

Tìm \(x\) biết

a) \(x + \dfrac{5}{6} = \dfrac{1}{2}\)

b) \(x - \dfrac{4}{9} = \dfrac{{ - 1}}{3}\)

c) \(\dfrac{7}{8} - x =  - \dfrac{1}{4}\)

d) \(\dfrac{7}{{12}} - \dfrac{x}{4} = \dfrac{1}{{12}}\)

Bài 3 (2,0 điểm):

Nguyên liệu để muối dưa cải gồm rau cải, hành tươi, đường và muối. Khối lượng hành, đường và muối theo thứ tự bằng 5%, \(\dfrac{1}{{1000}}\) và \(\dfrac{3}{{40}}\) khối lượng rau cải. Vậy nếu muối 5kg rau cải thì cần bao nhiêu gam hành, đường và muối.

Bài 4 (3 điểm):

a)  Vẽ góc \(\widehat {xOy} = {60^0}\) và vẽ tia phân giác của góc đó

b) Trên cùng một nửa mặt phẳng bờ chứa tia Oa, vẽ hai tia Ob, Oc sao cho \(\widehat {aOb} = {60^0},\widehat {aOc} = {90^0}.\) Tính số đo góc \(\widehat {bOc}\).

Bài 5 (1 điểm):

Cho \(M = 1\dfrac{1}{8}.1\dfrac{1}{{15}}.1\dfrac{1}{{24}}\)\(.1\dfrac{1}{{35}}.1\dfrac{1}{{48}}.1\dfrac{1}{{63}}\)

\(N = \dfrac{1}{{15}} + \dfrac{2}{{45}} + \dfrac{3}{{135}}\) \( + \dfrac{4}{{345}} + \dfrac{5}{{759}} + \dfrac{6}{{1485}}\)

Tính tỉ số \(\dfrac{M}{N}.\)

HẾT

LG bài 1

Phương pháp giải:

a) Sử dụng tính chất giao hoán, kết hợp: \(a + b = b + a;\) \(\left( {a + b} \right) + c = \left( {a + c} \right) + b\) 

b) Thực hiện theo thứ tự nhân trước, trừ sau

c) Thực hiện theo thứ tự chia trước, cộng sau

d) Sử dụng tính chất phân phối: \(ab - ac = a\left( {b - c} \right)\)

Lời giải chi tiết:

a) \(\dfrac{1}{5} - \dfrac{9}{{10}} + \dfrac{4}{5}\)

\(\begin{array}{l} = \left( {\dfrac{1}{5} + \dfrac{4}{5}} \right) - \dfrac{9}{{10}}\\ = \dfrac{5}{5} - \dfrac{9}{{10}}\\ = \dfrac{{10}}{{10}} - \dfrac{9}{{10}}\\ = \dfrac{1}{{10}}\end{array}\)

b) \(\dfrac{1}{4} - \dfrac{5}{7}.\dfrac{7}{{20}}\)

\(\begin{array}{l} = \dfrac{1}{4} - \dfrac{{5.7}}{{7.20}}\\ = \dfrac{1}{4} - \dfrac{5}{{20}}\\ = \dfrac{1}{4} - \dfrac{1}{4}\\ = 0\end{array}\)

c) \(\dfrac{5}{9} + \dfrac{4}{9}:4\)

\(\begin{array}{l} = \dfrac{5}{9} + \dfrac{4}{9}.\dfrac{1}{4}\\ = \dfrac{5}{9} + \dfrac{1}{9}\\ = \dfrac{6}{9}\\ = \dfrac{2}{3}\end{array}\) 

d) \(\dfrac{{ - 5}}{8}.\dfrac{{11}}{{28}} - \dfrac{{11}}{{28}}.\dfrac{3}{8}\)

\(\begin{array}{l} = \dfrac{{11}}{{28}}\left( {\dfrac{{ - 5}}{8} - \dfrac{3}{8}} \right)\\ = \dfrac{{11}}{{28}}\left( {\dfrac{{ - 5 - 3}}{8}} \right)\\ = \dfrac{{11}}{{28}}.\dfrac{{ - 8}}{8}\\ = \dfrac{{11}}{{28}}.\left( { - 1} \right)\\ = \dfrac{{ - 11}}{{28}}\end{array}\)

LG bài 2

Phương pháp giải:

a) Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết

b) Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ

c) Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu

d) Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu 

Lời giải chi tiết:

a) \(x + \dfrac{5}{6} = \dfrac{1}{2}\) 

\(\begin{array}{l}x = \dfrac{1}{2} - \dfrac{5}{6}\\x = \dfrac{3}{6} - \dfrac{5}{6}\\x = \dfrac{{3 - 5}}{6}\\x = \dfrac{{ - 2}}{6}\\x = \dfrac{{ - 1}}{3}\end{array}\)

b) \(x - \dfrac{4}{9} = \dfrac{{ - 1}}{3}\)

\(\begin{array}{l}x = \dfrac{{ - 1}}{3} + \dfrac{4}{9}\\x = \dfrac{{ - 3}}{9} + \dfrac{4}{9}\\x = \dfrac{{ - 3 + 4}}{9}\\x = \dfrac{1}{9}\end{array}\)

c) \(\dfrac{7}{8} - x =  - \dfrac{1}{4}\)

\(\begin{array}{l}x = \dfrac{7}{8} - \left( { - \dfrac{1}{4}} \right)\\x = \dfrac{7}{8} + \dfrac{1}{4}\\x = \dfrac{7}{8} + \dfrac{2}{8}\\x = \dfrac{{7 + 2}}{8}\\x = \dfrac{9}{8}\end{array}\)

d) \(\dfrac{7}{{12}} - \dfrac{x}{4} = \dfrac{1}{{12}}\)

\(\begin{array}{l}\dfrac{x}{4} = \dfrac{7}{{12}} - \dfrac{1}{{12}}\\\dfrac{x}{4} = \dfrac{6}{{12}}\\\dfrac{x}{4} = \dfrac{1}{2}\\2.x = 4\\x = 4:2\\x = 2\end{array}\)

LG bài 3

Phương pháp giải:

Muốn tìm tỉ số \(\dfrac{m}{n}\) của một số \(a\) cho trước, ta lấy \(\dfrac{m}{n}.a\)

Muốn tìm \(m\% \) của một số  \(a\) cho trước, ta lấy \(\dfrac{{m.a}}{{100}}\) 

Lời giải chi tiết:

Nguyên liệu để muối dưa cải gồm rau cải, hành tươi, đường và muối. Khối lượng hành, đường và muối theo thứ tự bằng 5%, \(\dfrac{1}{{1000}}\) và \(\dfrac{3}{{40}}\) khối lượng rau cải. Vậy nếu muối 5kg rau cải thì cần bao nhiêu gam hành, đường và muối.

Đổi 5kg=5000g

Khối lượng hành cần dùng để muối 5kg rau cải là:

\(5000.5\% \) \( = 5000.\dfrac{5}{{100}} = 250g\)

Khối lượng đường cần dùng để muối 5kg rau cải là:

\(5000.\dfrac{1}{{1000}} = 5g\)

Khối lượng muối cần dùng để muối 5kg rau cải là:

\(5000.\dfrac{3}{{40}} = \dfrac{{5000.3}}{{40}} = 375g\)

Đáp số: 

250 gam hành

5 gam đường

375 gam muối

LG bài 4

Phương pháp giải:

a) Dùng thước đo góc vẽ góc \({60^0}\).

Sử dụng tính chất tia phân giác tính góc tạo thành và dựng hình.

b) Chứng minh tia \(Ob\) nằm giữa hai tia \(Oa\) và \(Oc\).

Sau đó sử dụng công thức cộng góc.

Lời giải chi tiết:

a) Vẽ góc \(\widehat {xOy} = {60^0}\) và vẽ tia phân giác của góc đó.

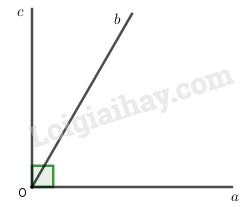
b) Trên cùng một nửa mặt phẳng bờ chứa tia Oa, vẽ hai tia Ob, Oc sao cho \(\widehat {aOb} = {60^0},\widehat {aOc} = {90^0}.\) Tính số đo góc \(\widehat {bOc}\).

Trên cùng một nửa mặt phẳng bờ chứa tia \(Oa\) ta có:

\(\widehat {aOb} < \widehat {aOc}\left( {{{60}^0} < {{90}^0}} \right)\) nên tia \(Ob\) nằm giữa hai tia \(Oa\) và \(Oc\)

Ta có:

\(\begin{array}{l}\widehat {aOb} + \widehat {bOc} = \widehat {aOc}\\{60^0} + \widehat {bOc} = {90^0}\\\,\,\,\,\,\,\,\,\,\,\,\widehat {bOc} = {90^0} - {60^0}\\\,\,\,\,\,\,\,\,\,\,\,\widehat {bOc} = {30^0}\end{array}\)

Vậy \(\widehat {bOc} = {30^0}\).

LG bài 5

Phương pháp giải:

Rút gọn, tính giá trị \(M,N\) suy ra tỉ số \(\dfrac{M}{N}\)

Chú ý sử dụng: \(\dfrac{n}{{a\left( {a + n} \right)}} = \dfrac{1}{a} - \dfrac{1}{{a + n}}\)

Lời giải chi tiết:

\(\begin{array}{l}M = 1\dfrac{1}{8}.1\dfrac{1}{{15}}.1\dfrac{1}{{24}}.1\dfrac{1}{{35}}.1\dfrac{1}{{48}}.1\dfrac{1}{{63}}\\ = \dfrac{9}{8}.\dfrac{{16}}{{15}}.\dfrac{{25}}{{24}}.\dfrac{{36}}{{35}}.\dfrac{{49}}{{48}}.\dfrac{{64}}{{63}}\\ = \dfrac{{3.3.4.4.5.5.6.6.7.7.8.8}}{{2.4.3.5.4.6.5.7.6.8.7.9}}\\ = \dfrac{{\left( {3.4.5.6.7.8} \right).\left( {3.4.5.6.7.8} \right)}}{{\left( {2.3.4.5.6.7} \right).\left( {4.5.6.7.8.9} \right)}}\\ = \dfrac{{8.3}}{{2.9}} = \dfrac{4}{3}\\N = \dfrac{1}{{15}} + \dfrac{2}{{45}} + \dfrac{3}{{135}} + \dfrac{4}{{345}} + \dfrac{5}{{759}} + \dfrac{6}{{1485}}\\2N = 2\left( {\dfrac{1}{{15}} + \dfrac{2}{{45}} + \dfrac{3}{{135}} + \dfrac{4}{{345}} + \dfrac{5}{{759}} + \dfrac{6}{{1485}}} \right)\\ = \dfrac{2}{{15}} + \dfrac{4}{{45}} + \dfrac{6}{{135}} + \dfrac{8}{{345}} + \dfrac{{10}}{{759}} + \dfrac{{12}}{{1485}}\\ = \dfrac{2}{{3.5}} + \dfrac{4}{{5.9}} + \dfrac{6}{{9.15}} + \dfrac{8}{{15.23}} + \dfrac{{10}}{{23.33}} + \dfrac{{12}}{{33.45}}\\ = \dfrac{1}{3} - \dfrac{1}{5} + \dfrac{1}{5} - \dfrac{1}{9} \\+ \dfrac{1}{9} - \dfrac{1}{{15}} + \dfrac{1}{{15}} - \dfrac{1}{{23}} + \dfrac{1}{{23}} - \dfrac{1}{{33}} + \dfrac{1}{{33}} - \dfrac{1}{{45}}\\ = \dfrac{1}{3} - \dfrac{1}{{45}}\\ = \dfrac{{15 - 1}}{{45}} = \dfrac{{14}}{{45}}\end{array}\)

Vậy \(\dfrac{M}{N} = \dfrac{4}{3}:\dfrac{{14}}{{45}} = \dfrac{4}{3}.\dfrac{{45}}{{14}} = \dfrac{{30}}{7}\).

HẾT

Loigiaihay.com