Đề thi giữa học kì 1 Vật lí 11 Kết nối tri thức - Đề số 8Đề thi giữa học kì 1 - Đề số 8Đề bài
PHẦN I. CÂU TRẮC NGHIỆM PHƯƠNG ÁN NHIỀU LỰA CHỌN.
Câu 1 :
Theo định nghĩa. Dao động điều hòa là
Câu 2 :
Chọn phát biểu đúng nhất? Hình chiếu của một chuyển động tròn đều lên một đường kính
Câu 3 :
Vật dao động điều hòa theo trục Ox. Phát biểu nào sau đây đúng?
Câu 4 :
Trong dao động điều hòa, đại lượng nào sau đây không có giá trị âm?
Câu 5 :
Đồ thị li độ theo thời gian của dao động điều hòa là một
Câu 6 :
Dao động là chuyển động có
Câu 7 :
Dao động điều hòa có thể được coi như hình chiếu của một chuyển động tròn đều xuống một
Câu 8 :
Một vật dao động điều hòa với theo phương trình x = Acos(ωt + φ) với A, ω, φ là hằng số thì pha của dao động
Câu 9 :
Phương trình dao động điều hòa của một chất điểm có dạng x = Acos(ωt + φ). Độ dài quỹ đạo của dao động là
Câu 10 :
Một vật nhỏ dao động điều hòa theo phương trình x = Acos10t (t tính bằng s). Tại t = 2 s, pha của dao động là
Câu 11 :
Đại lượng nào dưới đây đặc trưng cho độ lệch về thời gian giữa hai dao động điều hòa cùng chu kì?
Câu 12 :
Biên độ của hệ dao động điều hòa phụ thuộc yếu tố nào?
Câu 13 :
Pha của dao động được dùng để xác định
Câu 14 :
Chu kì dao động là
Câu 15 :
Một vật dao động điều hòa, mỗi chu kỳ dao động vật đi qua VTCB
Câu 16 :
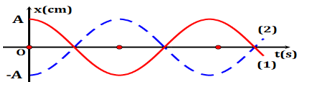
Đồ thi biễu diễn hai dao động điều hòa cùng phương, cùng tần số, cùng biên độ A như hình vẽ. Hai dao động này luôn
Câu 17 :
Một chất điểm dao động điều hoà có chu kì T = 2 s. Tần số góc ω của dao động là
Câu 18 :
Một chất điểm dao động điều hoà có tần số góc ω = 20π (rad/s). Tần số củadao động là
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI.
a) Biên độ dao động của vật bằng 0,2 cm.
Đúng
Sai
b) Chu kì dao động của vật bằng 0,4 s
Đúng
Sai
c) Pha ban đầu của dao động là 0,5π rad.
Đúng
Sai
d) Tại thời điểm t = 0,5 s vật ở vị trí biên.
Đúng
Sai
Câu 2 :
Một vật dao động điều hòa dọc theo trục Ox. Khi qua vị trí cân bằng, tốc độ của vật là 8π cm/s. Khi ở biên, gia tốc của vật có độ lớn là 16π2 cm/s2. Tại t = 0, vật qua vị trí có li độ x = 2 cm theo chiều dương. a) Tần số góc của vật là \(\frac{1}{{2\pi }}\) rad/s.
Đúng
Sai
b) Vật dao động điều hòa với biên độ là 4 cm.
Đúng
Sai
c) Pha ban đầu của vật dao động điều hòa là -\(\frac{\pi }{3}\) rad.
Đúng
Sai
d) Phương trình dao động của vật là: \(x = 4\cos (2\pi t + \frac{\pi }{3})\)(cm).
Đúng
Sai
Câu 3 :
Một con lắc lò xo gồm vật nhỏ có khối lượng m và lò xo có độ cứng 40N/m đang dao động điều hoà với biên độ 5cm a) Trong quá trình vật dao động cơ năng của vật được bảo toàn
Đúng
Sai
b) Cơ năng của vật có giá trị là 0,032 J khi vật qua vị trí có li độ là 3 cm
Đúng
Sai
c) Động năng của vật có giá trị là 0,032 J khi vật qua vị trí có li độ 3 cm.
Đúng
Sai
d) Nếu giữ nguyên khối lượng của vật và thay đổi lò xo có độ cứng tăng lên 2 lần mà vẫn giữ cho vật do động có biên độ 5 cm thì cơ năng của vật tăng lên 2 lần so với ban đầu.
Đúng
Sai
Câu 4 :
Máy đo địa chấn được sử dụng để phát hiện và đo đạc những rung động địa chấn được tạo ra bởi sự dịch chuyển của lớp vỏ Trái Đất. Tần số của những cơn địa chấn thường nằm trong khoảng 30 Hz – 40 Hz. Năng lượng từ các cơn địa chấn có khả năng kích thích con lắc lò xo bên trong máy đo làm đầu bút di chuyển để vẽ lên giấy như hình vẽ.
a) Dao động của con lắc lò xo trong máy địa chấn là dao động duy trì.
Đúng
Sai
b) Đầu bút di chuyển và vẽ được lên tờ giấy là do các cơn địa chấn tạo ra dao động duy trì.
Đúng
Sai
c) Tần số dao động của những con lắc lò xo trong máy địa chấn vào khoảng 30 Hz – 40 Hz.
Đúng
Sai
d) Để máy địa chấn ghi nhận được kết quả tốt nhất thì tần số riêng của con lắc lò xo phải có giá trị thật nhỏ so với con số 30 Hz – 40 Hz.
Đúng
Sai
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN.
Lời giải và đáp án
PHẦN I. CÂU TRẮC NGHIỆM PHƯƠNG ÁN NHIỀU LỰA CHỌN.
Câu 1 :
Theo định nghĩa. Dao động điều hòa là
Đáp án : D Phương pháp giải :
Vận dụng kiến thức về định nghĩa dao động điều hòa Lời giải chi tiết :
Dao động điều hòa là một dạng dao động mà li độ của vật có phương trình dạng x=Acos(ωt+φ) hoặc x=Asin(ωt+φ), trong đó A là biên độ, ω là tần số góc và φ là pha ban đầu. Phương trình này thể hiện chuyển động có dạng sin hoặc cosin theo thời gian. Đáp án: D
Câu 2 :
Chọn phát biểu đúng nhất? Hình chiếu của một chuyển động tròn đều lên một đường kính
Đáp án : A Phương pháp giải :
Vận dụng kiến thức về mối liên hệ giữa dao động điều hòa và chuyển động tròn đều. Lời giải chi tiết :
Hình chiếu của một chuyển động tròn đều lên một đường kính là một dao động điều hòa vì khi chuyển động tròn đều, hình chiếu của vật lên một đường kính sẽ dao động qua lại quanh một vị trí cân bằng với li độ có dạng sin hoặc cosin. Đáp án: A
Câu 3 :
Vật dao động điều hòa theo trục Ox. Phát biểu nào sau đây đúng?
Đáp án : A Phương pháp giải :
Vận dụng kiến thức về quỹ đạo của vật dao động điều hòa Lời giải chi tiết :
Trong dao động điều hòa theo trục Ox, vật chuyển động qua lại trên một đoạn thẳng quanh vị trí cân bằng O. Lực kéo về biến thiên theo li độ của vật nên không phải là một hằng số. Li độ thay đổi theo thời gian dạng sin hoặc cosin, không tỉ lệ trực tiếp với thời gian. Đáp án: A
Câu 4 :
Trong dao động điều hòa, đại lượng nào sau đây không có giá trị âm?
Đáp án : D Phương pháp giải :
Vận dụng kiến thức về tính chất của các đại lượng trong dao động điều hòa Lời giải chi tiết :
Biên độ là giá trị cực đại của li độ và là một đại lượng dương hoặc bằng 0. Li độ, pha và pha ban đầu có thể nhận giá trị âm tùy theo vị trí của vật hoặc giá trị của góc pha. Đáp án: D
Câu 5 :
Đồ thị li độ theo thời gian của dao động điều hòa là một
Đáp án : C Phương pháp giải :
Vận dụng kiến thức về dạng đồ thị của dao động điều hòa Lời giải chi tiết :
Đồ thị li độ x theo thời gian t là một đường hình sin hoặc cosin Đáp án: C
Câu 6 :
Dao động là chuyển động có
Đáp án : A Phương pháp giải :
Vận dụng kiến thức về đặc điểm của dao động. Lời giải chi tiết :
Dao động là chuyển động qua lại quanh vị trí cân bằng trong không gian giới hạn. Do đó, đáp án phù hợp là chọn phát biểu chính xác nhất theo đặc điểm dao động. Đáp án: A
Câu 7 :
Dao động điều hòa có thể được coi như hình chiếu của một chuyển động tròn đều xuống một
Đáp án : D Phương pháp giải :
Vận dụng kiến thức về quan hệ giữa dao động điều hòa và chuyển động tròn đều Lời giải chi tiết :
Dao động điều hòa có thể được biểu diễn là hình chiếu của một chuyển động tròn đều lên một đường thẳng nằm trong mặt phẳng quỹ đạo. Hình chiếu của điểm quay tròn sẽ dao động qua lại quanh vị trí cân bằng trên đường thẳng đó. Đáp án: D
Câu 8 :
Một vật dao động điều hòa với theo phương trình x = Acos(ωt + φ) với A, ω, φ là hằng số thì pha của dao động
Đáp án : C Phương pháp giải :
Vận dụng kiến thức về hương trình dao động điều hòa Lời giải chi tiết :
Một vật dao động điều hòa với theo phương trình x = Acos(ωt + φ) với A, ω, φ là hằng số thì pha của dao động là hàm bậc nhất với thời gian Đáp án: C
Câu 9 :
Phương trình dao động điều hòa của một chất điểm có dạng x = Acos(ωt + φ). Độ dài quỹ đạo của dao động là
Đáp án : B Phương pháp giải :
Vận dụng kiến thức về độ dài quỹ đạo dao động điều hòa Lời giải chi tiết :
Quỹ đạo của dao động điều hòa là đoạn thẳng giữa hai điểm cực đại. Độ dài quỹ đạo bằng 2A Đáp án: B
Câu 10 :
Một vật nhỏ dao động điều hòa theo phương trình x = Acos10t (t tính bằng s). Tại t = 2 s, pha của dao động là
Đáp án : C Phương pháp giải :
Vận dụng kiến thức về pha dao động tại thời điểm t Lời giải chi tiết :
Pha dao động tại thời điểm t = 2 s là 10t = 10.2 = 20 rad Đáp án: C
Câu 11 :
Đại lượng nào dưới đây đặc trưng cho độ lệch về thời gian giữa hai dao động điều hòa cùng chu kì?
Đáp án : D Phương pháp giải :
Vận dụng kiến thức về cách đo độ lệch giữa hai dao động điều hòa cùng chu kỳ. Lời giải chi tiết :
Độ lệch về thời gian giữa hai dao động điều hòa cùng chu kỳ được xác định thông qua độ lệch pha, vì pha cho biết vị trí và thời điểm của dao động. Đáp án: D
Câu 12 :
Biên độ của hệ dao động điều hòa phụ thuộc yếu tố nào?
Đáp án : A Phương pháp giải :
Vận dụng kiến thức về các yếu tố ảnh hưởng đến biên độ của dao động điều hòa Lời giải chi tiết :
Biên độ dao động phụ thuộc vào cách kích thích ban đầu, vì đây là yếu tố quyết định mức độ dao động ban đầu của vật. Đáp án: A
Câu 13 :
Pha của dao động được dùng để xác định
Đáp án : C Phương pháp giải :
Vận dụng kiến thức về khái niệm pha của dao động và mục đích của nó trong mô tả dao động điều hòa. Lời giải chi tiết :
Pha của dao động xác định trạng thái của dao động tại một thời điểm cụ thể, bao gồm cả vị trí và hướng chuyển động của vật tại thời điểm đó. Đáp án: C
Câu 14 :
Chu kì dao động là
Đáp án : D Phương pháp giải :
Vận dụng kiến thức về định nghĩa của chu kỳ trong dao động điều hòa. Lời giải chi tiết :
Chu kỳ là khoảng thời gian ngắn nhất để vật trở lại trạng thái dao động ban đầu, bao gồm cả vị trí và hướng chuyển động. Đáp án: D
Câu 15 :
Một vật dao động điều hòa, mỗi chu kỳ dao động vật đi qua VTCB
Đáp án : D Phương pháp giải :
Vận dụng kiến thức về quá trình dao động của vật qua vị trí cân bằng trong một chu kỳ. Lời giải chi tiết :
Trong mỗi chu kỳ, vật dao động điều hòa sẽ đi qua vị trí cân bằng hai lần: một lần theo chiều dương và một lần theo chiều âm. Đáp án: D
Câu 16 :
Đồ thi biễu diễn hai dao động điều hòa cùng phương, cùng tần số, cùng biên độ A như hình vẽ. Hai dao động này luôn
Đáp án : A Phương pháp giải :
Vận dụng kiến thức về tính chất của hai dao động điều hòa cùng phương, cùng tần số, cùng biên độ và độ lệch pha giữa chúng. Lời giải chi tiết :
Vì hai dao động có cùng tần số và biên độ, nhưng lệch pha nhau π rad, nên chúng luôn có li độ đối nhau tại mọi thời điểm. Đáp án: A
Câu 17 :
Một chất điểm dao động điều hoà có chu kì T = 2 s. Tần số góc ω của dao động là
Đáp án : A Phương pháp giải :
Vận dụng kiến thức về tần số góc của dao động Lời giải chi tiết :
\(\omega = \frac{{2\pi }}{2} = \pi \,{\rm{rad/s}}\) Đáp án: A
Câu 18 :
Một chất điểm dao động điều hoà có tần số góc ω = 20π (rad/s). Tần số củadao động là
Đáp án : B Phương pháp giải :
Vận dụng kiến thức về tần số của dao động. Lời giải chi tiết :
\(f = \frac{{20\pi }}{{2\pi }} = 10\,{\rm{Hz}}\) Đáp án: B
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI.
a) Biên độ dao động của vật bằng 0,2 cm.
Đúng
Sai
b) Chu kì dao động của vật bằng 0,4 s
Đúng
Sai
c) Pha ban đầu của dao động là 0,5π rad.
Đúng
Sai
d) Tại thời điểm t = 0,5 s vật ở vị trí biên.
Đúng
Sai
Đáp án
a) Biên độ dao động của vật bằng 0,2 cm.
Đúng
Sai
b) Chu kì dao động của vật bằng 0,4 s
Đúng
Sai
c) Pha ban đầu của dao động là 0,5π rad.
Đúng
Sai
d) Tại thời điểm t = 0,5 s vật ở vị trí biên.
Đúng
Sai
Phương pháp giải :
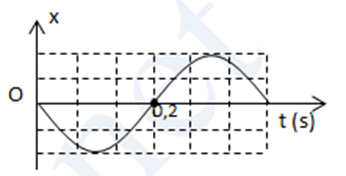
Vận dụng kiến thức về đọc đồ thị Lời giải chi tiết :
a) Đúng. Nhìn vào đồ thị, ta thấy biên độ dao động (li độ lớn nhất) của vật là 0,2 cm. b) Đúng. Chu kỳ là khoảng thời gian ngắn nhất để vật lặp lại trạng thái dao động cũ. Quan sát đồ thị, ta thấy một chu kỳ dao động là từ t = 0 s đến t = 0,4 s. c) Đúng. Dựa vào đồ thị, tại thời điểm t = 0, li độ của vật đang là 0 và đi theo chiều âm, điều này cho thấy pha ban đầu có thể là −0,5π hoặc 0,5π rad (tuỳ cách quy ước chiều). d) Sai. Dựa vào đồ thị, tại thời điểm t = 0,5 s, vật đang ở vị trí cân bằng, không phải ở vị trí biên.
Câu 2 :
Một vật dao động điều hòa dọc theo trục Ox. Khi qua vị trí cân bằng, tốc độ của vật là 8π cm/s. Khi ở biên, gia tốc của vật có độ lớn là 16π2 cm/s2. Tại t = 0, vật qua vị trí có li độ x = 2 cm theo chiều dương. a) Tần số góc của vật là \(\frac{1}{{2\pi }}\) rad/s.
Đúng
Sai
b) Vật dao động điều hòa với biên độ là 4 cm.
Đúng
Sai
c) Pha ban đầu của vật dao động điều hòa là -\(\frac{\pi }{3}\) rad.
Đúng
Sai
d) Phương trình dao động của vật là: \(x = 4\cos (2\pi t + \frac{\pi }{3})\)(cm).
Đúng
Sai
Đáp án
a) Tần số góc của vật là \(\frac{1}{{2\pi }}\) rad/s.
Đúng
Sai
b) Vật dao động điều hòa với biên độ là 4 cm.
Đúng
Sai
c) Pha ban đầu của vật dao động điều hòa là -\(\frac{\pi }{3}\) rad.
Đúng
Sai
d) Phương trình dao động của vật là: \(x = 4\cos (2\pi t + \frac{\pi }{3})\)(cm).
Đúng
Sai
Phương pháp giải :
Vận dụng kiến thức về phương trình li độ Lời giải chi tiết :
a) Sai. Tần số góc của vật là \(\omega = \frac{{16{\pi ^2}}}{{8\pi }} = 2\pi (rad/s)\) rad/s. b) Đúng. Vật dao động điều hòa với biên độ là \(A = \frac{{8\pi }}{{2\pi }} = 4\) cm. c) Đúng. Tại t = 0, vật có li độ x = 2 cm và A = 4 cm, Pha ban đầu của vật dao động điều hòa là -\(\frac{\pi }{3}\) rad. d) Đúng. Phương trình dao động của vật là: \(x = 4\cos (2\pi t + \frac{\pi }{3})\)(cm).
Câu 3 :
Một con lắc lò xo gồm vật nhỏ có khối lượng m và lò xo có độ cứng 40N/m đang dao động điều hoà với biên độ 5cm a) Trong quá trình vật dao động cơ năng của vật được bảo toàn
Đúng
Sai
b) Cơ năng của vật có giá trị là 0,032 J khi vật qua vị trí có li độ là 3 cm
Đúng
Sai
c) Động năng của vật có giá trị là 0,032 J khi vật qua vị trí có li độ 3 cm.
Đúng
Sai
d) Nếu giữ nguyên khối lượng của vật và thay đổi lò xo có độ cứng tăng lên 2 lần mà vẫn giữ cho vật do động có biên độ 5 cm thì cơ năng của vật tăng lên 2 lần so với ban đầu.
Đúng
Sai
Đáp án
a) Trong quá trình vật dao động cơ năng của vật được bảo toàn
Đúng
Sai
b) Cơ năng của vật có giá trị là 0,032 J khi vật qua vị trí có li độ là 3 cm
Đúng
Sai
c) Động năng của vật có giá trị là 0,032 J khi vật qua vị trí có li độ 3 cm.
Đúng
Sai
d) Nếu giữ nguyên khối lượng của vật và thay đổi lò xo có độ cứng tăng lên 2 lần mà vẫn giữ cho vật do động có biên độ 5 cm thì cơ năng của vật tăng lên 2 lần so với ban đầu.
Đúng
Sai
Phương pháp giải :
Vận dụng kiến thức về con lắc lò xo Lời giải chi tiết :
a) Đúng. Trong dao động điều hòa (không có ma sát), cơ năng của vật dao động luôn được bảo toàn. b) Sai. Cơ năng được tính là \(W = \frac{1}{2}k{A^2} = 0,05J\) c) Đúng. Tổng cơ năng E = 0,05 J, khi li độ là x = 0,03 m, động năng Wđ = W −Wt = 0,032 J. d) Đúng. Khi độ cứng tăng lên 2 lần, cơ năng cũng tăng lên 2 lần
Câu 4 :
Máy đo địa chấn được sử dụng để phát hiện và đo đạc những rung động địa chấn được tạo ra bởi sự dịch chuyển của lớp vỏ Trái Đất. Tần số của những cơn địa chấn thường nằm trong khoảng 30 Hz – 40 Hz. Năng lượng từ các cơn địa chấn có khả năng kích thích con lắc lò xo bên trong máy đo làm đầu bút di chuyển để vẽ lên giấy như hình vẽ.
a) Dao động của con lắc lò xo trong máy địa chấn là dao động duy trì.
Đúng
Sai
b) Đầu bút di chuyển và vẽ được lên tờ giấy là do các cơn địa chấn tạo ra dao động duy trì.
Đúng
Sai
c) Tần số dao động của những con lắc lò xo trong máy địa chấn vào khoảng 30 Hz – 40 Hz.
Đúng
Sai
d) Để máy địa chấn ghi nhận được kết quả tốt nhất thì tần số riêng của con lắc lò xo phải có giá trị thật nhỏ so với con số 30 Hz – 40 Hz.
Đúng
Sai
Đáp án
a) Dao động của con lắc lò xo trong máy địa chấn là dao động duy trì.
Đúng
Sai
b) Đầu bút di chuyển và vẽ được lên tờ giấy là do các cơn địa chấn tạo ra dao động duy trì.
Đúng
Sai
c) Tần số dao động của những con lắc lò xo trong máy địa chấn vào khoảng 30 Hz – 40 Hz.
Đúng
Sai
d) Để máy địa chấn ghi nhận được kết quả tốt nhất thì tần số riêng của con lắc lò xo phải có giá trị thật nhỏ so với con số 30 Hz – 40 Hz.
Đúng
Sai
Phương pháp giải :
Vận dụng kiến thức về dao động duy trì Lời giải chi tiết :
a) Đúng. Dao động của con lắc lò xo trong máy đo địa chấn được duy trì bởi năng lượng từ các cơn địa chấn. b) Đúng. Dao động duy trì của con lắc được tạo ra nhờ năng lượng từ các cơn địa chấn. c) Đúng. Tần số dao động của con lắc phải nằm trong khoảng này để đo chính xác các cơn địa chấn. d) Sai. Tần số riêng của con lắc nên gần bằng tần số của các cơn địa chấn để có thể cộng hưởng và ghi nhận kết quả tốt nhất.
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN.
Phương pháp giải :
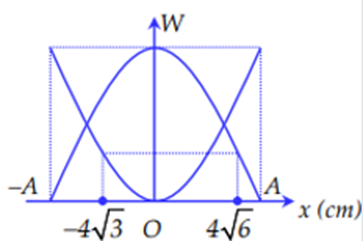
+ Đọc đồ thị W-x + Sử dụng biểu thức tính cơ năng: \(W = {W_t} + {W_d}\) Lời giải chi tiết :
Từ đồ thị ta có: Thế năng của vật: \({W_{t1}} = \frac{1}{2}kx_1^2 = \frac{1}{2}.50.{(0,04\sqrt 6 )^2} = 0,24J\) Động năng của vật: \({W_{d1}}\) + Tại vị trí: \({x_2} = - 4\sqrt 3 cm\) Thế năng của vật: \({W_{t2}} = \frac{1}{2}kv_2^2 = \frac{1}{2}.50.{( - 0,04\sqrt 3 )^2} = 0,12J\) Động năng của vật: \({W_{d2}}\) Và từ đồ thị, ta có: \({W_{{d_1}}} = {W_{{t_2}}}\) Ta suy ra: \(\begin{array}{l}\left\{ \begin{array}{l}{W_{t1}} = 0,24J\\{W_{d1}} = 0,12J\end{array} \right.\\ \Rightarrow W = {W_{{t_1}}} + {W_{{d_1}}} = 0,24 + 0,12 = 0,36J\end{array}\) Đáp án: 0,36 Phương pháp giải :
Vận dụng kiến thức về hiện tượng cộng hưởng Lời giải chi tiết :
+ Chiều dài của mỗi bước chân: L=50cm + Tần số dao động riêng của nước trong xô: \({f_0} = \frac{1}{{{T_0}}} = 1Hz\) + Nước trong xô sóng sánh mạnh nhất khi nhịp bước của người có tần số trùng với tần số dao động riêng của nước trong xô. Vậy người đó bước đều với tần số: \(f = {f_0} = 1Hz \Rightarrow T = \frac{1}{f} = 1s\) Nước trong xô sóng sánh mạnh nhất khi người đi với vận tốc: \({\rm{\;}}v = \frac{s}{t} = \frac{L}{T} = \frac{{50}}{1} = 50\left( {cm/s} \right)\) Đáp án: 50 Phương pháp giải :
Vận dụng kiến thức về đọc đồ thị Lời giải chi tiết :
0,5T = 0,2 => T = 0,4 s Đáp án: 0,4 Phương pháp giải :
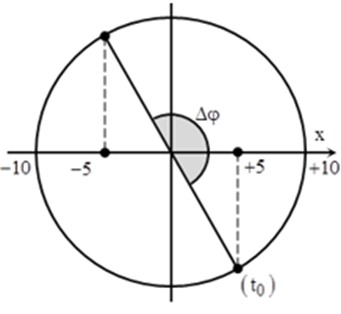
Vận dụng kiến thức về dao động điều hòa Lời giải chi tiết :
Chu kì dao động của chất điểm T = 0,4 s. + Ta có Δt = 10T + 0,5T = 4,2 s. Trong mỗi chu kì có 1 lần vật đi qua vị trí x = – 5 cm theo chiều dương. → Trong 10T sẽ có 10 lần vật đi qua vị trí x = – 5 cm theo chiều dương. Nửa chu kì còn lại vật đến vị trí x = – 5 cm theo chiềm âm. → Vậy kể từ thời điểm ban đầu, có 10 lần vật đi qua vị trí x = – 5 cm theo chiều dương. Đáp án: 10 Phương pháp giải :
Vận dụng kiến thức về cơ năng Lời giải chi tiết :
Quãng đường vật đi được trong một chu kì là: \({S_T} = 4{\rm{A}} \Rightarrow A = 5cm\) Đáp án: 0,1 Phương pháp giải :
Vận dụng kiến thức về dao động điều hòa Lời giải chi tiết :
Một chất điểm chuyển động tròn đều trên đường tròn bán kính R với tốc độ góc ω thì hình chiếu của nó trên một trục nằm trong mặt phẳng quỹ đạo sẽ dao động điều hòa với biên độ đúng bằng R và tần số góc đúng bằng ω Hình chiếu của chất điểm lên trục Ox nằm trong mặt phẳng quỹ đạo dao động điều hòa với biên độ A = 10 cm và tần số góc ω = 5 rad/s => tốc độ cực đại là \({v_{\max }} = \omega A = 50cm/s\) Đáp án: 50
|

























Danh sách bình luận