Giải đề thi học kì 2 toán lớp 10 năm 2020 - 2021 trường THPT Trần Quang KhảiLàm bàiQuảng cáo
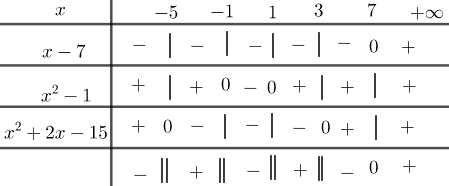
Câu hỏi 1 : (2 điểm) Giải các bất phương trình sau : a) \(\dfrac{2}{{2{x^2} - 2}} > \dfrac{1}{{{x^2} + 2x - 15}}\) b) \(|x - 4| + 7x - 12 < {x^2}\) Phương pháp giải: a) Tìm điều kiện của bất phương trình. Chuyển vế bất phương trình. Quy đồng và phân tích các biểu thức của tử và mẫu thành nhân tử. Sử dụng bảng xét dấu để tìm nghiệm. b) xét các trường hợp phá dấu giá trị tuyệt đối. Lời giải chi tiết: \(\dfrac{2}{{2{x^2} - 2}} > \dfrac{1}{{{x^2} + 2x - 15}}\left( 1 \right)\) Điều kiện: \(x \ne \pm 1;x \ne 3;x \ne - 5\) \(\begin{array}{l}\left( 1 \right) \Leftrightarrow \dfrac{1}{{{x^2} - 1}} - \dfrac{1}{{{x^2} + 2x - 15}} > 0\\ \Leftrightarrow \dfrac{{2x - 14}}{{\left( {{x^2} - 1} \right)\left( {{x^2} + 2x - 15} \right)}} > 0\\ \Leftrightarrow \dfrac{{x - 7}}{{\left( {{x^2} - 1} \right)\left( {{x^2} + 2x - 15} \right)}} > 0\end{array}\) Bảng xét dấu:
Từ bảng xét dấu ta được tập nghiệm của bất phương trình là: \(S = \left( { - 5; - 2} \right) \cup \left( {1;3} \right) \cup \left[ {7; + \infty } \right)\). b) \(\begin{array}{l}\left| {x - 4} \right| + 7x - 12 < {x^2}\left( 2 \right)\\ \Leftrightarrow \left| {x - 4} \right| < - 7x + 12 + {x^2}\\ \Leftrightarrow \left| {x - 4} \right| < \left( {x - 4} \right)\left( {x - 3} \right)\end{array}\) TH1: \(x \ge 4\)
\(\left( 2 \right) \Leftrightarrow x - 4 < \left( {x - 4} \right)\left( {x - 3} \right) \Leftrightarrow x \ne 4\) Vậy \(x > 4\) TH2: \(x < 4\) \(\begin{array}{l}\left( 2 \right) \Leftrightarrow 4 - x < \left( {x - 4} \right)\left( {x - 3} \right)\\ \Leftrightarrow \left( {x - 4} \right)\left( {x - 2} \right) > 0\\ \Leftrightarrow \left[ \begin{array}{l}x > 4\\x < 2\end{array} \right. \Leftrightarrow x < 2\end{array}\) Vậy \(S = \left( { - \infty ;2} \right) \cup \left( {4; + \infty } \right)\) Câu hỏi 2 : \((2\) điểm) Cho \(\tan x = - \dfrac{3}{4}\left( {\dfrac{\pi }{2} < x < \pi } \right)\). Tính \(\cos x,\cos 2x,\tan \left( {x - \dfrac{\pi }{4}} \right),\)\(\sin \left( {\dfrac{\pi }{3} + x} \right)\). Phương pháp giải: \(\dfrac{1}{{{{\cos }^2}x}} = {\tan ^2}x + 1\) \(\dfrac{\pi }{2} < x < \pi \) thì \(\cos x < 0,\sin x > 0\) \(\cos 2x = 2{\cos ^2}x - 1\) \(\tan \left( {a - b} \right) = \dfrac{{\tan a - \tan b}}{{1 + \tan a.\tan b}}\) \(\sin \left( {a + b} \right)\)\( = \sin a.\cos b + \cos a.\sin b\) Lời giải chi tiết: Ta có \(\dfrac{1}{{{{\cos }^2}x}} = {\tan ^2}x + 1 = \dfrac{{25}}{{16}}\) \( = > {\cos ^2}x = \dfrac{{16}}{{25}},{\sin ^2}x = \dfrac{9}{{25}}\) Do \(\dfrac{\pi }{2} < x < \pi \) nên \(\cos x < 0,\sin x > 0\) => \(\cos x = \dfrac{{ - 4}}{5},\sin x = \dfrac{3}{5}\) \(\begin{array}{l}\cos 2x = 2{\cos ^2}x - 1 = \dfrac{7}{{25}}\\\tan \left( {x - \dfrac{\pi }{4}} \right) = \dfrac{{\tan x - \tan \dfrac{\pi }{4}}}{{1 + \tan x.\tan \dfrac{\pi }{4}}}\\ = - 7\\\sin \left( {\dfrac{\pi }{3} + x} \right)\\ = \sin \dfrac{\pi }{3}.\cos x + \cos \dfrac{\pi }{3}.\sin x\\ = \dfrac{{\sqrt 3 }}{2}.\left( { - \dfrac{4}{5}} \right) + \dfrac{1}{2}.\dfrac{3}{5} = \dfrac{{3 - 4\sqrt 3 }}{{10}}\end{array}\) Câu hỏi 3 : (2 điểm) Chứng minh rằng: a) \(\dfrac{{\sin x}}{{1 + \cos x}} + \dfrac{{1 + \cos x}}{{\sin x}} = \dfrac{2}{{\sin x}}\) b) \(\dfrac{{{{\sin }^2}x \cdot (2\cos x + 3)}}{{2{{\cos }^2}\dfrac{x}{2} + \cos 2x - 3}} = - 1 - \cos x\) Phương pháp giải: a) - Quy đồng vế trái, biến đổi về vế phải - Sử dụng công thức \({\sin ^2}x + {\cos ^2}x = 1\) b) - Quy đồng vế trái, biến đổi về vế phải - Sử dụng các công thức: \(\begin{array}{l}2{\cos ^2}\dfrac{x}{2} - 1 = \cos x\\\cos 2x + 1 = 2{\cos ^2}x\\{\sin ^2}x = 1 - {\cos ^2}x\end{array}\) Lời giải chi tiết: a) \(\begin{array}{l}\dfrac{{\sin x}}{{1 + \cos x}} + \dfrac{{1 + \cos x}}{{\sin x}}\\ = \dfrac{{{{\sin }^2}x + {{\left( {\cos x + 1} \right)}^2}}}{{\sin x.\left( {1 + \cos x} \right)}}\\ = \dfrac{{2\cos x + 2}}{{\sin x\left( {1 + \cos x} \right)}} = \dfrac{2}{{\sin x}} = VP\end{array}\) b) \(\begin{array}{l}\dfrac{{{{\sin }^2}x\left( {2\cos x + 3} \right)}}{{2{{\cos }^2}\dfrac{x}{2} + \cos 2x - 3}}\\ = \dfrac{{{{\sin }^2}x\left( {2\cos x + 3} \right)}}{{\left( {2{{\cos }^2}\dfrac{x}{2} - 1} \right) + \left( {\cos 2x + 1} \right) - 2}}\\ = \dfrac{{{{\sin }^2}x\left( {2\cos x + 3} \right)}}{{\cos x + 2{{\cos }^2}x - 3}}\\ = \dfrac{{{{\sin }^2}x\left( {2\cos x + 3} \right)}}{{\left( {\cos x - 1} \right)\left( {2\cos x + 3} \right)}}\\ = \dfrac{{{{\sin }^2}x}}{{\cos x - 1}} = \dfrac{{\left( {1 - \cos x} \right)\left( {1 + \cos x} \right)}}{{\cos x - 1}}\\ = - 1 - \cos x = VP\end{array}\) Câu hỏi 4 : ( 1 điểm) Trong mặt phẳng Oxy, cho đường tròn \((C):{x^2} + {y^2} - 4x + 6y + 3 = 0\). Viết phương trình tiếp tuyến \(\Delta \) của đường tròn \((C)\) biết tiếp tuyến song song với đường thẳng \((d):3x - y + 1 = 0\). Phương pháp giải: Tìm tâm và bán kính của đường tròn. \(\Delta //d \Rightarrow \Delta \) có dạng: \(3x - y + c = 0\) Vì \(\Delta \) là tiếp tuyến của (C) nên \(d\left( {I,\Delta } \right) = R\) Lời giải chi tiết: \(\begin{array}{l}\left( C \right):{x^2} + {y^2} - 4x + 6y + 3 = 0\\ \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 10\end{array}\) => (C) có tâm \(I\left( {2; - 3} \right),R = \sqrt {10} \) \(\Delta //d \Rightarrow \Delta \) có dạng: \(3x - y + c = 0\)\(c \ne 1\) Vì \(\Delta \) là tiếp tuyến của (C) nên \(d\left( {I,\Delta } \right) = R \Leftrightarrow \dfrac{{\left| {3.2 - \left( { - 3} \right) + c} \right|}}{{\sqrt {10} }} = \sqrt {10} \) \(\begin{array}{l} \Leftrightarrow \dfrac{{\left| {c + 9} \right|}}{{\sqrt {10} }} = \sqrt {10} \\ \Leftrightarrow \left| {c + 9} \right| = 10\\ \Leftrightarrow \left[ \begin{array}{l}c = 1\\c = - 19\end{array} \right.\end{array}\) Vậy \(\Delta :3x - y - 19 = 0\) Câu hỏi 5 : ( 3 điểm) Trong mặt phẳng Oxy cho tam giác ABC với A(4;-3), B(2;1), C(-2;2). a) Viết phương trình tham số cạnh AC của tam giác ABC. b) Viết phương trình tổng quát đường cao AH của tam giác ABC. c) Viết phương trình đường tròn tâm B và đi qua điểm C. Phương pháp giải: a) Tìm vecto \(\overrightarrow {CA} \) Viết phương trình đường thẳng AC qua A và nhận \(\overrightarrow {CA} \) làm vtcp. b) + Tìm vecto \(\overrightarrow {BC} \) + Đường thẳng qua \(M\left( {{x_0};{y_0}} \right)\) và nhận \(\overrightarrow n \left( {a;b} \right)\) là vtpt có phương trình: \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\) c) Đường tròn tâm \(I\left( {{x_0};{y_0}} \right)\) và đi qua M có bán kính R=IM. Lời giải chi tiết:
a) \(\overrightarrow {CA} = \left( {6; - 5} \right)\) Đường thẳng AC qua A và nhận \(\overrightarrow {CA} = \left( {6; - 5} \right)\) làm vtcp có phương trình: \(\left\{ \begin{array}{l}x = 4 + 6t\\y = - 3 - 5t\end{array} \right.\left( {t \in \mathbb{R}} \right)\) b) \(\overrightarrow {BC} = \left( { - 4;1} \right)\) AH là đường thẳng qua A và vuông góc với BC nên nhận vecto \(\overrightarrow {BC} \) làm vtpt: \(\begin{array}{l} - 4\left( {x - 4} \right) + 1.\left( {y + 3} \right) = 0\\ \Leftrightarrow 4x - y - 19 = 0\end{array}\) c) Đường tròn đi qua C nên có bán kính \(R = BC = \sqrt {{{\left( { - 2 - 2} \right)}^2} + {{\left( {2 - 1} \right)}^2}} \)\( = \sqrt {17} \). Phương trình của đường tròn cần tìm là: \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 17\) Quảng cáo
|