Phương pháp giải:

Lời giải chi tiết:

\(H\left( {\frac{{14}}{5};\frac{{17}}{5}} \right)\).

Phương pháp giải:

Lời giải chi tiết:

\(6x + 5y + 37 = 0\)

Phương pháp giải:

Trọng tâm \(G\) của tam giác ABC:  \(\left\{ \matrix{  {x_G} = {{{x_A} + {x_B} + {x_C}} \over 3} \hfill \cr   {y_G} = {{{y_A} + {y_B} + {y_C}} \over 3} \hfill \cr}  \right.\)

Đường thẳng đi qua điểm \(M({x_0};{y_0})\) và có 1 VTCP \(\overrightarrow u (a;b)\) có phương trình tham số: \(\left\{ \matrix{  x = {x_0} + at \hfill \cr   y = {y_0} + bt \hfill \cr}  \right.\).

Lời giải chi tiết:

G là trọng tâm tam giác ABC \( \Rightarrow \left\{ \matrix{  {x_G} = {{{x_A} + {x_B} + {x_C}} \over 3} \hfill \cr   {y_G} = {{{y_A} + {y_B} + {y_C}} \over 3} \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {x_G} = {{ - 1 + 4 - 6} \over 3} \hfill \cr   {y_G} = {{3 + 7 + 5} \over 3} \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {x_G} =  - 1 \hfill \cr   {y_G} = 5 \hfill \cr}  \right. \Rightarrow G( - 1;5)\)

\( \Rightarrow \overrightarrow {AG}  = \left( {0;2} \right)\)

Phương trình tham số của đường thẳng AG là: \(\left\{ \matrix{  x =  - 1 \hfill \cr   y = 5 + 2t \hfill \cr}  \right.\)

Chọn: A

Phương pháp giải:

Lời giải chi tiết:

\(x + 1 = 0;\,\,y = 0;\,\,x + 3 = 0;\,\,y - 2 = 0\)

Phương pháp giải:

Lời giải chi tiết:

\(y + 1 = 0\) và \(4x + 3y + 3 = 0\).

Phương pháp giải:

Lời giải chi tiết:

\(A\left( {9; - 2} \right);\,\,B\left( { - 12;1} \right)\)

Phương pháp giải:

Lời giải chi tiết:

\(x - 2y + 6 = 0\)

Phương pháp giải:

Lời giải chi tiết:

Học sinh tự giải

Phương pháp giải:

Lời giải chi tiết:

\(M\left( {1;0} \right)\)

Phương pháp giải:

Lời giải chi tiết:

\(3x - 7y - 13 = 0\) và \(7x + 3y - 36 = 0\).

Phương pháp giải:

Lời giải chi tiết:

Học sinh tự giải

Phương pháp giải:

Viết phương trình đường thẳng EF.

Lời giải chi tiết:

Gọi phương trình đường thẳng EF là \(y = ax + b\) ta có :

\(\left\{ \begin{array}{l}E \in EF\\F \in EF\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3a + b =  - 2\\ - a + b =  - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{4}\\b =  - \dfrac{{11}}{4}\end{array} \right. \Leftrightarrow EF:\,\,y = \dfrac{1}{4}x - \dfrac{{11}}{4}\).

\(G \in Ox;\,\,G \in EF \Rightarrow \) tọa độ điểm G là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}y = 0\\y = \dfrac{1}{4}x - \dfrac{{11}}{4}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 0\\x = 11\end{array} \right. \Rightarrow G\left( {11;0} \right)\).

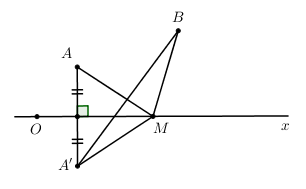
Chọn B.

Phương pháp giải:

+) Nhận xét A, B nằm cùng phía so với trục Ox.

+) Lấy A’ đối xứng với A qua Ox ta có: \(MA + MB = MA' + MB \ge A'B\). Dấu "=" xảy ra \( \Leftrightarrow M = Ox \cap A'B\).

Lời giải chi tiết:

A(1,2) và B(3,4) nằm cùng phía đối với trục Ox.

Gọi A’ đối xứng với A qua Ox \( \Rightarrow A'\left( {1; - 2} \right)\) và \(MA = MA'\).

Ta có : \(MA + MB = MA' + MB \ge A'B\). Dấu "=" xảy ra \( \Leftrightarrow M = Ox \cap A'B\).

Phương trình A’B là :

\(\dfrac{{x - 1}}{{3 - 1}} = \dfrac{{y + 2}}{{4 + 2}} \Leftrightarrow 3\left( {x - 1} \right) = y + 2 \Leftrightarrow 3x - y - 5 = 0\)

Cho \(y = 0 \Leftrightarrow x = \dfrac{5}{3} \Rightarrow M\left( {\dfrac{5}{3};0} \right)\)

\( \Rightarrow a = 5;\,\,b = 3 \Rightarrow S = 8\)

Chọn B.

Phương pháp giải:

+) Tìm điều kiện của \(m\) để hai đường thẳng đã cho cắt nhau.

+)  Gọi giao điểm của 2 đường thẳng là điểm \(A\left( {x;\;y} \right) \Rightarrow OA = \sqrt {{x^2} + {y^2}} \)

Lời giải chi tiết:

Hai đường thẳng \({d_1},\;{d_2}\) cắt nhau \( \Leftrightarrow \frac{m}{3} \ne \frac{3}{m} \Leftrightarrow m \ne  \pm 3.\)

Tọa độ giao điểm A của 2 đường thẳng là nghiệm của hệ :

\(\left\{ \begin{array}{l}mx + 3y - 3 = 0\\3x + my - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}mx + 3y - 3 = 0\\\left( {m - 3} \right)x = \left( {m - 3} \right)y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}mx + 3y - 3 = 0\\x = y\end{array} \right. \Leftrightarrow x = y = \frac{3}{{m + 3}}\)

\( \Rightarrow OA = \sqrt {{{\left( {\frac{3}{{m + 3}}} \right)}^2} + {{\left( {\frac{3}{{m + 3}}} \right)}^2}}  = \sqrt {2.\frac{9}{{{{\left( {m + 3} \right)}^2}}}}  = \frac{{3\sqrt 2 }}{{\left| {m + 3} \right|}}\)

Chọn B.

Phương pháp giải:

Đường thẳng \(y = ax + b\) song song với đường thẳng \(y = a'x + b'\) \( \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\) 

Lời giải chi tiết:

Đường thẳng \(y = ax + b\) song song với đường thẳng \(y = 2x + 13 \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b \ne 13\end{array} \right. \Rightarrow y = 2x + b.\)

 Lại có đường thẳng \(y = 2x + b\) đi qua điểm \(A\left( { - 1;\;3} \right) \Rightarrow 3 = 2.\left( { - 1} \right) + b \Leftrightarrow b = 3 + 2 = 5\;\;\left( {tm} \right).\)

\( \Rightarrow a = 2;\;b = 5.\)

Chọn C.

Phương pháp giải:

Tìm mối quan hệ giữa đường thẳng (AB) và đường thẳng (d) từ đó tính độ dài IA, IB để tính tỉ số.

Cho đường thẳng \(\Delta :ax + by + c = 0\) và điểm \({M_0}\left( {{x_0};{y_0}} \right) \Rightarrow {d_{\left( {{M_0};\Delta } \right)}} = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}.\) 

Lời giải chi tiết:

Ta có \(\overrightarrow {AB}  = \left( {4; - 2} \right) = 2\left( {2;\, - 1} \right)\); đường thẳng (d) có VTCP là \(\overrightarrow u  = \left( {1;2} \right) \Rightarrow \overrightarrow {AB}  \bot \overrightarrow u .\) 

\( \Rightarrow \) Đường thẳng (AB) vuông góc với đường thẳng (d)

Đường thẳng AB cắt d tại I \( \Rightarrow \) IA, IB lần lượt là khoảng cách từ A và B đến đường thẳng d

\( \Rightarrow IA = d\left( {A;\,\,d} \right) = \frac{{\left| { - 6 - 5 - 1} \right|}}{{\sqrt {4 + 1} }} = \frac{{12}}{{\sqrt 5 }}\,\,;\,\,IB = d\left( {B;\,d} \right) = \frac{{\left| {2 - 3 - 1} \right|}}{{\sqrt {4 + 1} }} = \frac{2}{{\sqrt 5 }} \Rightarrow \frac{{IA}}{{IB}} = 6.\) 

Chọn A.

Phương pháp giải:

Đường thẳng \(ax + by + c = 0\) song song với đường thẳng \(a'x + b'y + c' = 0 \Leftrightarrow \frac{a}{{a'}} = \frac{b}{{b'}} \ne \frac{c}{{c'}}.\)

Xác định VTPT và điểm đi qua của \(\Delta \) để viết phương trình đường thẳng \(\Delta \)

Lời giải chi tiết:

Viết phương trình đường thẳng \(\Delta \) qua \(A\left( {1; - 2} \right)\) và song song đường thẳng \(\left( d \right):2x - 3y + 2 = 0\)

Đường thẳng \(\left( d \right):2x - 3y + 2 = 0\) có VTPT \(\overrightarrow n  = \left( {2; - 3} \right)\)

Đường thẳng \(\Delta \) song song đường thẳng \(\left( d \right):2x - 3y + 2 = 0\) nên cũng nhận \(\overrightarrow n  = \left( {2; - 3} \right)\) làm VTPT

\(A\left( {1; - 2} \right) \in \left( \Delta  \right) \Rightarrow \) Phương trình  \(\left( \Delta  \right):2\left( {x - 1} \right) - 3\left( {y + 2} \right) = 0 \Leftrightarrow 2x - 3y - 8 = 0\)

Chọn A.

Phương pháp giải:

Góc giữa hai đường thẳng \(d,\;d'\)  có hai VTPT lần lượt là \(\overrightarrow a ,\;\overrightarrow b \) được tính bởi công thức: \(\cos \left( {d;d'} \right) = \frac{{\left| {\overrightarrow a .\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}.\)

Lời giải chi tiết:

Đường thẳng \(d:\sqrt 3 x + y = 0\) nhận \(\overrightarrow a  = \left( {\sqrt 3 ;\;1} \right)\) là 1 VTPT

Đường thẳng \(d':mx + y - 1 = 0\) nhận \(\overrightarrow b  = \left( {m;\;1} \right)\) là 1 VTPT

\(\begin{array}{l} \Rightarrow \cos \left( {d,d'} \right) = \left| {\cos \left( {\overrightarrow a ;\overrightarrow b } \right)} \right| = \frac{1}{2} \Leftrightarrow \frac{{\left| {\sqrt 3 .m + 1} \right|}}{{2.\sqrt {{m^2} + 1} }} = \frac{1}{2} \Leftrightarrow \left| {\sqrt 3 .m + 1} \right| = \sqrt {{m^2} + 1} \\ \Leftrightarrow 3{m^2} + 2\sqrt 3 m + 1 = {m^2} + 1 \Leftrightarrow 2{m^2} + 2\sqrt 3 m = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\\m =  - \sqrt 3 \end{array} \right..\end{array}\) 

Chọn D.

Phương pháp giải:

Gọi phương trình đường tròn có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) , thay tọa độ A, B, C vào để được hệ phương trình 3 ẩn a, b, c. Giải hệ phương trình để tìm 3 ẩn a, b, c rồi suy ra phương trình.

Lời giải chi tiết:

Gọi phương trình đường tròn có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\)

Vì \(A,\;B,\;C\) đều thuộc đường tròn nên có hệ:

\(\begin{array}{l}\left\{ \begin{array}{l}1 + 4 - 2a - 4b + c = 0\\25 + 4 - 10a - 4b + c = 0\\1 + 9 - 2a + 6b + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2a - 4b + c =  - 5\\ - 10a - 4b + c =  - 29\\ - 2x + 6b + c =  - 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b =  - \frac{1}{2}\\c =  - 1\end{array} \right.\\ \Rightarrow {x^2} + {y^2} - 6x + y - 1 = 0.\end{array}\)

Chọn C.

Phương pháp giải:

Thay tọa độ điểm M và phương trình đường thẳng d, gọi  M  theo t. Dựa vào dữ kiện còn lại viết phương trình tìm t.

Lời giải chi tiết:

Ta có : \(M \in \left( d \right) \Rightarrow \left\{ \begin{array}{l}a = 3 + t\\b = 2 + t\end{array} \right. \Rightarrow M\left( {3 + t;2 + t} \right)\)

Lại có : \(d\left( {M;\Delta } \right) = 2\sqrt 5  \Leftrightarrow \frac{{\left| {2.\left( {3 + t} \right) - \left( {2 + t} \right) - 3} \right|}}{{\sqrt {{2^2} + {1^2}} }} = 2\sqrt 5 \)

\(\begin{array}{l} \Leftrightarrow \left| {t + 1} \right| = 10 \Leftrightarrow \left[ \begin{array}{l}t = 9 \Rightarrow a = 12\,\,\,(tm)\\t =  - 11 \Rightarrow a =  - 8\,\,\,(ktm)\end{array} \right.\\ \Rightarrow b = 11 \Rightarrow a + b = 12 + 11 = 23.\end{array}\) 

Chọn B.

Phương pháp giải:

Tìm giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\). Thay tọa độ giao điểm đó vào \(\left( {{d_3}} \right)\) để tìm \(m\)

Lời giải chi tiết:

Gọi \(M\) là giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\)

\( \Rightarrow \) Tọa độ điểm \(M\) là nghiệm của hệ: \(\left\{ \begin{array}{l}3x - 4y + 7 = 0\\5x + y + 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 1\\y = 1\end{array} \right. \Rightarrow M\left( { - 1;1} \right)\)

Để 3 đường thẳng đồng quy \( \Leftrightarrow \) chúng đồng quy tại \(M \Leftrightarrow M \in \left( {{d_3}} \right)\)

\( \Leftrightarrow  - m + 1 - m + 3 = 0 \Leftrightarrow 2m = 4 \Leftrightarrow m = 2.\) 

Chọn A.

Phương pháp giải:

Gọi \(\overrightarrow {{n_1}}  = \left( {a;b} \right)\) là một VTPT của \(\left( d \right).\) Viết phương trình \(\left( d \right).\)

Góc giữa hai đường thẳng bằng góc giữa hai VTPT (VTCP)

Giải phương trình tìm tỉ số \(\frac{a}{b}\) từ đó suy ra phương trình của \(\left( d \right).\)

Lời giải chi tiết:

Gọi \(\overrightarrow {{n_1}}  = \left( {a;b} \right)\) là một VTPT của \(\left( d \right).\)

 Phương trình \(\left( d \right):\,\,a\left( {x - 1} \right) + b\left( {y - 1} \right) = 0 \Leftrightarrow ax + by - a - b = 0\)

Đường thẳng \(\Delta :x - 3y + 2 = 0\) có VTPT \(\overrightarrow {{n_2}}  = \left( {1; - 3} \right)\)

Ta có: \(\cos \left( {d;\Delta } \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right)} \right| \Leftrightarrow \cos {45^o} = \frac{{\left| {a - 3b} \right|}}{{\sqrt {{a^2} + {b^2}} .\sqrt {10} }}\)

\(\begin{array}{l} \Leftrightarrow \frac{1}{{\sqrt 2 }} = \frac{{\left| {a - 3b} \right|}}{{\sqrt {{a^2} + {b^2}} .\sqrt {10} }} \Leftrightarrow \sqrt 2 \left| {a - 3b} \right| = \sqrt {10} \sqrt {{a^2} + {b^2}} \\ \Leftrightarrow {\left( {a - 3b} \right)^2} = 5{a^2} + 5{b^2} \Leftrightarrow 4{a^2} - 4{b^2} + 6ab = 0\\ \Leftrightarrow 2{a^2} + 4ab - ab - 2b \Leftrightarrow \left( {2a - b} \right)\left( {a + 2b} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}b = 2a \Rightarrow \left( {a;b} \right) = \left( {1;\,2} \right) \Rightarrow \left( d \right):x + 2y - 3 = 0\\a =  - 2b \Rightarrow \left( {a;b} \right) = \left( { - 2;1} \right) \Rightarrow \left( d \right): - 2x + y + 1 = 0 \Leftrightarrow 2x - y = 1\end{array} \right.\end{array}\) 

Chọn B.

Phương pháp giải:

Góc giữa hai đường thẳng bằng góc giữa 2 VTPT (VTCP) của 2 đường thẳng đó:  \(\cos \left( {\overrightarrow a ;\overrightarrow b } \right) = \frac{{\left| {\overrightarrow a .\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\)

Lời giải chi tiết:

Ta có: \({\Delta _1}\) nhận \(\overrightarrow {{n_1}}  = \left( {1; - 2} \right)\) là một VTPT

\({\Delta _2}\) nhận \(\overrightarrow u  = \left( { - 1;2} \right)\) là một VTCP \( \Rightarrow \overrightarrow {{n_2}}  = \left( {2;1} \right)\) là 1 VTPT của \({\Delta _2}\)

Dễ thấy \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}}  = 1.2 - 2.1 = 0 \Rightarrow \overrightarrow {{n_1}}  \bot \overrightarrow {{n_2}}  \Rightarrow {\Delta _1} \bot {\Delta _2}\)

\( \Rightarrow \) Góc giữa 2 đường thẳng đó là \({90^o}\) 

Chọn D.

Phương pháp giải:

Cho đường thẳng \(\Delta :ax + by + c = 0\) và điểm \({M_0}\left( {{x_0};{y_0}} \right) \Rightarrow d\left( {{M_0};\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

Lời giải chi tiết:

Khoảng cách từ điểm \(A\left( {0;4} \right)\) đến đường thẳng \(x.\sin \alpha  + y.\cos \alpha  + 4\left( {1 - \cos \alpha } \right) = 0\) là:

\(\frac{{\left| {0.\sin \alpha  + 4.\cos \alpha  + 4\left( {1 - \cos \alpha } \right)} \right|}}{{\sqrt {{{\sin }^2}\alpha  + {{\cos }^2}\alpha } }} = \frac{{\left| {4\cos \alpha  + 4 - 4\cos \alpha } \right|}}{{\sqrt 1 }} = \frac{4}{1} = 4\)

Chọn B.

Phương pháp giải:

Đường cao \(AH \bot BC \Rightarrow \overrightarrow {BC} \)  là một VTPT của đường cao AH.

Lời giải chi tiết:

Đường cao \(AH \bot BC \Rightarrow \overrightarrow {BC}  = \left( {2;3} \right)\)  là một VTPT của đường cao AH

\( \Rightarrow \) Phương trình \(AH:\,\,2\left( {x - 1} \right) + 3\left( {y - 2} \right) = 0 \Leftrightarrow 2x + 3y - 8 = 0\)

Chọn A.

Phương pháp giải:

Đường thẳng \(\Delta \) nhận vecto \(\left( {a;\,b} \right)\) làm VTCP thì \(\Delta \) nhận vecto \(\left( {b; - a} \right) = \left( { - b;\,a} \right)\) làm VTPT.

Lời giải chi tiết:

Đường thẳng d: \(\left\{ \begin{array}{l}x =  - 4 + 5t\\y = 1 - t\end{array} \right.\) có  VTCP  \(\overrightarrow u  = \left( {5; - 1} \right)\)

Gọi \(\overrightarrow n \) là VTPT của đường thẳng \(\Delta \) cần tìm

Đường thẳng \(\Delta \) cần tìm song song với đường thẳng d: \(\left\{ \begin{array}{l}x =  - 4 + 5t\\y = 1 - t\end{array} \right.\)

\( \Rightarrow \) \(\overrightarrow n  \bot \overrightarrow u  \Rightarrow \overrightarrow n  = \left( {1;5} \right)\)

\( \Rightarrow \) Phương trình \(\Delta :\,\,x - 1 + 5y = 0 \Leftrightarrow x + 5y - 1 = 0\)

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

\(\left( {AB} \right):\,\,8x + 19y + 3 = 0.\,\,\left( {AC} \right)\) học sinh tự giải.

Phương pháp giải:

Đường thẳng trung trực của đoạn thẳng \(AB\) đi qua trung điểm \(M\) của \(AB\) và nhận \(\overrightarrow {AB} \) làm VTPT.

Phương trình đường thẳng \(d\) đi qua \(M\left( {{x_0};\,\,{y_0}} \right)\) và có VTPT \(\overrightarrow n  = \left( {A;\,\,B} \right)\) có dạng: \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) = 0.\)

Lời giải chi tiết:

Gọi \(M\)  là trung điểm \(AB\) B\( \Rightarrow \left\{ \begin{array}{l}{x_M} = \frac{{ - 3 + 1}}{2} =  - 1\\{y_M} = \frac{{6 + 3}}{2} = \frac{9}{2}\end{array} \right. \Rightarrow M\left( { - 1;\frac{9}{2}} \right)\)

Ta có: \(\overrightarrow {AB}  = \left( {4; - 3} \right)\)

Đường thẳng trung trực \(d\)  của đoạn thẳng \(AB\) đi qua trung điểm \(M\left( { - 1;\,\,\frac{9}{2}} \right)\) của \(AB\) và nhận \(\overrightarrow {AB}  = \left( {4; - 3} \right)\) làm VTPT.

\( \Rightarrow d:\,\,\,\,4\left( {x + 1} \right) - 3\left( {y - \frac{9}{2}} \right) = 0\)\( \Leftrightarrow 4x - 3y + \frac{{35}}{2} = 0\)\( \Leftrightarrow 8x - 6y + 35 = 0\)

Chọn C.

Phương pháp giải:

Bước 1: Tìm \(H\) là hình chiếu của \(M\) trên đường thẳng \(d\)                          

Bước 2: Tìm điểm \(N\) với \(H\) là trung điểm \(MN\)

Lời giải chi tiết:

Gọi \(H\) là hình chiếu của \(M\) trên đường thẳng \(d\)

Vì \(H \in d:2x + y - 5 = 0 \Rightarrow H\left( {t;5 - 2t} \right)\)

\(MH \bot d \Rightarrow \overrightarrow {MH}  = \left( {t - 1;3 - 2t} \right)\) cùng phương với VTPT \(\overrightarrow {{n_d}}  = \left( {2;1} \right)\)    

\( \Rightarrow \frac{{t - 1}}{2} = \frac{{3 - 2t}}{1} \Leftrightarrow t - 1 = 6 - 4t\)\( \Rightarrow t = \frac{7}{5} \Rightarrow H\left( {\frac{7}{5};\frac{{11}}{5}} \right)\)

Vì \(N\) đối xứng \(M\) qua \(d\) nên \(H\) là trung điểm của \(MN\)

\( \Rightarrow \left\{ \begin{array}{l}{x_N} = 2{x_H} - {x_M} = 2.\frac{7}{5} - 1 = \frac{9}{5}\\{y_N} = 2{y_H} - {y_M} = 2.\frac{{11}}{5} - 2 = \frac{{12}}{5}\end{array} \right.\)\( \Rightarrow N\left( {\frac{9}{5};\frac{{12}}{5}} \right) \Rightarrow a + b = \frac{{21}}{5}\)

Chọn D.

Phương pháp giải:

+ Lập phương trình cạnh \(BC\).

+ Xác định tọa độ đỉnh \(B\): \(\overrightarrow {BC} \,\,.\,\,\overrightarrow {AH}  = 0\)

Lời giải chi tiết:

*) \(A\left( {0;\,\,3} \right)\), \(H\left( {0;\,\,1} \right)\)\( \Rightarrow \overrightarrow {AH}  = \left( {0;\,\, - 2} \right)\)

*) Lập phương trình cạnh \(BC\)

\(\left( {BC} \right):\,\,\left\{ \begin{array}{l}{\rm{qua}}\,M\left( {1;0} \right)\\{{\vec n}_{BC}} = {{\vec u}_{AH}} = \left( {0;\,\, - 2} \right)\end{array} \right.\)

\( \Rightarrow 0.\left( {x - 1} \right) - 2.\left( {y - 0} \right) = 0 \Leftrightarrow  - 2y = 0 \Leftrightarrow y = 0\)

*) Gọi \(B\left( {b;\,\,0} \right)\), \(C\left( {2 - b;\,\,0} \right)\).

Ta có: \(\overrightarrow {BH}  = \left( { - b;\,\,1} \right)\), \(\overrightarrow {AC}  = \left( {2 - b;\,\, - 3} \right)\)

Vì \(\overrightarrow {BH} \,\,.\,\,\overrightarrow {AC}  = 0\)\( \Rightarrow \left( {2 - b} \right).\left( { - b} \right) - 3.1 = 0 \Leftrightarrow {b^2} - 2b - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}b = 3\\b =  - 1\end{array} \right.\)

Vì \(B\) có hoành độ âm nên \(b =  - 1\)

Vậy \(B\left( { - 1;\,\,0} \right).\)

Chọn  B

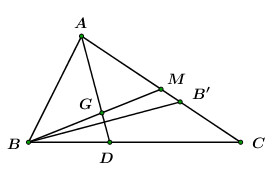
Phương pháp giải:

+) Áp dụng \(BG = 2GM\) để tìm tọa độ điểm \(M\) (\(M\) là trung điểm của \(AC\))

+) Gọi \(B'\) là điểm đối xứng của \(B\) qua phân giác góc \(A\) \( \Rightarrow B' \in AC\)

+) Phương trình cạnh \(AC\) đi qua \(M\) và \(B'\).

Lời giải chi tiết:

+) Gọi \(M\) là trung điểm của \(AC\), \(AD\) là phân giác trong góc \(A\) có phương trình: \(x - y - 1 = 0\)

+) Vì \(G\) là trọng tâm của \(\Delta ABC,\,\,BM\) là đường trung tuyến nên ta có: \(\overrightarrow {BG}  = 2\overrightarrow {GM} \)

\( \Rightarrow \left\{ \begin{array}{l}1 + 4 = 2\left( {{x_M} - 1} \right)\\1 - 1 = 2\left( {{y_M} - 1} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_M} = \frac{7}{2}\\{y_M} = 1\end{array} \right. \Rightarrow M\left( {\frac{7}{2};\,\,1} \right)\)

+) Phương trình đường thẳng \(d\) qua \(B\) và vuông góc với \(AD\)

 \( \Rightarrow \left( d \right):\,\,\,\,x + 4 + y - 1 = 0 \Leftrightarrow \,x + y + 3 = 0\)

Gọi \(I = \left( d \right) \cap AD\). Tọa độ điểm \(I\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}x - y - 1 = 0\\x + y + 3 = 0\end{array} \right. \Rightarrow I\left( { - 1;\,\, - 2} \right)\)

Gọi \(B'\) là điểm đối xứng của \(B\) qua phân giác góc \(A\) \( \Rightarrow B' \in AC\)

\( \Rightarrow \)\(I\) là trung điểm của \(BB'\)\( \Rightarrow B'\left( {2;\,\, - 5} \right)\)

Phương trình cạnh \(AC\) qua \(M\) và \(B'\) là:

\(AC:\,\,\,\frac{{x - 2}}{{\frac{7}{2} - 2}} = \frac{{y + 5}}{{1 + 5}} \Leftrightarrow 6\left( {x - 2} \right) = \frac{3}{2}\left( {y + 5} \right)\)\( \Leftrightarrow 4x - 8 = y + 5 \Leftrightarrow 4x - y - 13 = 0\)

Ta có: \(A = AC \cap AD\)\( \Rightarrow \) Tọa độ điểm \(A\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}4x - y - 13 = 0\\x - y - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 3\end{array} \right. \Rightarrow A\left( {4;\,\,3} \right)\)

Vậy \(A\left( {4;\,\,3} \right)\).

Chọn  A.

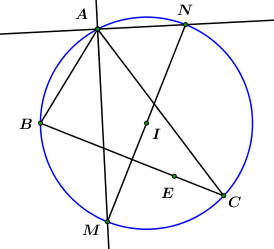
Phương pháp giải:

+) \(AN \bot AM\) (t.c phân giác của hai góc kề bù) \(\Rightarrow\) đường tròn \(\left( C \right)\) sẽ có tâm \(I\left( { - 1;\,\, - 1} \right)\)  là trung điểm \(MN\), bán kính \(R = \frac{{MN}}{2} = \sqrt 5 \) \( \Rightarrow \left( C \right):{\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} = 5\)

+) Để  tìm tọa độ \(B,\,\,C\)  ta cần thiết lập phương trình đường thẳng \(BC\) rồi cho giao với đường tròn \(\left( C \right).\)

Lời giải chi tiết:

Ta có \(AM,\,\,AN\) là hai đường phân giác trong và ngoài của \(\angle A \Rightarrow AM \bot AN\) (tính chất các đường phân giác của một góc).

\( \Rightarrow \angle MAN = {90^0}\) \( \Rightarrow MN\) là đường kính của đường tròn \(\left( C \right)\) ngoại tiếp \(\Delta ABC.\)

\( \Rightarrow MN \bot BC.\)

Ta có: \(\overrightarrow {MN}  = \left( { - 2;\,\,4} \right) =  - 2\left( {1; - 2} \right).\)

Đường thẳng \(BC\) qua \(E\) và nhận \(\overrightarrow {MN} \) làm VTPT có phương trình: \(x - 2 - 2\left( {y + 1} \right) = 0 \Leftrightarrow x - 2y - 4 = 0.\)

Gọi \(I\) là trung điểm của \(MN \Rightarrow I\left( { - 1; - 1} \right)\)

Có: \(MN = \sqrt {{{\left( { - 2} \right)}^2} + {4^2}}  = 2\sqrt 5  \Rightarrow IM = \frac{1}{2}MN = \sqrt 5 .\)

Phương trình đường tròn \(\left( C \right)\) có tâm \(I\left( { - 1;\,\, - 1} \right)\) và đường kính \(MN\) là: \(\left( C \right):\,\,\,{\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} = 5.\)

Khi đó tọa độ các điểm \(B,\,\,C\) là nghiệm của hệ phương trình:

\(\begin{array}{l}\left\{ \begin{array}{l}{\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} = 5\\x - 2y - 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2y + 4\\{\left( {2y + 5} \right)^2} + {\left( {y + 1} \right)^2} = 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 2y + 4\\5{y^2} + 22y + 21 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}y =  - \frac{7}{5}\\y =  - 3\end{array} \right.\\x = 2y + 4\end{array} \right. \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = \frac{6}{5}\\y =  - \frac{7}{5}\end{array} \right.\\\left\{ \begin{array}{l}x =  - 2\\y =  - 3\end{array} \right.\end{array} \right.\end{array}\)

Vì \(C\) có hoành độ dương \( \Rightarrow C\left( {\frac{6}{5}; - \frac{7}{5}} \right);\,\,\,B\left( { - 2; - 3} \right).\)

Chọn  D.

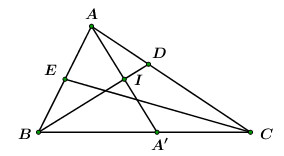
Phương pháp giải:

+ Lấy \(E\) là trung điểm của \(AB\).

+ \(A'\) là điểm đối xứng của \(A\) qua \(BD\).

+ Viết phương trình cạnh \(BC.\)

Lời giải chi tiết:

Gọi \(E\) là trung điểm của \(AB\), \(A'\) là điểm đối xứng của \(A\) qua \(BD\)\( \Rightarrow A' \in BC\)

Vì \(B \in \left( {BD} \right):\,\,x + y - 2 = 0 \Rightarrow B\left( {b;\,\,2 - b} \right)\)\( \Rightarrow E\left( {\frac{{b + 1}}{2};\,\, - \frac{{1 + b}}{2}} \right) \in CE\)

\(\begin{array}{l} \Rightarrow \frac{{b + 1}}{2} + 8.\left( { - \frac{{1 + b}}{2}} \right) - 7 = 0\\ \Leftrightarrow b + 1 - 8 - 8b - 14 = 0\\ \Leftrightarrow  - 7b = 21\\ \Leftrightarrow b =  - 3\\ \Rightarrow B\left( { - 3;\,\,5} \right).\end{array}\)

Phương trình đường thẳng \(AA'\) đi qua \(A\left( {1; - 3} \right)\) và nhận \(\overrightarrow {{u_{BD}}}  = \left( {1; - 1} \right)\) làm VTPT là:

\(AA':\,\,\,x - 1 - \left( {y + 3} \right) = 0 \Leftrightarrow x - y - 4 = 0\)

Khi đó tọa độ điểm \(I = BD \cap AA'\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}x - y - 4 = 0\\x + y - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y =  - 1\end{array} \right. \Rightarrow I\left( {3; - 1} \right).\)

Vì \(A'\) là điểm đối xứng của \(A\) qua \(BD \Rightarrow I\) là trung điểm của \(AA'\) \( \Rightarrow A'\left( {5;\,\,1} \right)\)

Phương trình đường thẳng \(BC\) qua \(A'\left( {5;\,\,1} \right)\) và \(B\left( { - 3;\,\,5} \right)\) là:

\(BC:\,\,\,\,\frac{{x + 3}}{{5 + 3}} = \frac{{y - 5}}{{1 - 5}} = 0\)\( \Leftrightarrow  - 4\left( {x + 3} \right) = 8\left( {y - 5} \right)\)\( \Leftrightarrow x + 2y - 7 = 0\)

Ta có: \(C = CE \cap BC \Rightarrow \) Tọa độ điểm \(C\) là nghiệm của hệ phương trình:  \(\left\{ \begin{array}{l}x + 2y - 7 = 0\\x + 8y - 7 = 0\end{array} \right. \Rightarrow C\left( {7;\,\,0} \right)\)

Chọn  A.

Phương pháp giải:

+ Viết phương trình đường thẳng \(AB\).

+ \(B = AB \cap BN\)

Lời giải chi tiết:

Ta có: \(AB \bot CH \Rightarrow \left( {AB} \right):x + y + c = 0\)

Mà \(A\left( {1; - 2} \right) \in \left( {AB} \right) \Rightarrow 1 - 2 + c = 0 \Rightarrow c = 1\). Suy ra \(\left( {AB} \right):x + y + 1 = 0\)

Có \(B = AB \cap BN \Rightarrow N\) là nghiệm hệ phương trình \(\left\{ \begin{array}{l}x + y + 1 = 0\\2x + y + 5 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x =  - 4\\y = 3\end{array} \right. \Rightarrow B\left( { - 4;3} \right)\).

Chọn  C

Phương pháp giải:

+ \(C \in \left( \Delta  \right):\,\,\left\{ \begin{array}{l}x = 1 + t\\y = 2 + t\end{array} \right. \Rightarrow \) Biểu diễn tọa độ điểm \(C\) theo \(t\).

+ \(\Delta ACB\) cân tại \(C\,\, \Leftrightarrow \,\,CA = CB\)

Lời giải chi tiết:

Theo đề bài, \(C \in \Delta  \Rightarrow C\left( {1 + t;\,\,2 + t} \right) \Rightarrow \left\{ \begin{array}{l}\overrightarrow {CA}  = \left( { - 2 - t;\,\, - t} \right)\\\overrightarrow {CB}  = \left( {2 - t;\,\, - 1 - t} \right)\end{array} \right.\)

\(\Delta ACB\) cân tại \(C\)\( \Leftrightarrow \,\,CA = CB \Leftrightarrow \sqrt {{{\left( { - 2 - t} \right)}^2} + {{\left( { - t} \right)}^2}}  = \sqrt {{{\left( {2 - t} \right)}^2} + {{\left( { - 1 - t} \right)}^2}} \)

\( \Leftrightarrow {\left( { - 2 - t} \right)^2} + {\left( { - t} \right)^2} = {\left( {2 - t} \right)^2} + {\left( { - 1 - t} \right)^2}\)\( \Leftrightarrow 4 + 4t + {t^2} + {t^2} = 4 - 4t + {t^2} + 1 + 2t + {t^2}\)

\( \Leftrightarrow 4 + 4t + {t^2} + {t^2} - 4 + 4t - {t^2} - 1 - 2t - {t^2} = 0\)

\( \Leftrightarrow 6t - 1 = 0 \Leftrightarrow t = \frac{1}{6}\)\( \Rightarrow C\left( {\frac{7}{6};\,\,\frac{{13}}{6}} \right)\)

Chọn  A

Phương pháp giải:

+ \(A = AC \cap d\)

+ \(M\) là trung điểm của cạnh \(AC\)

+ \(B = BH \cap BC\)

+ Xác định tọa độ trọng tâm \(G\) theo CT: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right.\)

Lời giải chi tiết:

*) Xác định tọa độ đỉnh \(A\)

+) Lập phương trình cạnh \(AC\)

\(\left( {AC} \right):\,\,\left\{ \begin{array}{l}{\rm{qua}}\,M\left( {1;\,\,1} \right)\\{{\vec n}_{AC}} = {{\vec u}_{BH}} = \left( {1;\,\, - 1} \right)\end{array} \right.\)

\( \Rightarrow 1.\left( {x - 1} \right) - 1.\left( {y - 1} \right) = 0 \Leftrightarrow x - 1 - y + 1 = 0 \Leftrightarrow x - y = 0\)

Vì \(A = AC \cap d\) nên tọa độ giao điểm \(A\left( {{x_A};\,\,{y_A}} \right)\) là nghiệm của hệ phương trình:

\(\,\left\{ \begin{array}{l}x - 4y - 2 = 0\\x - y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 4y = 2\\x - y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{ - 2}}{3}\\y = \frac{{ - 2}}{3}\end{array} \right. \Rightarrow A\left( {\frac{{ - 2}}{3};\,\,\,\frac{{ - 2}}{3}} \right)\)

*) \(A\left( { - \frac{2}{3};\,\, - \frac{2}{3}} \right);\,\,M\left( {1;\,\,1} \right);\,C\left( {{x_C};\,\,{y_C}} \right)\)

Vì \(M\) là trung điểm của \(AC\) nên ta có:

\(\left\{ \begin{array}{l}1 = \frac{{ - \frac{2}{3} + {x_C}}}{2}\\1 = \frac{{ - \frac{2}{3} + {y_C}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2 =  - \frac{2}{3} + {x_C}\\2 =  - \frac{2}{3} + {y_C}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = \frac{8}{3}\\{y_C} = \frac{8}{3}\end{array} \right. \Rightarrow C\left( {\frac{8}{3};\,\,\frac{8}{3}} \right)\)

*) Lập phương trình cạnh \(BC\)

\(\left( {BC} \right):\,\,\left\{ \begin{array}{l}{\rm{qua}}\,\,C\left( {\frac{8}{3};\,\,\frac{8}{3}} \right)\\{{\vec n}_{BC}} = {{\vec n}_d} = \left( {1;\,\, - 4} \right)\end{array} \right.\)
\( \Rightarrow 1.\left( {x - \frac{8}{3}} \right) - 4.\left( {y - \frac{8}{3}} \right) = 0 \Leftrightarrow x - \frac{8}{3} - 4y + \frac{{32}}{3} = 0 \Leftrightarrow 3x - 12y + 24 = 0\)

Vì \(B = BH \cap BC\) nên tọa độ điểm \(B\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}3x - 12y + 24 = 0\\x + y + 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x - 12y =  - 24\\x + y =  - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 4\\y = 1\end{array} \right. \Rightarrow B\left( { - 4;\,\,1} \right)\)

*) Xác định tọa độ trọng tâm \(G\left( {{x_G};\,\,{y_G}} \right)\):

\(\left\{ \begin{array}{l}{x_G} = \frac{{ - \frac{2}{3} + \left( { - 4} \right) + \frac{8}{3}}}{3}\\{y_G} = \frac{{ - \frac{2}{3} + 1 + \frac{8}{3}}}{3}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_G} =  - \frac{2}{3}\\{y_G} = 1\end{array} \right. \Rightarrow G\left( { - \frac{2}{3};\,\,1} \right)\)

Vậy \(G\left( { - \frac{2}{3};\,\,1} \right).\)

Chọn  D

Phương pháp giải:

+) Xác định tọa độ điểm \(E\) (\(E\) là điểm đối xứng với \(H\) qua đường phân giác \(BD\))

+) Viết phương trình đường thẳng \(AB\)\( \Rightarrow \) xác định tọa độ điểm \(B\)

+) Từ tọa độ điểm \(M\) và \(B\)\( \Rightarrow \) Xác định tọa độ điểm \(A\).

Lời giải chi tiết:

*) Phương trình đường phân giác \(BD:\,\,x + y - 5 = 0\)\( \Rightarrow {\vec n_{BD}} = \left( {1;\,\,1} \right),\,\,{\vec u_{BD}} = \left( { - 1;\,\,1} \right)\)

*) Gọi \(E\) là điểm đối xứng của \(H\) qua \(BD\).

Phương trình đường thẳng \(EH\):

+) Vì \(EH \bot BD\)\( \Rightarrow \) Phương trình \(EH\): \( - x + y + c = 0\)

+) \(H\left( { - 4;\,\,1} \right) \in EH \Rightarrow  - \left( { - 4} \right) + 1 + c = 0\)\( \Leftrightarrow 5 + c = 0 \Leftrightarrow c =  - 5\)

\( \Rightarrow \) Phương trình \(EH:\,\, - x + y - 5 = 0\)

*) Gọi \(BD \cap EH = I\). Tọa độ điểm \(I\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}x + y - 5 = 0\\ - x + y - 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y = 5\\ - x + y = 5\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 5\end{array} \right. \Rightarrow I\left( {0;\,\,5} \right)\)\( \Rightarrow E\left( {4;\,\,9} \right)\)

*) Phương trình đường thẳng \(AB\) đi qua \(M\left( {\frac{{17}}{5};\,\,12} \right)\) nhận \({\vec n_{ME}} = \left( {3;\,\,\frac{3}{5}} \right)\) là VTPT là:

\(3.\left( {x - \frac{{17}}{5}} \right) + \frac{3}{5} \cdot \left( {y - 12} \right) = 0\)\( \Leftrightarrow 3x - \frac{{51}}{5} + \frac{{3y}}{5} - \frac{{36}}{5} = 0\)\( \Leftrightarrow 15x + 3y - 87 = 0\)

*) Tọa độ điểm \(B\)là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}15x + 3y - 87 = 0\\x + y - 5 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 6\\y =  - 1\end{array} \right. \Rightarrow B\left( {6;\,\, - 1} \right)\)

Mà \(M\left( {\frac{{17}}{5};\,\,12} \right)\) là trung điểm của \(AB\) nên ta có: \(\left\{ \begin{array}{l}{x_A} = 2.\frac{{17}}{5} - 6\\{y_A} = 2.12 + 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_A} = \frac{4}{5}\\{y_A} = 25\end{array} \right. \Rightarrow A\left( {\frac{4}{5};\,\,25} \right)\)

Vậy \(A\left( {\frac{4}{5};\,\,25} \right)\).

Chọn  D.

Phương pháp giải:

+) Xác định tọa độ của điểm \(A\)

+) Gọi \(C'\) là điểm đối xứng của \(C\) qua phân giác \(AD\)\( \Rightarrow C' \in AB\)

+) Viết phương trình đường thẳng \(AB\) nhận \(\overrightarrow {AC'} \) là VTCP

Lời giải chi tiết:

+) Phương trình đường phân giác \(AD\): \(x + 2y - 5 = 0\)\( \Rightarrow {\vec n_{AD}} = \left( {1;\,\,2} \right),\,\,{\vec u_{AD}} = \left( {2;\,\, - 1} \right)\,\)

+) Phương trình đường trung tuyến \(AM:\,\,4x + 13y - 10 = 0\)

+) Vì \(A\) là giao điểm của \(AD\) và \(AM\) nên tọa độ điểm \(A\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}x + 2y - 5 = 0\\4x + 13y - 10 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 9\\y =  - 2\end{array} \right. \Rightarrow A\left( {9;\,\, - 2} \right)\)

+) Gọi \({C_1}\) là điểm đối xứng của \(C\) qua \(AD\)\( \Rightarrow {C_1} \in AB\)

Phương trình tổng quát của đường thẳng \(C{C_1}\) đi qua \(C\left( {4;\,\,3} \right)\) nhận  \({\vec u_{AD}} = \left( {2;\,\, - 1} \right)\,\) là VTPT:

\(C{C_1}:\,\,\,2\left( {x - 4} \right) - \left( {y - 3} \right) = 0\)\( \Leftrightarrow 2x - 8 - y + 3 = 0\)\( \Leftrightarrow 2x - y - 5 = 0\)

+) Gọi \(J = C{C_1} \cap AD\).

Tọa độ của \(J\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}2x - y - 5 = 0\\x + 2y - 5 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 3\\y = 1\end{array} \right. \Rightarrow J\left( {3;\,\,1} \right)\)

\( \Rightarrow \) Tọa độ của điểm \({C_1}\) là: \(\left\{ \begin{array}{l}{x_{{C_1}}} = 2.3 - 4\\{y_{{C_1}}} = 2.1 - 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_{{C_1}}} = 2\\{y_{{C_1}}} =  - 1\end{array} \right. \Rightarrow {C_1}\left( {2;\,\, - 1} \right)\)

+)  \(\left. \begin{array}{l}A\left( {9;\,\, - 2} \right)\\{C_1}\left( {2;\,\, - 1} \right)\end{array} \right\} \Rightarrow \overrightarrow {A{C_1}} \left( { - 7;\,\,1} \right)\)

Phương trình đường thẳng \(AB\) đi qua \(A\left( {9;\,\, - 2} \right)\) và nhận \({\vec n_{A{C_1}}} = \left( {1;\,\,7} \right)\) là VTPT là:

\(AB:\,\,\,\,\,x - 9 + 7\,\left( {y + 2} \right) = 0\)\( \Leftrightarrow x - 9 + 7y + 14 = 0\)\( \Leftrightarrow x + 7y + 5 = 0\)

Vậy phương trình đường thẳng \(AB\) là: \(x + 7y + 5 = 0\)

Chọn B.

Phương pháp giải:

Cho hai điểm \(A\left( {{x_A};\,\,{y_A}} \right)\); \(B\left( {{x_B};\,\,{y_B}} \right)\)\( \Rightarrow AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \)

Lời giải chi tiết:

Gọi \(A\left( {a;\,\,0} \right),\,\,B\left( {0;\,\,b} \right)\) lần lượt là giao điểm của đường thẳng \(\Delta \) và trục \(Ox\), \(Oy\).

+) Vì \(A\left( {a;\,\,0} \right) \in \left( \Delta  \right):\,\,\frac{x}{3} + \frac{y}{4} = 1\) nên ta có \(\frac{a}{3} + \frac{0}{4} = 1 \Leftrightarrow \frac{a}{3} = 1 \Leftrightarrow a = 3\)

\( \Rightarrow A\left( {3;\,\,0} \right)\)

+) Vì \(B\left( {0;\,\,b} \right) \in \left( \Delta  \right):\,\frac{x}{3}\, + \frac{y}{4} = 1\) nên ta có \(\frac{0}{3} + \frac{b}{4} = 1 \Rightarrow \frac{b}{4} = 1 \Leftrightarrow b = 4\)

\( \Rightarrow B\left( {0;\,\,4} \right)\)

Ta có: \(A\left( {3;\,\,0} \right),\,\,B\left( {0;\,\,4} \right) \Rightarrow AB = \sqrt {{{\left( {0 - 3} \right)}^2} + {{\left( {4 - 0} \right)}^2}}  = \sqrt {{3^2} + {4^2}}  = \sqrt {25}  = 5\)

Chọn  D

Phương pháp giải:

+ Viết phương trình đường thẳng \(AB\), \(CD.\)

+ Xác định tọa độ giao điểm của \(AB,\,\,CD.\)

Lời giải chi tiết:

+) \(\left( {AB} \right):\left\{ \begin{array}{l}{\rm{qua}}\,\,A\left( { - 3;\,\,1} \right)\\{{\vec n}_{AB}} = \left( {2;\,\, - 3} \right)\end{array} \right.\)

\( \Rightarrow \left( {AB} \right):\,\,\,2\,.\,\left( {x + 3} \right) - 3\,.\,\left( {y - 1} \right) = 0\, \Leftrightarrow 2x + 6 - 3y + 3 = 0 \Leftrightarrow 2x - 3y + 9 = 0\)

+) \(\left( {CD} \right):\left\{ \begin{array}{l}{\rm{qua}}\,\,C\left( { - 6;\,\,0} \right)\\{{\vec n}_{CD}} = \left( {1;\,\, - 1} \right)\end{array} \right.\)

\( \Rightarrow \left( {CD} \right):\,\,1.\left( {x + 6} \right) - 1\,.\,\left( {y - 0} \right) = 0\, \Leftrightarrow x - y + 6 = 0\)

+) Gọi \(E = AB \cap CD\).

Tọa độ giao điểm \(E\) của \(AB\) và \(CD\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}2x - 3y + 9 = 0\\x - y + 6 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - 3y =  - 9\\x - y =  - 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 9\\y =  - 3\end{array} \right. \Rightarrow E\left( { - 9;\,\, - 3} \right)\)

Chọn  B

Phương pháp giải:

+) Xác định tọa độ điểm \(C\).

+) Viết phương trình đường tròn đi qua ba điểm \(A,\,\,B,\,\,C\).

Lời giải chi tiết:

+) Gọi \(E\) là điểm đối xứng của \(A\) qua \(d\)\( \Rightarrow E \in BC\)

Kẻ \(AH \bot d\) \( \Rightarrow \left( {AH} \right):\,\,\left\{ \begin{array}{l}A\left( {3;\,\,5} \right)\\{{\vec n}_{AH}} = {{\vec u}_d} = \left( { - 2;\,\,1} \right)\end{array} \right.\)

\( \Rightarrow AH:\,\,\, - 2\left( {x - 3} \right) + y - 5 = 0\)\( \Leftrightarrow  - 2x + 6 + y - 5 = 0\)\( \Leftrightarrow  - 2x + y + 1 = 0\)

Tọa độ điểm \(H\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l} - 2x + y + 1 = 0\\x + 2y - 8 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2x + y + 1 = 0\\2x + 4y - 16 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right. \Rightarrow H\left( {2;\,\,3} \right)\)

\( \Rightarrow \) \(H\) là trung điểm của \(AE\)\( \Rightarrow \left\{ \begin{array}{l}{x_E} = 2.2 - 3\\{y_E} = 2.3 - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_E} = 1\\{y_E} = 1\end{array} \right. \Rightarrow E\left( {1;\,\,1} \right)\)

+) Phương trình cạnh \(\left( {BC} \right):\,\,\left\{ \begin{array}{l}{\rm{qua}}\,\,E\left( {1;\,\,1} \right)\\{{\vec n}_{BC}} = \left( {4;\,\,3} \right)\end{array} \right.\)

\( \Rightarrow \left( {BC} \right):\,\,4\left( {x - 1} \right) + 3\left( {y - 1} \right) = 0\)\( \Leftrightarrow 4x + 3y - 7 = 0\)

Tọa độ điểm \(C\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}4x + 3y - 7 = 0\\x + 2y - 8 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 2\\y = 5\end{array} \right. \Rightarrow C\left( { - 2;\,\,5} \right)\)

Gọi phương trình đường tròn ngoại tiếp tam giác \(ABC\) có dạng: \({x^2} + {y^2} - 2ax - 2by + c = 0,\,\,{a^2} + {b^2} - c > 0\)

Do đó, ta có hệ phương trình: \(\left\{ \begin{array}{l}4a - 10b + c =  - 29\\ - 6a - 10b + c =  - 34\\ - 8a + 6b + c =  - 25\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{2}\\b = \frac{5}{8}\\c = \frac{{ - 99}}{4}\end{array} \right.\)

Vậy phương trình đường tròn ngoại tiếp tam giác \(ABC\) là:

\({x^2} + {y^2} - x - \frac{5}{4}y - \frac{{99}}{4} = 0 \Leftrightarrow 4{x^2} + 4{y^2} - 4x - 5y - 99 = 0\)

Chọn  B.

Phương pháp giải:

Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) biết phương trình cạnh \(BC:x + y - 2 = 0\), hai đường cao \(BB':x - 3 = 0\) và \(CC':2x - 3y + 6 = 0\). Tọa độ các đỉnh của tam giác \(ABC\) là:

Lời giải chi tiết:

*) Xác định tọa độ đỉnh \(B\).

Vì \(B = BC \cap BB'\) nên tọa độ đỉnh \(B\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}x + y - 2 = 0\\x - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y =  - 1\end{array} \right. \Rightarrow B\left( {3;\,\, - 1} \right)\)

*) Xác định tọa độ đỉnh \(C\).

Vì \(C = CC' \cap BC\) nên tọa độ đỉnh \(C\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}x + y - 2 = 0\\2x - 3y + 6 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y = 2\\2x - 3y =  - 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 2\end{array} \right. \Rightarrow C\left( {0;\,\,2} \right)\)

*) Xác định tọa độ đỉnh \(A\).

+) Lập phương trình cạnh \(AB\)

\(\left( {AB} \right):\,\,\left\{ \begin{array}{l}{\rm{qua}}\,\,B\left( {3; - 1} \right)\\{{\vec n}_{AB}} = {{\vec u}_{CC'}} = \left( {3;\,\,2} \right)\end{array} \right.\)

\( \Rightarrow 3.\left( {x - 3} \right) + 2.\left( {y + 1} \right) = 0 \Leftrightarrow 3x - 9 + 2y + 2 = 0 \Leftrightarrow 3x + 2y - 7 = 0\)

+) Lập phương trình cạnh \(AC\)

\(AC:\,\,\left\{ \begin{array}{l}{\rm{qua}}\,\,C\left( {0;\,\,2} \right)\\{{\vec n}_{AC}} = {{\vec u}_{BB'}} = \left( {0;\,\,1} \right)\end{array} \right.\)

\( \Rightarrow 0.\left( {x - 0} \right) + 1.\left( {y - 2} \right) = 0 \Leftrightarrow y - 2 = 0\)

Vì \(A = AB \cap AC \Rightarrow \)Tọa độ đỉnh \(A\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}3x + 2y - 7 = 0\\y - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x + 2y = 7\\y - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right. \Rightarrow A\left( {1;\,\,2} \right)\)

Vậy \(A\left( {1;\,\,2} \right),\,\,B\left( {3;\,\, - 1} \right),\,\,C\left( {0;\,\,2} \right)\).

Chọn  D

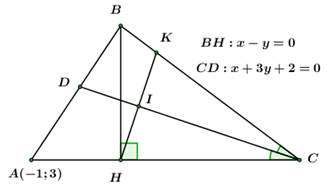
Phương pháp giải:

+ Viết phương trình đoạn chắn đi qua \(M\) và cắt trục \(Ox\), \(Oy\) lần lượt tại hai điểm \(A\) và \(B\).

+  Gọi \(N\) là trung điểm của \(AB\), tam giác \(IAB\) cân tại \(I\)\( \Leftrightarrow IN \bot AB\)

Lời giải chi tiết:

Giả sử đường thẳng \(d\) đi qua \(M\) cắt trục \(Ox\) và \(Oy\)lần lượt tại hai điểm \(A\left( {a;\,\,0} \right)\) và \(B\left( {0;\,\,b} \right)\), \(a\,.\,\,b \ne 0\).

Phương trình đường thẳng \(d\) có dạng: \(\frac{x}{a} + \frac{y}{b} = 1\)

Vì đường thẳng \(d\) đi qua \(M\left( {3;\,\,1} \right)\) nên ta có: \(\frac{3}{a} + \frac{1}{b} = 1\)

Gọi \(N\left( {{x_N};\,\,{y_N}} \right)\) là trung điểm của \(AB\)\( \Rightarrow \left\{ \begin{array}{l}{x_N} = \frac{{a + 0}}{2}\\{y_N} = \frac{{b + 0}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_N} = \frac{a}{2}\\{y_N} = \frac{b}{2}\end{array} \right. \Rightarrow N\left( {\frac{a}{2};\,\,\frac{b}{2}} \right)\)

Ta có:

+) \(I\left( {2;\,\, - 2} \right);\,\,N\left( {\frac{a}{2};\,\,\frac{b}{2}} \right) \Rightarrow \overrightarrow {IN}  = \left( {\frac{a}{2} - 2;\frac{b}{2} + 2} \right) = \left( {\frac{{a - 4}}{2};\frac{{b + 4}}{2}} \right) = \left( {a - 4;\,\,b + 4} \right)\)

+) \(A\left( {a;\,\,0} \right),\,\,B\left( {0;\,\,b} \right) \Rightarrow \overrightarrow {AB}  = \left( { - a;\,\,b} \right)\)

\(\Delta IAB\) cân tại \(I\)\( \Leftrightarrow IN \bot AB \Leftrightarrow \overrightarrow {IN.} \overrightarrow {AB}  = 0\)\( \Leftrightarrow \left( {a - 4} \right)\left( { - a} \right) + b\left( {b + 4} \right) = 0\)

\( \Leftrightarrow  - {a^2} + 4a + {b^2} + 4b = 0\)

\( \Leftrightarrow \left( {{b^2} - {a^2}} \right) + \left( {4a + 4b} \right) = 0\)

\( \Leftrightarrow \left( {b - a} \right)\left( {b + a} \right) + 4\left( {b + a} \right) = 0\)

\( \Leftrightarrow \left( {b - a + 4} \right)\left( {b + a} \right) = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}b - a + 4 = 0\\b + a = 0\end{array} \right.\)

- Trường hợp 1: \(b - a + 4 = 0 \Rightarrow a - b = 4 \Leftrightarrow a = b + 4\)

Thay \(a = b + 4\) vào CT \(\frac{3}{a} + \frac{1}{b} = 1\) ta có:

\(\frac{3}{{b + 4}} + \frac{1}{b} = 1 \Leftrightarrow 3b + \left( {b + 4} \right) = b\left( {b + 4} \right) \Leftrightarrow 3b + b + 4 = {b^2} + 4b \Leftrightarrow {b^2} - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}b =  - 2\\b = 2\end{array} \right.\)

Với \(b =  - 2\) \( \Rightarrow a = 2\). Phương trình đường thẳng \(d\) là: \(\frac{x}{2} + \frac{y}{{ - 2}} = 1 \Leftrightarrow \frac{x}{2} - \frac{y}{2} = 1 \Leftrightarrow x - y - 2 = 0\)

Với \(b = 2 \Rightarrow a = 6\). Phương trình đường thẳng \(d\) là: \(\frac{x}{6} + \frac{y}{2} = 1 \Leftrightarrow \frac{x}{6} + \frac{y}{2} = 1 \Leftrightarrow x + 3y - 6 = 0\)

- Trường hợp 2: Thay \(b =  - a\) vào công thức \(\frac{3}{a} + \frac{1}{b} = 1\) ta được: \(\frac{3}{a} - \frac{1}{a} = 1 \Leftrightarrow \frac{2}{a} = 1 \Rightarrow a = 2\)

Với \(a = 2 \Rightarrow b =  - 2\). Phương trình đường thẳng \(d\) là: \(\frac{x}{2} + \frac{y}{{ - 2}} = 1 \Leftrightarrow \frac{x}{2} - \frac{y}{2} = 1 \Leftrightarrow x - y - 2 = 0\)

Vậy phương trình đường thẳng \(d\) là \(x - y - 2 = 0\) hoặc \(x + 3y - 6 = 0.\)

Chọn  C.

Phương pháp giải:

+) Xác định tọa độ điểm \(A\)

+) Xác định độ điểm \(B\) (Viết phương trình đường cao\(BH\))

+) Viết phương trình cạnh \(BC\) đi qua \(B\) và nhận \(\overrightarrow {AH} \) là VTPT.

Lời giải chi tiết:

Ta có \(A = AB \cap AC \Rightarrow A\left( {0;3} \right)\) \( \Rightarrow \overrightarrow {AH}  = \left( {1; - 2} \right)\)

Ta có \(BH \bot AC \Rightarrow \left( {BH} \right):7x - 4y + d = 0\)

Mà \(H\left( {1;1} \right) \in \left( {BH} \right) \Rightarrow d =  - 3\) suy ra \(\left( {BH} \right):7x - 4y - 3 = 0\)

Có \(B = AB \cap BH \Rightarrow B\left( { - 5; - \frac{{19}}{2}} \right)\)

Phương trình \(\left( {BC} \right)\) nhận \(\overrightarrow {AH}  = \left( {1; - 2} \right)\) là VTPT và qua \(B\left( { - 5; - \frac{{19}}{2}} \right)\)

Suy ra \(\left( {BC} \right):\left( {x + 5} \right) - 2\left( {y + \frac{{19}}{2}} \right) = 0 \Leftrightarrow x - 2y - 14 = 0\)

Chọn  D.

Phương pháp giải:

+) Xác định tọa độ giao điểm \(I\) của hai đường thẳng \({d_1}\) và \({d_2}\).

+) Viết phương trình đường thẳng đi qua \(M\left( {{x_0};\,\,{y_0}} \right) \in {d_1}\) và vuông góc với \({d_2}\). Sau đó, xác định tọa độ giao điểm \(E\left( {a;\,\,b} \right)\) của \({d_2}\) và \(\left( \Delta  \right)\)

+) Xác định tọa độ điểm \(N\left( {{x_1};\,\,{y_1}} \right)\) là điểm đối xứng với \(M\left( {{x_0};\,\,{y_0}} \right)\) qua \(E\left( {a;\,\,b} \right)\).

+) Viết phương trình đường thẳng qua \(I\) và nhận \(\overrightarrow {IN} \) là VTPT.

Lời giải chi tiết:

Gọi \(I\) là giao điểm của hai đường thẳng \({d_1},\,\,{d_2}\).

+) Tọa độ điểm \(I\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}x + 2y - 1 = 0\\x - 3y + 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - \frac{3}{5}\\y = \frac{4}{5}\end{array} \right.\)\( \Rightarrow I\left( { - \frac{3}{5};\frac{4}{5}} \right).\)

+) Lấy điểm \(M\left( {1;0} \right) \in {d_1}\). Đường thẳng \(\Delta \) qua \(M\) và vuông góc với \({d_2}\) có phương trình:

\(3x + y - 3 = 0.\)

+) Gọi \(H = \Delta  \cap {d_2}\), suy ra tọa độ điểm\(H\) là nghiệm của hệ: \(\left\{ \begin{array}{l}x - 3y + 3 = 0\\3x + y - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{3}{5}\\y = \frac{6}{5}\end{array} \right.\)\( \Rightarrow H\left( {\frac{3}{5};\frac{6}{5}} \right).\)

\( \Rightarrow N\left( {\frac{1}{5};\frac{{12}}{5}} \right)\) là điểm đối xứng của \(M\) qua \({d_2}\).

Phương trình đường thẳng \(d:\left\{ \begin{array}{l}{\rm{qua }}I\left( { - \frac{3}{5};\frac{4}{5}} \right)\\\overrightarrow {{n_d}}  = \overrightarrow {{n_{IN}}}  = \left( {2; - 1} \right)\end{array} \right.\) có dạng: \(2x - y + 2 = 0.\)

Chọn  B.

Phương pháp giải:

+) Gọi \(E\) là điểm đối xứng với \(M\) qua \(AD\)\( \Rightarrow E \in AB\)

+) Có \(CH\) là đường cao, viết được phương trình cạnh \(AB.\) Xác định tọa độ đỉnh \(A\). Từ đó, xác địnhh được tọa độ đỉnh \(B,\,\,C.\)

Lời giải chi tiết:

+) Gọi \(E\) là điểm đối xứng với \(M\) qua \(AD\)\( \Rightarrow E \in AB\) và \(E\left( {2;\,\, - 1} \right)\)

+) Phương trình đường cao \(\left( {CH} \right):\,\,x - 2y + 5 = 0 \Rightarrow {\vec n_{CH}} = \left( {1;\,\, - 2} \right) \Rightarrow {\vec u_{CH}} = \left( {2;\,\,1} \right)\)

+) Phương trình cạnh \(\left( {AB} \right):\left\{ \begin{array}{l}{\rm{qua}}\,\,E\left( {2;\,\, - 1} \right)\\{{\vec n}_{AB}} = {{\vec u}_{CH}} = \left( {2;\,\,1} \right)\end{array} \right.\)

\( \Rightarrow AB:\,\,\,2\left( {x - 2} \right) + y + 1 = 0\)\( \Leftrightarrow 2x - 4 + y + 1 = 0\)\( \Leftrightarrow 2x + y - 3 = 0\)

+) \(A = AB \cap AD\)\( \Rightarrow \) Tọa độ điểm \(A\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}x + y - 2 = 0\\2x + y - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 1\end{array} \right. \Rightarrow A\left( {1;\,\,1} \right)\)

+) Gọi \(B\left( {t;\,\,3 - 2t} \right);\,\,A\left( {1;\,\,1} \right);\,\,M\left( {3;\,\,0} \right)\)

\( \Rightarrow AB = \sqrt {{{\left( {t - 1} \right)}^2} + {{\left( {2 - 2t} \right)}^2}} \) và  \(AM = \sqrt {{{\left( {3 - 1} \right)}^2} + {{\left( {0 - 1} \right)}^2}}  = \sqrt {4 + 1}  = \sqrt 5 \)

Theo đề bài, \(AB = 2AM\)\( \Rightarrow \sqrt {{{\left( {t - 1} \right)}^2} + {{\left( {2 - 2t} \right)}^2}}  = 2\sqrt 5 \)\( \Leftrightarrow \sqrt {{{\left( {t - 1} \right)}^2} + 4{{\left( {t - 1} \right)}^2}}  = 2\sqrt 5 \)

\( \Leftrightarrow \sqrt 5 .\left| {t - 1} \right| = 2\sqrt 5  \Rightarrow \left[ \begin{array}{l}t - 1 = 2\\t - 1 =  - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = 3\\t =  - 1\end{array} \right.\)

\( \Rightarrow B\left( {3;\,\, - 3} \right)\) hoặc \(B\left( { - 1;\,\,5} \right)\)

Mặt khác, \(AB = 2AM\)\( \Rightarrow E\) là trung điểm của \(AB\)\( \Rightarrow B\left( {3;\,\, - 3} \right)\)

Phương trình đường thẳng \(AC\) đi qua \(A\left( {1;\,\,1} \right)\) và \(M\left( {3;\,\,0} \right)\) là:

\(AC:\,\,\,\frac{{x - 1}}{{3 - 1}} = \frac{{y - 1}}{{0 - 1}} \Leftrightarrow x - 1 + 2y - 2 = 0\) \( \Leftrightarrow x + 2y - 3 = 0.\)

Tọa độ điểm \(C\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}x + 2y - 3 = 0\\x - 2y + 5 = 0\end{array} \right. \Rightarrow C\left( { - 1;\,\,2} \right)\)

Vậy \(A\left( {1;\,\,1} \right),\,\,B\left( {3;\,\, - 3} \right),\,\,C\left( { - 1;\,\,2} \right).\)

Chọn  A.

Phương pháp giải:

+) Xác định tọa độ trực tâm \({H_1}\) của \(\Delta ABC\).

+) Viết phương trình đường thẳng \(A{H_1}\).

Lời giải chi tiết:

Kẻ đường cao \(AI\).

Gọi \({H_1}\) là trực tâm của \(\Delta ABC\), khi đó tọa độ điểm \({H_1}\) là nghiệm của hệ phương trình:\(\left\{ \begin{array}{l}2x + y - 4 = 0\\x - y - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{7}{3}\\y =  - \frac{2}{3}\end{array} \right. \Rightarrow {H_1}\left( {\frac{7}{3};\,\, - \frac{2}{3}} \right)\) \( \Rightarrow \overrightarrow {A{H_1}}  = \left( { - \frac{5}{3};\frac{4}{3}} \right)\)

\(AI\) qua \({H_1}\left( {\frac{7}{3}; - \frac{2}{3}} \right)\) và nhận \(\vec n = \left( {4;5} \right)\) làm VTPT \( \Rightarrow AI:4\left( {x - \frac{7}{3}} \right) + 5\left( {y + \frac{2}{3}} \right) = 0\)\( \Leftrightarrow 4x + 5y - 6 = 0.\)

Chọn  A.

Phương pháp giải:

Bước 1: Chứng minh \(O,A\) nằm cùng phía so với \(\Delta \)

Bước 2: Tìm \(O'\) đối xứng \(O\) qua \(\Delta \)

Bước 3: Nhận xét để \(OM + MA\) nhỏ nhất thì \(O'AM\) thẳng hàng và tìm \(M = OA' \cap \Delta \)

Lời giải chi tiết:

\(\Delta \left( O \right).\Delta \left( A \right) = \left( {2.0 - 0 + 1} \right).\left( {2.2 - 1 + 1} \right) = 1.4 > 0\)

Suy ra \(O,A\) cùng phía so với \(\Delta \)

\(d\left\{ \begin{array}{l}qua\,O\left( {0;0} \right)\\ \bot \Delta \end{array} \right. \Rightarrow d:x + 2y = 0\)\( \Rightarrow H = d \cap \Delta  \Rightarrow H\left( {\frac{{ - 2}}{5};\frac{1}{5}} \right)\)

\(H\) là trung điểm \(OO' \Rightarrow \left\{ \begin{array}{l}{x_{O'}} = \frac{{ - 2}}{5}.2 - 0 = \frac{{ - 4}}{5}\\{y_{O'}} = \frac{1}{5}.2 - 0 = \frac{2}{5}\end{array} \right. \Rightarrow O'\left( {\frac{{ - 4}}{5};\frac{2}{5}} \right)\)

\(\left( {OM + MA} \right)\min  = \left( {O'M + MA} \right)\min \)

\( \Rightarrow O'MA\) thẳng hàng \( \Leftrightarrow O'A \cap \Delta  = M\)

\(\begin{array}{l}O'A\left\{ \begin{array}{l}qua\,\,A\left( {2;1} \right)\\VTPT\,\overrightarrow n  \bot \overrightarrow {O'A}  = \left( {\frac{{14}}{5};\frac{3}{5}} \right)\end{array} \right.\\ \Rightarrow 3\left( {x - 2} \right) - 14\left( {y - 1} \right) = 0 \Leftrightarrow 3x - 14y + 8 = 0\end{array}\)

\(M = O'A \cap \Delta  \Rightarrow M\left\{ \begin{array}{l}3x - 14y + 8 = 0\\2x - y + 1 = 0\end{array} \right. \Rightarrow M\left( {\frac{{ - 6}}{{25}};\frac{{13}}{{25}}} \right)\)

Chọn  C.

Phương pháp giải:

Để \(d\) cắt \(AB\) thì \(A,B\) khác phía so với \(d\) hoặc \(A \in d\)hoặc \(B \in d \Leftrightarrow \left( {a{x_A} + b{y_A} + c} \right)\left( {a{x_B} + b{y_B} + c} \right) \le 0\)

Lời giải chi tiết:

 Để \(d\) cắt \(AB\) thì

\(\begin{array}{l}\left( {{x_A} - {y_A} + 3} \right)\left( {{x_B} - {y_B} + 3} \right) \le 0 \Leftrightarrow \left( {1 - 2 + 3} \right)\left( {2 - m + 3} \right) \le 0\\ \Leftrightarrow 2.\left( {5 - m} \right) \le 0 \Leftrightarrow 5 - m \le 0 \Leftrightarrow m \ge 5\end{array}\)

Chọn  B.

Phương pháp giải:

Đưa phương trình đường thẳng \(d\) về dạng tổng quát. Sử dụng công thức khoảng cách từ điểm \(M\left( {{x_0};{y_0}} \right)\) đến đường thẳng \(\Delta :ax + by + c = 0\): \(d\left( {M;\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

Lời giải chi tiết:

\(d:\left\{ \begin{array}{l}qua\,\,A\left( {2; - 1} \right)\\\overrightarrow {{u_d}}  = \left( {1; - 2} \right) \Rightarrow \overrightarrow {{n_d}}  = \left( {2;1} \right)\end{array} \right. \Rightarrow d:2\left( {x - 2} \right) + \left( {y + 1} \right) = 0 \Leftrightarrow 2x + y - 3 = 0\)

\(d\left( {M;d} \right) = \frac{{\left| {2.0 + 1 - 3} \right|}}{{\sqrt {{2^2} + {1^2}} }} = \frac{2}{{\sqrt 5 }}\)

Chọn  C.

Phương pháp giải:

Sử dụng công thức khoảng cách từ điểm \(M\left( {{x_0};{y_0}} \right)\) đến đường thẳng \(\Delta :ax + by + c = 0\)  \(d\left( {M;\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

Lời giải chi tiết:

Sử dụng công thức khoảng cách từ điểm \(M\left( {{x_0};{y_0}} \right)\) đến đường thẳng \(\Delta :ax + by + c = 0\)  \(d\left( {M;\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

Chọn  A.

Phương pháp giải:

Sử dụng công thức khoảng cách từ điểm \(M\left( {{x_0};{y_0}} \right)\) đến đường thẳng \(\Delta :ax + by + c = 0\)  \(d\left( {M;\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

Lời giải chi tiết:

\(d\left( {M;d} \right) = \frac{{\left| {3.2 + 2.2 + 3} \right|}}{{\sqrt {{3^2} + {2^2}} }} = \sqrt {13} \)

Chọn  B.

Phương pháp giải:

Viết phương trình đường thẳng \(AD\) rồi tham số hóa điểm \(D\). Tính \(AD\) được từ diện tích \(ABCD\)

Lời giải chi tiết:

\(\overrightarrow {IM}  = \left( { - 1; - 2} \right) \Rightarrow IM = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}}  = \sqrt 5  \Rightarrow AB = 2IM = 2\sqrt 5 \)

\(S = 10 \Rightarrow AB.AD = 10 \Leftrightarrow 2\sqrt 5 .AD = 10 \Rightarrow AD = \sqrt 5 \)

\(AD:\left\{ \begin{array}{l}qua\,M\left( {0; - 1} \right)\\ \bot \overrightarrow {IM}  = \left( { - 1; - 2} \right) \Rightarrow \overrightarrow {{n_{AD}}}  = \left( {1;2} \right)\end{array} \right. \Rightarrow AD:\,x + 2y + 2 = 0\)

\( \Rightarrow D\left( { - 2t - 2;t} \right) \Rightarrow A = 2M - D = \left( {2t + 2; - 2 - t} \right)\)

\(\begin{array}{l}\overrightarrow {DA}  = \left( {4t + 4; - 2 - 2t} \right) \Rightarrow D{A^2} = {\left( {4t + 4} \right)^2} + {\left( { - 2 - 2t} \right)^2} = 5\\ \Leftrightarrow 20{t^2} + 40t + 15 = 0 \Rightarrow \left[ \begin{array}{l}t = \frac{{ - 1}}{2} \Rightarrow D\left( { - 1;\frac{{ - 1}}{2}} \right)\\t = \frac{{ - 3}}{2} \Rightarrow D\left( {1;\frac{{ - 3}}{2}} \right)\end{array} \right.\end{array}\)

Chọn  B.

Phương pháp giải:

Giả sử tọa độ tâm \(I\left( {a;b} \right)\) và sử dụng tính chất \(\left\{ \begin{array}{l}AI \bot BI \Rightarrow \overrightarrow {AI} .\overrightarrow {BI}  = 0\\AI = BI \Rightarrow A{I^2} = B{I^2}\end{array} \right.\)

Lời giải chi tiết:

Giả sử tọa độ tâm \(I\left( {a;b} \right)\)

\(\overrightarrow {AI}  = \left( {a - 3;b - 1} \right);\,\,\overrightarrow {BI}  = \left( {a;b - 2} \right)\)

Vì \(ABCD\) là hình vuông \( \Rightarrow \left\{ \begin{array}{l}AI \bot BI \Rightarrow \overrightarrow {AI} .\overrightarrow {BI}  = 0\\AI = BI \Rightarrow A{I^2} = B{I^2}\end{array} \right.\)

\( \Rightarrow \left\{ \begin{array}{l}\left( {a - 3} \right).a + \left( {b - 1} \right)\left( {b - 2} \right) = 0\\{\left( {a - 3} \right)^2} + {\left( {b - 1} \right)^2} = {a^2} + {\left( {b - 2} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a^2} - 3a + {b^2} - 3b + 2 = 0\\ - 6a + 2b + 6 = 0\end{array} \right.\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{a^2} - 3a + {b^2} - 3b + 2 = 0\\b = 3a - 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{a^2} - 3a + {\left( {3a - 3} \right)^2} - 3\left( {3a - 3} \right) + 2 = 0\\b = 3a - 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}10{a^2} - 30a + 20 = 0\\b = 3a - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}a = 1\\a = 2\end{array} \right.\\b = 3a - 3\end{array} \right. \Rightarrow \left[ \begin{array}{l}I\left( {1;0} \right)\\I\left( {2;3} \right)\end{array} \right.\end{array}\)

Chọn  D.

Phương pháp giải:

Tìm \(B\) bằng cách tìm giao của 2 đường thẳng \(AB,\,\,BD\). Muốn vậy phải viết phương trình đường thẳng \(BD\) dựa vào phân giác \(AC\) của \(\angle BAD\)

Lời giải chi tiết:

Phân giác \(AC\) của \(\angle BAD\) có pt \(\frac{{3x - y + 2}}{{\sqrt {{3^2} + {{\left( { - 1} \right)}^2}} }} =  \pm \frac{{x - 3y + 4}}{{\sqrt {{1^2} + {{\left( { - 3} \right)}^2}} }}\)

\( \Rightarrow \left[ \begin{array}{l}3x - y + 2 = x - 3y + 4\\3x - y + 2 =  - x + 3y - 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x + 2y - 2 = 0\\4x - 4y + 6 = 0\end{array} \right.\)

+ TH1: Nếu phương trình \(AC:2x + 2y - 2 = 0\)

Vì \( \Rightarrow BD\left\{ \begin{array}{l}qua\,M\left( {1;1} \right)\\ \bot AC \Rightarrow \overrightarrow {{n_{BD}}}  = \left( {1; - 1} \right)\end{array} \right. \Rightarrow BD:x - y = 0\)

\( \Rightarrow B = BD \cap AB = \left( { - 1; - 1} \right)\)

+ TH2: Nếu phương trình \(AC:4x - 4y + 6 = 0\)

Vì \( \Rightarrow BD\left\{ \begin{array}{l}qua\,M\left( {1;1} \right)\\ \bot AC \Rightarrow \overrightarrow {{n_{BD}}}  = \left( {1;1} \right)\end{array} \right. \Rightarrow BD:x + y - 2 = 0\)

\( \Rightarrow B = BD \cap AB = \left( {0;2} \right)\)

Chọn  D.

Phương pháp giải:

Nhận xét  tập hợp các điểm cách đường thẳng \(d\) với độ dài bằng \(2\) là đường thẳng \(d'\) song song với \(d\). Lấy \(M \in d\) và dùng công thức khoảng cách \(d\left( {M;d'} \right)\) tìm được \(d'\).

Lời giải chi tiết:

Tập hợp các điểm cách đường thẳng \(d\) với độ dài bằng \(2\) là  một đường thẳng song song với \(d\) có dạng \(d':3x + 4y + c = 0\)

\(\begin{array}{l}M\left( {2; - 1} \right) \in d \Rightarrow d\left( {M;d'} \right) = \frac{{\left| {3.2 + 4.\left( { - 1} \right) + c} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{{\left| {2 + c} \right|}}{5} = 2\\ \Rightarrow \left| {2 + c} \right| = 10 \Rightarrow \left[ \begin{array}{l}c = 8\\c =  - 12\end{array} \right. \Rightarrow \left[ \begin{array}{l}d':3x + 4y + 8 = 0\\d':3x + 4y - 12 = 0\end{array} \right.\end{array}\)

Chọn  C.

Phương pháp giải:

+ Xác định tọa độ điểm \(B\) (lấy \(I\) là trung điểm của \(AC\) \( \Rightarrow BI \bot AC\), \(B = d \cap BI\))

+ Viết phương trình đường thẳng \(AB,\,\,BC\).

Lời giải chi tiết:

Giả sử \(I\left( {{x_I};\,\,{y_I}} \right)\) là trung điểm của \(AC\)\( \Rightarrow \left\{ \begin{array}{l}{x_I} = \frac{{1 + 3}}{2} = 2\\{y_I} = \frac{{ - 1 + 5}}{2} = 2\end{array} \right. \Rightarrow I\left( {2;\,\,2} \right)\)

Vì tam giác \(ABC\) cân tại \(B\) nên \(BI \bot AC\). Phương trình đường thẳng \(BI\) đi qua \(I\left( {2;\,\,2} \right)\) nhận \(\overrightarrow {AC}  = \left( {2;6} \right)\) làm VTPT là:

\(2.\left( {x - 2} \right) + 6.\left( {y - 2} \right) = 0\)\( \Leftrightarrow 2x - 4 + 6y - 12 = 0\)

\( \Leftrightarrow 2x + 6y - 16 = 0\) \( \Leftrightarrow x + 3y - 8 = 0\)

Tọa độ giao điểm \(B\) của \(BI\) và \(d\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}2x - y = 0\\x + 3y - 8 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - y = 0\\x + 3y = 8\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = \frac{8}{7}\\y = \frac{{16}}{7}\end{array} \right. \Rightarrow B\left( {\frac{8}{7};\,\,\frac{{16}}{7}} \right)\)

+) \(A\left( {1;\, - 1} \right)\), \(B\left( {\frac{8}{7};\,\,\frac{{16}}{7}} \right)\)\( \Rightarrow \overrightarrow {AB}  = \left( {\frac{8}{7} - 1;\,\,\frac{{16}}{7} + 1} \right) = \left( {\frac{1}{7};\,\,\frac{{23}}{7}} \right)\)

Phương trình đường thẳng \(AB\) đi qua \(A\left( {1;\, - 1} \right)\) nhận \({\vec n_{AB}} = \left( {23;\,\, - 1} \right)\) làm VTPT là:

\(23.\left( {x - 1} \right) - 1.\left( {y + 1} \right) = 0\)\( \Leftrightarrow 23x - 23 - y - 1 = 0\) \( \Leftrightarrow 23x - y - 24 = 0\)

\( \Rightarrow a = 23;\,\,b =  - 1\)

+) \(B\left( {\frac{8}{7};\,\,\frac{{16}}{7}} \right)\), \(C\left( {3;\,\,5} \right)\)\( \Rightarrow \overrightarrow {BC}  = \left( {3 - \frac{8}{7};5 - \frac{{16}}{7}} \right) = \left( {\frac{{13}}{7};\,\,\frac{{19}}{7}} \right)\)

Phương trình đường thẳng \(BC\) đi qua \(C\left( {3;\,\,5} \right)\) nhận \({\vec n_{BC}} = \left( {19;\,\, - 13} \right)\) làm VTPT là:

\(19.\left( {x - 3} \right) + \left( { - 13} \right).\left( {y - 5} \right) = 0\)\( \Leftrightarrow 19x - 57 - 13y + 65 = 0\) \( \Leftrightarrow 19x - 13y + 8 = 0\)

\( \Rightarrow c = 19;\,\,d =  - 13\)

\( \Rightarrow a.b.c.d = 23.\left( { - 1} \right).19.\left( { - 13} \right) = 5681\)

Vậy \(a.b.c.d = 5681.\)

Chọn  B.

Phương pháp giải:

Sử dụng công thức đường phân giác giữa 2 đường thẳng \({d_1}:{a_1}x + {b_1}y + {c_1} = 0;\,\,{d_2}:{a_2}x + {b_2}y + {c_2} = 0\) là

\(\frac{{{a_1}x + {b_1}y + {c_1}}}{{\sqrt {a_1^2 + b_1^2} }} =  \pm \frac{{{a_2}x + {b_2}y + {c_2}}}{{\sqrt {a_2^2 + b_2^2} }}\)

Lời giải chi tiết:

Phương trình 2 đường phân giác: \(\frac{{2x + y + 1}}{{\sqrt {{2^2} + {1^2}} }} =  \pm \frac{{2x - 4y - 3}}{{\sqrt {{2^2} + {{\left( { - 4} \right)}^2}} }}\)

\(\frac{{2x + y + 1}}{{\sqrt 5 }} =  \pm \frac{{2x - 4y - 3}}{{2\sqrt 5 }} \Leftrightarrow \left[ \begin{array}{l}4x + 2y + 2 = 2x - 4y - 3\\4x + 2y + 2 =  - 2x + 4y + 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x + 6y + 5 = 0\\6x - 2y - 1 = 0\end{array} \right.\)

Chọn  B.

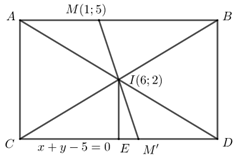
Phương pháp giải:

+ \(D \in BD:y = 2\) và điểm \(B\left( {1;2} \right)\)

+ \(BH = d\left( {B,\,\,CD} \right) = d\left( {B,\,\,\Delta } \right)\)

Lời giải chi tiết:

+) Gọi \(H\)  là hình chiếu vuông góc của \(B\)  trên \(CD\),  khi đó \(ABHD\)  là hình vuông.

Suy ra \(\angle CBH = \angle MBA\) (hai góc cùng phụ với \(\angle MBH\))

Từ đây ta có được \(\Delta CBH = \Delta MBA\) (g.c.g) \( \Rightarrow CB = MB \Rightarrow \Delta CBN = \Delta MBN\) (c.g.c)

Khi đó \(BH = d\left( {B,CN} \right) = d\left( {B,MN} \right) = \frac{{\left| {7 - 2 - 25} \right|}}{{\sqrt {50} }} = \frac{4}{{\sqrt 2 }} = 2\sqrt 2 .\)

Mà tam giác \(DHB\)  vuông cân tại \(H\) nên \(BD = \sqrt 2 BH = 4\)

+) Gọi \(D\left( {t;2} \right) \in BD\) với \(t > 0\), khi đó: \(B{D^2} = 16 \Leftrightarrow {\left( {t - 1} \right)^2} = 16 \Leftrightarrow t = 5\) hoặc \(t =  - 3\) (loại) \( \Rightarrow D\left( {5;2} \right)\)

Vậy \(D\left( {5;2} \right)\).

Chọn  D.

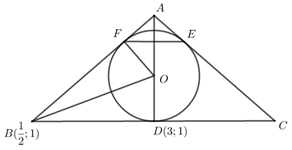
Phương pháp giải:

+ Lấy điểm \(M'\) đối xứng với \(M\) qua \(I.\) Xác định tọa độ điểm \(M'\).

+ \(IE \bot EM'\). Để xác định điểm \(E\) từ CT \(\overrightarrow {IE} \,.\,\overrightarrow {EM'}  = 0\).

Lời giải chi tiết:

Gọi \(M'\left( {{x_{M'}};\,\,{y_{M'}}} \right)\) là điểm đối xứng với \(M\left( {1;\,\,5} \right)\) qua \(I\left( {6;\,\,2} \right)\)\( \Rightarrow I\)là trung điểm của \(MM'.\)

Ta có: \(\left\{ \begin{array}{l}6 = \frac{{1 + {x_{M'}}}}{2}\\2 = \frac{{5 + {y_{M'}}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 + {x_{M'}} = 12\\5 + {y_{M'}} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{M'}} = 11\\{y_{M'}} =  - 1\end{array} \right. \Rightarrow M'\left( {11;\,\, - 1} \right)\)

Vì \(E \in \left( {CD} \right):\,\,x + y - 5 = 0 \Rightarrow E\left( {t;\,\,5 - t} \right)\)

Ta có:

+)\(E\left( {t;\,\,5 - t} \right)\); \(I\left( {6;\,\,2} \right)\)\( \Rightarrow \overrightarrow {IE}  = \left( {t - 6;\,\,3 - t} \right)\)

+) \(E\left( {t;\,\,5 - t} \right);\,\,M'\left( {11;\,\, - 1} \right) \Rightarrow \overrightarrow {EM'}  = \left( {11 - t;\,\, - 6 + t} \right)\)

\(ABCD\) là hình chữ nhật, \(I\) là giao điểm hai đường chéo, \(E\) là trung điểm của \(CD\)\( \Rightarrow IE \bot CD\)\( \Rightarrow IE \bot EM'\)

\( \Rightarrow \overrightarrow {IE} \,.\,\,\overrightarrow {EM'}  = 0\)

\( \Rightarrow \left( {t - 6} \right).\left( {11 - t} \right) + \left( {3 - t} \right).\left( { - 6 + t} \right) = 0\)

\( \Leftrightarrow 11t - {t^2} + 6t - 66 - 18 + 3t + 6t - {t^2} = 0\)

\( \Leftrightarrow  - 2{t^2} + 26t - 84 = 0\)\( \Leftrightarrow {t^2} - 13t - 42 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 6\\t = 7\end{array} \right.\)\( \Rightarrow E\left( {6;\,\, - 1} \right)\) và \(E\left( {7;\,\, - 2} \right)\)

Chọn  A

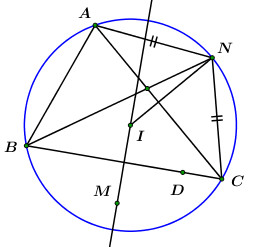
Phương pháp giải:

+) Chứng minh tam giác \(ABC\) cân tại \(A\).

+) \(A = AD \cap BF\).

Lời giải chi tiết:

*) \(\left( {{\rm{EF}}} \right):\,\,y - 2 = 0 \Rightarrow {\vec n_{{\rm{EF}}}} = \left( {0;\,\,1} \right) \Rightarrow {\vec u_{{\rm{EF}}}} = \left( {1;\,\,0} \right)\)

Ta có: \(B\left( {\frac{1}{2};\,\,1} \right),\,\,D\left( {3;\,\,1} \right) \Rightarrow \overrightarrow {BD}  = \left( {\frac{5}{2};\,\,0} \right) \Rightarrow {\vec u_{BD}} = \left( {1;\,\,0} \right)\)

\( \Rightarrow EF\,{\rm{//}}\,BD\)\( \Rightarrow EF\,{\rm{//}}\,BD \Rightarrow \Delta ABC\) cân tại \(A\).

*) Lập phương trình đường thẳng \(AD\)

Ta có:

+ \(AD\) là đường phân giác trong góc \(A\) nên \(AD \bot BC\)

+ \(\Delta ABC\) cân tại \(A\)

\( \Rightarrow AD \bot BC\)

\(\left( {AD} \right):\,\,\left\{ \begin{array}{l}{\rm{qua}}\,\,D\left( {3;\,\,1} \right)\\{{\vec n}_{AD}} = {{\vec u}_{BD}} = \left( {1;\,\,0} \right)\end{array} \right.\)\( \Rightarrow 1.\left( {x - 3} \right) + 0.\left( {y - 1} \right) = 0 \Leftrightarrow x - 3 = 0\)

*) Lập phương trình đường thẳng \(BF.\)

Gọi \(F\left( {t;\,\,3} \right) \Rightarrow \overrightarrow {BF}  = \left( {t - \frac{1}{2};\,\,2} \right)\)

Ta có: \(BD = BF \Rightarrow \sqrt {{{\left( {\frac{5}{2}} \right)}^2}}  = \sqrt {{{\left( {t - \frac{1}{2}} \right)}^2} + {2^2}}  \Leftrightarrow \frac{{25}}{4} = {\left( {t - \frac{1}{2}} \right)^2} + {2^2} \Leftrightarrow \left[ \begin{array}{l}t =  - 1\\t = 2\end{array} \right.\)

+) Với \(t =  - 1 \Rightarrow F\left( { - 1;\,\,3} \right),\,\,\overrightarrow {BF}  = \left( { - \frac{3}{2};\,\,2} \right)\).

\(\left( {BF} \right):\left\{ \begin{array}{l}{\rm{qua}}\,F\left( { - 1;\,\,3} \right)\\{{\vec n}_{BF}} = \left( {2;\,\,\frac{3}{2}} \right)\end{array} \right. \Rightarrow 2.\left( {x + 1} \right) + \frac{3}{2} \cdot \left( {y - 3} \right) = 0 \Leftrightarrow 2x + 2 + \frac{3}{2}y - \frac{9}{2} = 0 \Leftrightarrow 4x + 3y - 5 = 0\)

Ta có: \(A = AD \cap BF\)

Tọa độ giao điểm \(A\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}x - 3 = 0\\4x + 3y - 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y =  - \frac{7}{3}\end{array} \right. \Rightarrow A\left( {3;\,\, - \frac{7}{3}} \right)\) (loại)

+) Với \(t = 2 \Rightarrow F\left( {2;\,\,3} \right)\), \(\overrightarrow {BF}  = \left( { - \frac{3}{2};\,\,2} \right)\).

\(\left( {BF} \right):\left\{ \begin{array}{l}{\rm{qua}}\,F\left( {2;\,\,3} \right)\\{{\vec n}_{BF}} = \left( {2;\,\, - \frac{3}{2}} \right)\end{array} \right. \Rightarrow 2.\left( {x - 2} \right) - \frac{3}{2} \cdot \left( {y - 3} \right) = 0 \Leftrightarrow 2x - 4 - \frac{3}{2}y + \frac{9}{2} = 0 \Leftrightarrow 4x - 3y + 1 = 0\)

Ta có: \(A = AD \cap BF\)

Tọa độ giao điểm \(A\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}4x - 3y + 1 = 0\\x - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = \frac{{13}}{3}\end{array} \right. \Rightarrow A\left( {3;\,\,\frac{{13}}{3}} \right)\) (thỏa mãn)

Vậy \(A\left( {3;\,\,\frac{{13}}{3}} \right) \cdot \)

Chọn B

Phương pháp giải:

+) Viết phương trình đường tròn ngoại tiếp tam giác \(ABC\).

+) Viết phương trình đường thẳng \(BC\)\( \Rightarrow \) Tọa độ của \(B,\,\,C\).

+) \(AC\) đi qua \(C\) và vuông góc với \(IN\)\( \Rightarrow \) Xác định tọa độ đỉnh \(A\).

Lời giải chi tiết:

Gọi \(\left( C \right)\) là đường tròn ngoại tiếp \(\Delta ABC\).

Do \(NA = NC\) nên \(N\) nằm trên đường trung trực của \(AC\).

\(\left\{ \begin{array}{l}\angle AIC = 2\angle ABC\\\angle AIC = 2\angle NIC\end{array} \right. \Rightarrow \angle NIC = \angle ABC = 2\angle NBC \Rightarrow N \in \left( C \right)\).

Đường tròn \(\left( C \right)\) có tâm \(I\left( { - 1;\,\,0} \right)\) và bán kính \(R = IN\) \( = \sqrt {{3^2} + {4^2}}  = 5\) có phương trình \(\left( C \right):{\left( {x + 1} \right)^2} + {y^2} + 25\). Đường thẳng \(BC\) đi qua \(D\left( {1;\,\,4} \right)\) có VTPT  là \(\overrightarrow {IM}  = (4;3)\) có phương trình \(BC:4x + 3y - 16 = 0\).

Điểm \(B,\,\,C\) là giao điểm của \(BC\) và \(\left( C \right)\) nên tọa độ của \(B,\,\,C\) là nghiệm của hệ

\(\left\{ \begin{array}{l}{\left( {x + 1} \right)^2} + {y^2} = 25\\4x + 3y - 16 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 4\\y = 0\end{array} \right.\\\left\{ \begin{array}{l}x = \frac{2}{5}\\y = \frac{{24}}{5}\end{array} \right.\end{array} \right.\).

Do \({y_B} > {y_C}\) nên \(B\left( {\frac{2}{5};\frac{{24}}{5}} \right),C(4;0)\).

Ta có: \(AC\) đi qua \(C\) và vuông góc \(IN\) nên có phương trình \(AC:3x + 4y - 12 = 0\).

Điểm \(A\) là giao điểm của \(AC\) và \(\left( C \right)\) nên tọa độ của điểm \(A\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}{\left( {x + 1} \right)^2} + {y^2} = 25\\3x + 4y - 12 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 4\\y = 0\end{array} \right.\\\left\{ \begin{array}{l}x =  - \frac{{12}}{5}\\y = \frac{{24}}{5}\end{array} \right.\end{array} \right.\).

Loại \(\left\{ \begin{array}{l}x = 4\\y = 0\end{array} \right.\) vì trùng điểm \(C\).

Vậy \(A\left( { - \frac{{12}}{5};\frac{{24}}{5}} \right)\).

Tọa độ các điểm cần tìm là: \(A\left( { - \frac{{12}}{5};\frac{{24}}{5}} \right),\,\,B\left( {\frac{2}{5};\frac{{24}}{5}} \right),\,\,C(4;0)\).

Chọn  D.

Phương pháp giải:

+) Biểu diễn tọa độ của điểm \(B,\,\,C\) theo \(a\) hoặc \(b\).

+) \(\left. \begin{array}{l}B \in d\\HC \bot d = \left\{ H \right\}\end{array} \right\} \Rightarrow BH \bot HC \Leftrightarrow \overrightarrow {BH} .\overrightarrow {HC}  = 0\)

Lời giải chi tiết:

+) Vì \(B\left( {a;\,\,b} \right)\) nằm trên đường thẳng \(d:\,\,x + y + 2 = 0\) nên ta có: \(a + b + 2 = 0 \Rightarrow b =  - a - 2\)

\( \Rightarrow B\left( {a;\,\, - a - 2} \right)\)

+) Ta có: \(A\left( {2;\,\,4} \right),\,\,B\left( {a;\,\, - a - 2} \right),\,\,C\left( {{x_C};\,\,{y_C}} \right)\)

Vì \(G\left( {2;\,\,\frac{2}{3}} \right)\) là trọng tâm tam giác \(ABC\) nên  \(\left\{ \begin{array}{l}2 = \frac{{2 + a + {x_C}}}{3}\\\frac{2}{3} = \frac{{4 + \left( { - a - 2} \right) + {y_C}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2 + a + {x_C} = 6\\2 - a + {y_C} = 2\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}a + {x_C} = 4\\ - a + {y_C} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 4 - a\\{y_C} = a\end{array} \right.\)

\( \Rightarrow C\left( {4 - a;\,\,a} \right)\)

+) \(\overrightarrow {HB}  = \left( {a - 2;\,\, - a + 2} \right)\), \(\overrightarrow {HC}  = \left( {2 - a;\,\,a + 4} \right)\)

Vì \(B\left( {a;\,\, - a - 2} \right) \in d\) và \(H\left( {2;\,\, - 4} \right)\) là hình chiếu của \(C\left( {4 - a;\,\,a} \right)\) lên đường thẳng \(d\), khi đó ta có:

\(\overrightarrow {HB.} \overrightarrow {HC}  = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\) 

\( \Rightarrow \left( {a - 2} \right)\left( {2 - a} \right) + \left( { - a + 2} \right)\left( {a + 4} \right) = 0\)

\( \Leftrightarrow \left( {a - 2} \right)\left( {2 - a} \right) + \left( {2 - a} \right)\left( {a + 4} \right) = 0\)

\( \Leftrightarrow \left( {2 - a} \right)\left[ {\left( {a - 2} \right) + \left( {a + 4} \right)} \right] = 0\)

\( \Leftrightarrow \left( {2 - a} \right)\left( {2a + 2} \right) = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}2 - a = 0\\2a + 2 = 0\end{array} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}a = 2\\a =  - 1\end{array} \right.\)

- Với \(a = 2 \Rightarrow B\left( {2;\,\, - 4} \right),\,\,C\left( {2;\,\,2} \right)\), \(A\left( {2;\,\,4} \right)\)\( \Rightarrow \) Ba điểm \(A,\,\,B,\,\,C\) thẳng hàng \( \Rightarrow \) Loại

- Với \(a =  - 1 \Rightarrow \)\(B\left( { - 1;\,\, - 1} \right),\,\,C\left( {5;\,\, - 1} \right)\)

\( \Rightarrow P = a - 3b = \left( { - 1} \right) - 3.\left( { - 1} \right) = 2\)

Chọn  C.

Phương pháp giải:

Biến đổi hệ BPT và biện luận.

Lời giải chi tiết:

Gọi G là trọng tâm tam giác ABC \( \Rightarrow G\left( { - 1;\frac{4}{3}} \right)\)

\( \Rightarrow \left| {\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC} } \right| = \left| {3\overrightarrow {MG} } \right| = 3MG\)

Để \(\left| {\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC} } \right|\) nhỏ nhất \( \Leftrightarrow MG\) nhỏ nhất \( \Leftrightarrow \) M là hình chiếu của G trên d

Gọi \(d'\) là đường thẳng qua G vuông góc với d \( \Rightarrow d \cap d' = \left\{ M \right\}\)

d nhận \(\overrightarrow n  = \left( {2; - 1} \right)\) là VTPT \( \Rightarrow \overrightarrow {n'}  = \left( {1;2} \right)\) là VTPT của \(d'\)

\( \Rightarrow \) Phương trình \(d':\left( {x + 1} \right) + 2\left( {y - \frac{4}{3}} \right) = 0 \Leftrightarrow x + 2y - \frac{5}{3} = 0\)

Tọa độ điểm M là nghiệm của hệ : \(\left\{ \begin{array}{l}2x - y + 3 = 0\\x + 2y - \frac{5}{3} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - \frac{{13}}{{15}} = a\\y = \frac{{19}}{{15}} = b\end{array} \right.\)

\( \Rightarrow 5\left( {a + b} \right) = 5\left( { - \frac{{13}}{{15}} + \frac{{19}}{{15}}} \right) = 2\) 

Chọn C.

Phương pháp giải:

Ta có: \(M \in Oy \Rightarrow M\left( {0;\,\,m} \right).\)

 Ta có: \(\left| {MA - MB} \right| \le AB.\)

\( \Rightarrow Max\left| {MA - MB} \right| = AB \Leftrightarrow A,\,\,B,\,\,M\,\,\)thẳng hàng.

Lời giải chi tiết:

Ta có: \(M \in Oy \Rightarrow M\left( {0;\,\,m} \right) \Rightarrow \left\{ \begin{array}{l}\overrightarrow {MA}  = \left( {1;\,\,1 - m} \right)\\\overrightarrow {AB}  = \left( {2;\,\,3} \right)\end{array} \right.\)

 Ta có: \(\left| {MA - MB} \right| \le AB.\)

\( \Rightarrow Max\left| {MA - MB} \right| = AB \Leftrightarrow A,\,\,B,\,\,M\,\,\)thẳng hàng.

\( \Rightarrow \overrightarrow {MA}  = k\overrightarrow {AB}  \Leftrightarrow \left( {1;\,\,1 - m} \right) = k\left( {2;\,\,3} \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}1 = 2k\\1 - m = 3k\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k = \frac{1}{2}\\m =  - \frac{1}{2}\end{array} \right. \Rightarrow M\left( {0; - \frac{1}{2}} \right).\)

Chọn  B.

Phương pháp giải:

Lập phương trình đường thẳng \(AC\) đi qua \(A\) và vuông góc với \(BH.\) 

Từ đó ta tìm được tọa độ điểm \(C\) là giao điểm của\(AC\) và  \(CD.\)

Gọi \(K\) là điểm đối xứng của \(H\) qua \(CD \Rightarrow \) tọa độ điểm \(K.\)

Lập phương trình đường thẳng \(BC\) đi qua \(K\) và \(C.\)

\( \Rightarrow B\) là giao điểm của \(BC\) và \(BH.\)

Lời giải chi tiết:

Ta có: \(\overrightarrow {{n_{BH}}}  = \left( {1;\, - 1} \right).\)

Đường thẳng \(AC\) đi qua \(A\) và vuông góc với \(BH \Rightarrow AC\) nhận  vecto \(\left( {1;\,\,1} \right)\) làm VTPT

\( \Rightarrow AC:\,\,x + 1 + y - 3 = 0 \Leftrightarrow x + y - 2 = 0.\)

Khi đó tọa độ điểm \(C\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}x + 3y + 2 = 0\\x + y - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y =  - 2\end{array} \right. \Rightarrow C\left( {4; - 2} \right).\)

\(BH \cap AC = \left\{ H \right\} \Rightarrow \) tọa độ điểm \(H\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}x + y - 2 = 0\\x - y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 1\end{array} \right. \Rightarrow H\left( {1;\,\,1} \right).\)

Gọi \(K\) là điểm đối xứng của \(H\) qua \(CD\) 

Phương trình đường thẳng \(HK\) đi qua \(H\) và vuông góc với \(CD,\) nhận \(\left( {3; - 1} \right)\)  làm VTPT  là:

\(HK:\,\,\,3\left( {x - 1} \right) - \left( {y - 1} \right) = 0 \Leftrightarrow 3x - y - 2 = 0\)

Gọi \(I\) là giao điểm của \(CD\) và \(HK \Rightarrow \) tọa độ điểm \(I\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}x + 3y + 2 = 0\\3x - y - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{2}{5}\\y =  - \frac{4}{5}\end{array} \right. \Rightarrow I\left( {\frac{2}{5}; - \frac{4}{5}} \right).\)

\(K\) là điểm đối xứng của \(H\) qua \(CD \Rightarrow I\)  là trung điểm của \(HK \Rightarrow K\left( { - \frac{1}{5}; - \frac{{13}}{5}} \right)\)

Phương trình đường thẳng đi qua \(C\left( {4; - 2} \right)\) và \(K\left( { - \frac{1}{5}; - \frac{{13}}{5}} \right)\) là:

\(\begin{array}{l}\frac{{x - 4}}{{ - \frac{1}{5} - 4}} = \frac{{y + 2}}{{ - \frac{{13}}{5} + 2}} \Leftrightarrow \frac{3}{5}\left( {x - 4} \right) = \frac{{21}}{5}\left( {y + 2} \right)\\ \Leftrightarrow x - 4 = 7y + 14 \Leftrightarrow x - 7y - 18 = 0\end{array}\)

Khi đó \(B\) là giao điểm của \(BH\) và \(BC \Rightarrow \) tọa độ điểm \(B\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}x - y = 0\\x - 7y - 18 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 3\\y =  - 3\end{array} \right. \Rightarrow B\left( { - 3; - 3} \right).\)

Chọn  B.

Phương pháp giải:

B1: Tìm tọa độ giao điểm \(M\)  của \({d_1},\,\,{d_3}.\)

B2: Để \({d_1},\,\,{d_2}\) cắt nhau tại một điểm thuộc \({d_3}\) thì \(M \in {d_2}.\) Thay tọa độ điểm \(M\) vào phương trình của  \({d_2}\) để tìm \(m.\) 

B3: Kiểm tra lại giá trị \(m\) vừa tìm được xem hai đường thẳng \({d_1},\,\,{d_2},\,\,{d_3}\) có  trùng nhau không rồi kết luận.

Lời giải chi tiết:

Gọi \(M\) là giao điểm của \({d_1},\,\,{d_3}.\) Khi đó tọa độ của điểm \(M\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}x - 2y + 1 = 0\\x + y - 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 2\end{array} \right. \Rightarrow M\left( {3;\,\,2} \right).\)

Để \({d_1},\,\,{d_2}\) cắt nhau tại một điểm thuộc \({d_3}\) thì \(M \in {d_2}.\)

\(\begin{array}{l} \Rightarrow 3m - \left( {3m - 2} \right).2 + 2m - 2 = 0\\ \Leftrightarrow 3m - 6m + 4 + 2m - 2 = 0\\ \Leftrightarrow m = 2.\end{array}\)

Thay \(m = 2\) vào phương trình đường thẳng \({d_2}\) ta được: \({d_2}:\,\,2x - 4y + 2 = 0 \Leftrightarrow x - 2y + 1 = 0.\)

Ta thấy \({d_1} \equiv {d_2} \Rightarrow m = 2\) không thỏa mãn.

Vậy không có giá trị của \(m\) thỏa mãn bài toán.

Chọn  D

Phương pháp giải:

Gọi \(H\) là hình chiếu của \(I\) trên \(AB\)và tính \(IH \Rightarrow AH \Rightarrow A\)

Lời giải chi tiết:

Gọi \(H\) là hình chiếu của \(I\) trên \(AB\)

\(IH = d\left( {I;AB} \right) = \frac{{\left| 2 \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \sqrt 2 \)

\(Pt\,\,IH:\left\{ \begin{array}{l}qua\,\,I\left( {0;0} \right)\\ \bot AB:x - y + 2 = 0\end{array} \right. \Rightarrow IH:x + y = 0\)

\(H = AB \cap IH \Rightarrow H:\left\{ \begin{array}{l}x - y + 2 = 0\\x + y = 0\end{array} \right. \Rightarrow H\left( { - 1;1} \right)\)

Vì \(A \in AB \Rightarrow A\left( {t;t + 2} \right)\,\,\left( {t > 0} \right)\)

\(AB = 2AD \Rightarrow AH = 2d\left( {I;AB} \right) = 2\sqrt 2 \)

\(\begin{array}{l} \Rightarrow A{H^2} = {\left( {2\sqrt 2 } \right)^2} \Leftrightarrow {\left( {t + 1} \right)^2} + {\left( {t + 1} \right)^2} = 8 \Rightarrow {\left( {t + 1} \right)^2} = 4\\ \Rightarrow \left[ \begin{array}{l}t = 1\,\,\,\left( {tm} \right)\\t =  - 3\,\,\left( {ktm} \right)\end{array} \right. \Rightarrow A\left( {1;3} \right)\end{array}\)

Chọn  B.

Phương pháp giải:

Tìm điểm I thỏa mãn \(2\overrightarrow {IA}  + \overrightarrow {IB}  = \overrightarrow 0 \) từ đó suy ra \(2A{M^2} + M{B^2}\) nhỏ nhất khi IM nhỏ nhất\( \Leftrightarrow \) M là hình chiếu vuông góc của I lên \(\Delta \) từ đó tìm M

Lời giải chi tiết:

Gọi điểm \(I\left( {a;b} \right)\) thỏa mãn \(2\overrightarrow {IA}  + \overrightarrow {IB}  = \overrightarrow 0  \Leftrightarrow 2\left( { - 1 - a;\;2 - b} \right) + \left( {3 - a;\;4 - b} \right) = \overrightarrow 0 \)

\( \Rightarrow \left\{ \begin{array}{l}2\left( { - 1 - a} \right) + 3 - a = 0\\2\left( {2 - b} \right) + 4 - b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 3a + 1 = 0\\ - 3b + 8 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{3}\\b = \frac{8}{3}\end{array} \right. \Rightarrow I\left( {\frac{1}{3};\frac{8}{3}} \right).\)

Ta có: \(2A{M^2} + M{B^2} = 2{\left( {\overrightarrow {IM}  - \overrightarrow {IA} } \right)^2} + {\left( {\overrightarrow {IB}  - \overrightarrow {IM} } \right)^2}\)

      \(\begin{array}{l} = 2\left( {I{M^2} - 2\overrightarrow {IM} .\overrightarrow {IA}  + I{A^2}} \right) + I{B^2} - 2\overrightarrow {IB} .\overrightarrow {IM}  + I{M^2}\\ = 3I{M^2} + 2I{A^2} + I{B^2} - 2\overrightarrow {IM} \left( {2\overrightarrow {IA}  + \overrightarrow {IB} } \right) = 3I{M^2} + 2I{A^2} + I{B^2}\end{array}\)

\(2I{A^2} + I{B^2}\) không thay đổi nên \(2A{M^2} + M{B^2}\) nhỏ nhất khi IM  nhỏ nhất

\( \Leftrightarrow \) M là hình chiếu vuông góc của I  lên \(\Delta \)

 \(\Delta \) có VTPT là \(\overrightarrow n  = \left( {1; - 2} \right)\)

Gọi d  là đường thẳng đi qua I  vuông góc với \(\Delta \)

\( \Rightarrow \) d  nhận \(\overrightarrow {{n_1}}  = \left( {2;\;1} \right)\) làm VTPT

\( \Rightarrow \)Phương trình tổng quát của d  là: \(2\left( {x - \frac{1}{3}} \right) + \left( {y - \frac{8}{3}} \right) = 0 \Leftrightarrow 2x + y - \frac{{10}}{3} = 0\)

M  là giao điểm của d và \(\Delta \)\( \Rightarrow \) tọa độ điểm M  là nghiệm của hệ phương trình:

 \(\left\{ \begin{array}{l}2x + y - \frac{{10}}{3} = 0\\x - 2y - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{26}}{{15}}\\y =  - \frac{2}{{15}}\end{array} \right. \Rightarrow M\left( {\frac{{26}}{{15}}; - \frac{2}{{15}}} \right).\)

Vậy \(M\left( {\frac{{26}}{{15}}; - \frac{2}{{15}}} \right)\) thỏa mãn yêu cầu đề bài.

Chọn A.

Phương pháp giải:

Gọi phương trình d cần tìm theo đoạn chắn.

Lời giải chi tiết:

Ta có A, B là giao điểm của d với hai tia Ox,Oy nên gọi \(A\left( {a;\;0} \right);\;B\left( {0;\;b} \right)\;\;\;\left( {a > 2;\;b > 1} \right).\) 

\( \Rightarrow \) Phương trình d  theo đoạn chắn là: \(\frac{x}{a} + \frac{y}{b} = 1\)

Do  \(M \in d \Rightarrow \frac{2}{a} + \frac{1}{b} = 1\;\;\;\;\left( 1 \right)\)     

Mặt khác: \({S_{OAB}} = \frac{1}{2}OA.OB = \frac{1}{2}\left| {ab} \right| = \frac{1}{2}ab\)

Để diện tích tam giác OAB là nhỏ nhất \( \Leftrightarrow ab\) nhỏ nhất

Ta có:  \(1 = \frac{2}{a} + \frac{1}{b} \ge 2\sqrt {\frac{2}{{ab}}}  \Leftrightarrow \frac{2}{{ab}} \le \frac{1}{4} \Leftrightarrow ab \ge 8\)

Vậy diện tích tam giác OAB là nhỏ nhất \( \Leftrightarrow ab = 8\;\;\;\;\left( 2 \right)\)   

Từ (1) và (2) ta có hệ: \(\left\{ \begin{array}{l}\frac{2}{a} + \frac{1}{b} = 1\\ab = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2b + a = ab = 8\\ab = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 8 - 2b\\\left( {8 - 2b} \right)b = 8\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}a = 8 - 2b\\2{b^2} - 8b + 8 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 4\\b = 2\end{array} \right.\,\,\,(tm)\)

\( \Rightarrow \) Phương trình d: \(\frac{x}{4} + \frac{y}{2} = 1 \Leftrightarrow x + 2y - 4 = 0\)

Chọn C.

Phương pháp giải:

Gọi \(\overrightarrow n  = \left( {a;b} \right)\) là một VTPT của \(\left( d \right)\). Viết phương trình \(\left( d \right)\). Tính khoảng cách từ \(A\) đến .

Áp dụng BĐT Binhiacopxki để tìm tỉ số \(\frac{a}{b}\) sao cho thỏa mãn yêu cầu đề bài.

Lời giải chi tiết:

Gọi \(\overrightarrow n  = \left( {a;b} \right)\) là một VTPT của \(\left( d \right)\).

\( \Rightarrow \) Phương trình : \(a\left( {x - 3} \right) + b\left( {y - 4} \right) = 0 \Leftrightarrow ax + by - 3a - 4b = 0\)

Khi đó: \(d\left( {A;\left( d \right)} \right) = \frac{{\left| {a - b - 3a - 4b} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \frac{{\left| {2a + 5b} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

Áp dụng BĐT Binhiacopxki \( \Rightarrow d\left( {A;\left( d \right)} \right) \le \frac{{\sqrt {\left( {4 + 25} \right)\left( {{a^2} + {b^2}} \right)} }}{{\sqrt {{a^2} + {b^2}} }} = \sqrt {29} \)

Dấu “=” xảy ra \( \Leftrightarrow \frac{a}{2} = \frac{b}{5} \Leftrightarrow \frac{a}{b} = \frac{2}{5}\)

Chọn \(a = 2;\,\,b = 5 \Rightarrow \)  Phương trình \(d:\,\,2x + 5y - 26 = 0\)

Chọn D.

Phương pháp giải:

Gọi M theo 1 chữ, từ diện tích \(\Delta MAB\) bằng 1 viết phương trình tìm M.

Lời giải chi tiết:

Gọi \(M\left( {0;m} \right) \in Oy;\,\,AB = \sqrt {{{\left( {4 - 1} \right)}^2} + {{\left( {6 - 2} \right)}^2}}  = 5.\) 

Có  \({S_{\Delta MAB}} = \frac{1}{2}d\left( {M,AB} \right).AB \Leftrightarrow 1 = \frac{1}{2}.d\left( {M,AB} \right).5 \Leftrightarrow d\left( {M,AB} \right) = \frac{2}{5}\)

\(\overrightarrow {AB}  = \left( {3;4} \right) \Rightarrow \overrightarrow n  = \left( {4; - 3} \right)\) là 1 VTPT của  AB.

\( \Rightarrow \) Phương trình AB: \(4\left( {x - 1} \right) - 3\left( {y - 2} \right) = 0 \Leftrightarrow 4x - 3y + 2 = 0\)

\( \Rightarrow d\left( {M,AB} \right) = \frac{{\left| { - 3m + 2} \right|}}{{\sqrt {{4^2} + {3^2}} }} \Leftrightarrow \frac{2}{5} = \frac{{\left| { - 3m + 2} \right|}}{5} \Leftrightarrow \left| { - 3m + 2} \right| = 2\)

\( \Leftrightarrow \left[ \begin{array}{l} - 3m + 2 = 2\\ - 3m + 2 =  - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0 \Rightarrow M\left( {0;0} \right)\\m = \frac{4}{3} \Rightarrow M\left( {0;\frac{4}{3}} \right)\end{array} \right.\) 

Chọn B.

Phương pháp giải:

+) \(CM\) là đường trung tuyến của \(\Delta ABC \Rightarrow M\) là trung điểm của \(AB.\)

+) Lập phương trình đường trung tuyến \(CM\) đi qua \(C,\,\,M.\) 

Lời giải chi tiết:

\(CM\) là đường trung tuyến của \(\Delta ABC \Rightarrow M\) là trung điểm của \(AB \Rightarrow \left\{ \begin{array}{l}{x_M} = \frac{{{x_A} + {x_B}}}{2} = 2\\{y_M} = \frac{{{y_M} + {y_B}}}{2} = 3\end{array} \right. \Rightarrow M\left( {2;\,3} \right).\)

\( \Rightarrow \overrightarrow {CM}  = \left( { - 5;\,0} \right) =  - 5\left( {1;\,\,0} \right)//\,\overrightarrow u  = \left( {1;\,0} \right).\)

\( \Rightarrow \) Phương trình đường thẳng \(CM\) đi qua \(M\left( {7;\,3} \right)\) và có VTCP  \(\overrightarrow u  = \left( {1;\,0} \right)\) là: \(\left\{ \begin{array}{l}x = 7 + t\\y = 3\end{array} \right..\)

Chọn  C.

Phương pháp giải:

\(ABCD\) là hình bình hành nên \(AB//CD.\)

\( \Rightarrow \) Đường thẳng \(AB\) đi qua \(A\) và nhận VTCP của đường thẳng \(CD\) làm VTCP.

Lời giải chi tiết:

Ta có: \(CD:\,\,\,\left\{ \begin{array}{l}x = 1 + 4t\\y = 3t\end{array} \right.\) nhận \(\overrightarrow u  = \left( {4;\,3} \right)\) làm VTCP.

\( \Rightarrow \) Đường thẳng \(AB\) đi qua \(A\) và nhận \(\overrightarrow u  = \left( {4;\,3} \right)\) làm VTCP\( \Rightarrow AB:\,\,\left\{ \begin{array}{l}x =  - 2 + 4t\\y = 1 + 3t\end{array} \right..\)

Ta có: \(\overrightarrow u  = \left( {4;3} \right)//\overrightarrow v  = \left( { - 4; - 3} \right)\)

\( \Rightarrow \) Đường thẳng \(AB\) đi qua \(A\) và nhận \(\overrightarrow v  = \left( { - 4; - \,3} \right)\) làm VTCP\( \Rightarrow AB:\,\,\left\{ \begin{array}{l}x =  - 2 - 4t\\y = 1 - 3t\end{array} \right..\)

Chọn  B.

Phương pháp giải:

Tìm tọa độ điểm A là giao điểm của \((\Delta )\)và \((d)\)

Tìm  N  là điểm sao cho ABNC là hình bình hành

Tìm điểm B là giao của BN và \(\Delta \)

Viết phương trình đường thẳng BM  là đường thẳng cần tìm

Lời giải chi tiết:

Gọi A là giao điểm của \((\Delta )\)và \((d)\)

\( \Rightarrow \) Tọa độ điểm A  là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}2x + y - 1 = 0\\3x + 7y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{8}{{11}}\\y =  - \frac{5}{{11}}\end{array} \right. \Rightarrow A\left( {\frac{8}{{11}}; - \frac{5}{{11}}} \right).\)

Gọi \(N\left( {a;\,\,b} \right)\)   là điểm sao cho ABNC là hình bình hành

\(\begin{array}{l} \Rightarrow \overrightarrow {AM}  = \overrightarrow {MN}  \Leftrightarrow \left( {a - 1;\,b - 1} \right) = \left( {1 - \frac{8}{{11}};\,1 + \frac{5}{{11}}} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}a - 1 = 1 - \frac{8}{{11}}\\b - 1 = 1 + \frac{5}{{11}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{14}}{{11}}\\b = \frac{{27}}{{11}}\end{array} \right. \Rightarrow N\left( {\frac{{14}}{{11}};\frac{{27}}{{11}}} \right)\end{array}\)

Đường thẳng \(\left( {BN} \right)\) là đường thẳng đi qua N và song song với \((d)\)

\( \Rightarrow \left( {BN} \right):3\left( {x - \frac{{14}}{{11}}} \right) + 7\left( {y - \frac{{27}}{{11}}} \right) = 0 \Leftrightarrow 3x + 7y - 21 = 0\)

B là giao điểm của \((\Delta )\)và \((BN) \Rightarrow \) tọa độ điểm \(B\) là nghiệm của hệ:\(\left\{ \begin{array}{l}2x + y - 1 = 0\\3x + 7y - 21 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - \frac{{14}}{{11}}\\y = \frac{{39}}{{11}}\end{array} \right. \Rightarrow B\left( { - \frac{{14}}{{11}};\frac{{39}}{{11}}} \right)\)

Phương trình đường thẳng \(\left( {BM} \right)\) cần tìm là: \(\frac{{x - 1}}{{ - \frac{{14}}{{11}} - 1}} = \frac{{y - 1}}{{\frac{{39}}{{11}} - 1}} \Leftrightarrow \frac{{28}}{{11}}\left( {x - 1} \right) =  - \frac{{25}}{{11}}\left( {y - 1} \right) \Leftrightarrow 28x + 25y - 53 = 0.\)

Chọn A.

Phương pháp giải:

B1: Ta có: \(C \in \Delta :\,\,x - 2y + 3 = 0 \Rightarrow C\left( {2c - 3;\,\,c} \right).\)

B2: Sử dụng công thức \(S = \frac{1}{2}.AB.d\left( {C,AB} \right).\)  Giải phương trình tìm \(c.\)

Lời giải chi tiết:

Ta có: \(C \in \Delta :\,\,x - 2y + 3 = 0 \Rightarrow C\left( {2c - 3;\,\,c} \right).\)

Phương trình đường thẳng \(AB\) là: \(\frac{{x + 4}}{{ - 2 + 4}} = \frac{{y + 1}}{{1 + 1}} \Leftrightarrow x + 4 = y + 1 \Leftrightarrow x - y + 3 = 0.\)

Có: \(\overrightarrow {AB}  = \left( {2;\,\,2} \right) \Rightarrow AB = 2\sqrt 2 .\)

\(\begin{array}{l} \Rightarrow {S_{ABC}} = \frac{1}{2}d\left( {C;\,\,AB} \right).AB\\ \Leftrightarrow 40 = \frac{1}{2}.\frac{{\left| {2c - 3 - c + 3} \right|}}{{\sqrt {1 + 1} }}.2\sqrt 2 \\ \Leftrightarrow \left| c \right| = 40 \Leftrightarrow \left[ \begin{array}{l}c = 40\\c =  - 40\end{array} \right..\end{array}\)

Chọn  B.

Phương pháp giải:

Gọi VTPT của đường thẳng \(AB\) là \(\left( {a;b} \right)\) và dựa vào tính chất góc hợp bởi đường chéo và cạnh góc vuông bằng \({45^0}\) ta tính được mối liên hệ giữa \(a,b\) và chọn theo tỷ lệ.

Lời giải chi tiết:

\(A\left( {2;3} \right) \notin \Delta :3x - y + 1 = 0 \Rightarrow \Delta \) là đường chéo \(BD\)

Phương trình \(AB:a\left( {x - 2} \right) + b\left( {y - 3} \right) = 0\)

\( \Leftrightarrow ax + by - 2a - 3b = 0\)

\(ABCD\) là hình vuông \( \Rightarrow AB\) hợp với \(BD\) góc \({45^0}\)

\(\begin{array}{l} \Rightarrow \cos {45^0} = \frac{{\left| {3a - b} \right|}}{{\sqrt {9 + 1} .\sqrt {{a^2} + {b^2}} }} = \frac{{\sqrt 2 }}{2} \Rightarrow 2.\left| {3a - b} \right| = \sqrt {20} .\sqrt {{a^2} + {b^2}} \\ \Rightarrow 4{\left( {3a - b} \right)^2} = 20\left( {{a^2} + {b^2}} \right) \Leftrightarrow 16{a^2} - 24ab - 16{b^2} = 0\\ \Rightarrow \left[ \begin{array}{l}a = 2b\\a = \frac{{ - 1}}{2}b\end{array} \right. \Rightarrow \left[ \begin{array}{l}AB:2x + y - 7 = 0\\AB: - x + 2y - 4 = 0\end{array} \right.\end{array}\)

Chọn  C.

Phương pháp giải:

Đường thẳng \(d\) cắt \(Ox\) tại \(A\left( {a;\,\,0} \right),\) cắt \(Oy\) tại \(B\left( {0;\,\,b} \right) \Rightarrow {S_{OAB}} = \frac{1}{2}\left| {ab} \right|.\)  

Lời giải chi tiết:

Đường thẳng \(d\) đi qua \(M\left( {8;\,\,6} \right)\) và có hệ số góc \(k\) có phương trình là: \(y = \,\,k\left( {x - 8} \right) + 6 \Leftrightarrow y = kx - 8k + 6.\)

Đk: \(\left\{ \begin{array}{l}k \ne 0\\ - 8k + 6 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k \ne 0\\k \ne \frac{3}{4}\end{array} \right..\)

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}d \cap Ox = \left\{ A \right\} \Rightarrow A\left( {\frac{{8k - 6}}{k};\,\,0} \right)\\d \cap Oy = \left\{ B \right\} \Rightarrow B\left( {0;\,\, - 8k + 6} \right)\end{array} \right..\\ \Rightarrow {S_{\Delta AOB}} = \frac{1}{2}OA.OB = \frac{1}{2}\left| {\frac{{8k - 6}}{k}.\left( {6 - 8k} \right)} \right| = \frac{1}{2}.\left| {\frac{{{{\left( {8k - 6} \right)}^2}}}{k}} \right| = 12\\ \Leftrightarrow {\left( {8k - 6} \right)^2} = 24\left| k \right|\\ \Leftrightarrow \left[ \begin{array}{l}64{k^2} - 96k + 36 = 24k\,\,\,\left( {k > 0} \right)\\64{k^2} - 96k + 36 =  - 24k\,\,\,\left( {k < 0} \right)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}64{k^2} - 120k + 36 = 0\\64{k^2} - 72k + 36 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}k = \frac{3}{2}\,\,\,\left( {tm} \right)\\k = \frac{3}{8}\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)

+) Với \(k = \frac{3}{2} \Rightarrow d:\,\,y = \frac{3}{2}x - 6 \Leftrightarrow 3x - 2y - 12 = 0\)

+) Với \(k = \frac{3}{8} \Rightarrow d:\,\,y = \frac{3}{8}x + 3 \Leftrightarrow 3x - 8y + 24 = 0.\)

Chọn  A.

Phương pháp giải:

Đường thẳng \(d\) cắt \(Ox\) tại \(A\left( {a;\,\,0} \right),\) cắt \(Oy\) tại \(B\left( {0;\,\,b} \right) \Rightarrow {S_{OAB}} = \frac{1}{2}\left| {ab} \right|.\)

Lời giải chi tiết:

Đường thẳng \(d\) đi qua \(Q\left( {2;\,\,3} \right)\) và có hệ số góc \(k\) có phương trình là: \(y = \,\,k\left( {x - 2} \right) + 3 \Leftrightarrow y = kx - 2k + 3.\)

Điều kiện: \(\left\{ \begin{array}{l}k \ne 0\\ - 2k + 3 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k \ne 0\\k \ne \frac{3}{2}\end{array} \right.\)

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}d \cap Ox = \left\{ A \right\} \Rightarrow A\left( {\frac{{2k - 3}}{k};\,\,0} \right)\\d \cap Oy = \left\{ B \right\} \Rightarrow B\left( {0;\,\, - 2k + 3} \right)\end{array} \right..\\ \Rightarrow {S_{\Delta AOB}} = \frac{1}{2}OA.OB = \frac{1}{2}\left| {\frac{{2k - 3}}{k}.\left( {3 - 2k} \right)} \right| = \frac{1}{2}.\left| {\frac{{{{\left( {2k - 3} \right)}^2}}}{k}} \right|\\ = \frac{1}{2}\left| {\frac{{4{k^2} - 12k + 9}}{k}} \right| = \frac{1}{2}\left| {4k + \frac{9}{k} - 12} \right|\\ \ge \frac{1}{2}\left| {2\sqrt {4k.\frac{9}{k}}  - 12} \right| = \frac{1}{2}\left| { -0} \right| = 0.\end{array}\)

Dấu  xảy ra \( \Leftrightarrow 4k = \frac{9}{k} \Leftrightarrow {k^2} = \frac{9}{4} \Leftrightarrow \left[ \begin{array}{l}k = \frac{3}{2}\,\,\,\left( {ktm} \right)\\k =  - \frac{3}{2}\end{array} \right.\)

+) Với \(k =  - \frac{3}{2}\) ta có: \(d:\,\,y =  - \frac{3}{2}x + 6 \Leftrightarrow 3x + 2y - 12 = 0.\)

Chọn  D.

Phương pháp giải:

+) Gọi \(AD\,\,\,\left( {D \in BC} \right)\) là đường phân giác từ đỉnh \(A\) của \(\Delta ABC.\)

+) Áp dụng định lý đường phân giác của \(\Delta ABC\) ta có: \(\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}} \Leftrightarrow \frac{{\overrightarrow {DB} }}{{AB}} = \frac{{\overrightarrow {CD} }}{{AC}}\)  để tìm tọa độ điểm \(D.\)

+) Lập phương trình đường thẳng đi qua hai điểm \(A\) và \(D.\)

Lời giải chi tiết:

Ta có: \(\overrightarrow {AB}  = \left( {3;\,6} \right) \Rightarrow AB = 3\sqrt 5 ;\,\,\,\overrightarrow {AC}  = \left( {4;\,\,2} \right) \Rightarrow AC = 2\sqrt 5 .\)

Gọi \(AD\,\,\,\left( {D \in BC} \right)\) là đường phân giác từ đỉnh \(A\) của \(\Delta ABC.\)

Gọi \(D\left( {a;\,\,b} \right).\)

Áp dụng định lý đường phân giác của \(\Delta ABC\) ta có: \(\dfrac{{DB}}{{AB}} = \dfrac{{DC}}{{AC}} \Leftrightarrow \dfrac{{\overrightarrow {DB} }}{{AB}} = \dfrac{{\overrightarrow {CD} }}{{AC}}\) 

\(\begin{array}{l} \Leftrightarrow \dfrac{{\left( {5 - a;\,\,5 - b} \right)}}{{3\sqrt 5 }} = \dfrac{{\left( {a - 6;\,\,b - 1} \right)}}{{2\sqrt 5 }}\\ \Leftrightarrow 2\sqrt 5 \left( {5 - a;\,\,5 - b} \right) = 3\sqrt 5 \left( { a-6;\,\, b-1} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}2\left( {5 - a} \right) = 3\left( {a - 6} \right)\\2\left( {5 - b} \right) = 3\left( {b - 1} \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}10 - 2a = 3a - 18\\10 - 2b = 3b - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{{28}}{5}\\b =  \dfrac{{13}}{5}\end{array} \right.  \Rightarrow D\left( {\dfrac{{28}}{5};\dfrac{{13}}{5}} \right) \\  \Rightarrow \overrightarrow {AD}  = \left( {\dfrac{{18}}{5};\dfrac{{18}}{5}} \right) = \dfrac{{18}}{5}\left( {1;1} \right).\end{array}\)

\( \Rightarrow \) Đường thẳng \(AD\) nhận vecto \(\left( {1;\,\,-1} \right)\) làm VTPT.

\( \Rightarrow AD:\,\,x - 2 - y - 1 = 0 \Leftrightarrow x - y - 3 = 0.\)

Chọn  D.