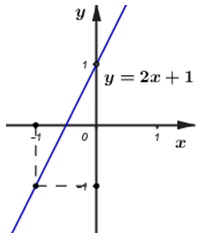
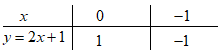50 bài tập vận dụng Ôn tập chương 2: Hàm số bậc nhấtLàm bàiQuảng cáo
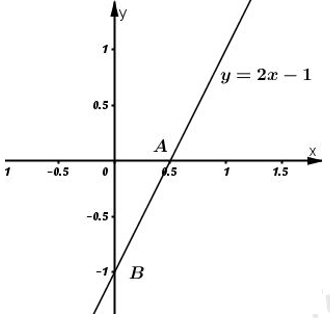
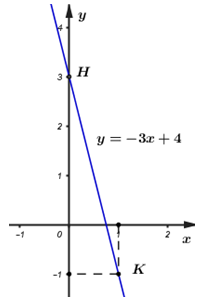
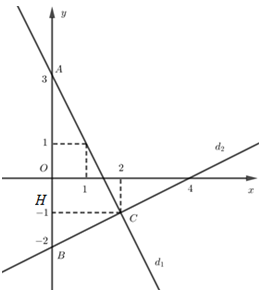
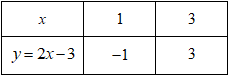
Câu hỏi 1 : Cho đường thẳng \(\left( d \right):\,\,y=\left( {{m}^{2}}+1 \right)x+m-2\), với m là tham số. a) Khi \(m=1,\) tính diện tích tam giác tạo bởi đường thẳng (d) và hai trục tọa độ. b) Tìm các giá trị của m để đường thẳng (d) song song với đường thẳng \(y=2x-3.\) c) Tìm các giá trị của m để đường thẳng (d) cắt các trục Ox, Oy lần lượt tại A và B sao cho tam giác AOB vuông cân. Phương pháp giải: Phương pháp: Câu a: Thay \(m=1\) vào phương trình đường thẳng (d), tìm giao điểm A, B của đường thẳng (d) với các trục tọa độ. Khi đó tam giác OAB là tam giác vuông tại O có diện tích: \({{S}_{OAB}}=\frac{1}{2}OA.OB.\) Câu b: Cho hai đồ thị hàm số: \({{d}_{1}}:\,\,\,y={{a}_{1}}x+{{b}_{1}};\,\,\,{{d}_{2}}:\,\,\,y={{a}_{2}}x+{{b}_{2}}\). Ta có:\({{d}_{1}}//{{d}_{2}}\Leftrightarrow \left\{ \begin{align} & {{a}_{1}}={{a}_{2}} \\ & {{b}_{1}}\ne {{b}_{2}} \\ \end{align} \right..\) Câu c: Xác định tọa độ giao điểm A và B của (d) với trục Ox, Oy theo m. Khi đó ta có tam giác OAB vuông tại O. Để tam giác OAB vuông cân thì \(OA=OB.\) Lời giải chi tiết: Giải: a) Với \(m=1\) ta có \(\left( d \right):\,\,\,y=2x-1.\) Gọi A và B lần lượt là giao điểm của (d) với Ox và Oy. Khi đó ta có: \(A\left( \frac{1}{2};0 \right)\) và \(B\left( 0;-1 \right).\) Khi đó: \({{S}_{OAB}}=\frac{1}{2}OA.OB=\frac{1}{2}.\frac{1}{2}.\left| -1 \right|=\frac{1}{4}\,\,\,\left( dvdt \right).\) b) Đường thẳng (d) song song với đường thẳng \(y = 2x - 3 \Leftrightarrow \left\{ \begin{array}{l}{m^2} + 1 = 2\\m - 2 \ne - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} = 1\\m \ne - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 1\\m = - 1\end{array} \right.\\m \ne - 1\end{array} \right. \Leftrightarrow m = 1.\) Vậy với \(m=1\) thì đường thẳng (d) song song với đường thẳng \(y=2x-3.\) c) Gọi A và và B lần lượt là giao điểm của (d) với Ox và Oy. Khi đó ta có: \(A\left( -\frac{m-2}{{{m}^{2}}+1};0 \right)\) và \(B\left( 0;m-2 \right).\) Để \(\Delta OAB\) vuông cân thì \(OA=OB\Leftrightarrow \left| -\frac{m-2}{{{m}^{2}}+1} \right|=\left| m-2 \right|\) \(\begin{array}{l} \Leftrightarrow \frac{{\left| {m - 2} \right|}}{{{m^2} + 1}} = \left| {m - 2} \right| \Leftrightarrow \left| {m - 2} \right|\left( {\frac{1}{{{m^2} + 1}} - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 2 = 0\\\frac{1}{{{m^2} + 1}} - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 2\\1 - {m^2} - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 2\\m = 0\end{array} \right.\end{array}\) Vậy với \(m=0\) hoặc \(m=2\) thì \(\Delta OAB\) vuông cân Câu hỏi 2 : Cho đường thẳng \(d:y = mx + m - 1\). Tìm \(m\) để d cắt \(Ox\) tại \(A\) và cắt \(Oy\) tại \(B\) sao cho tam giác \(AOB\) vuông cân.
Đáp án: D Phương pháp giải: : Sử dụng kiến thức - Tìm tọa độ giao điểm của đường thẳng và 2 trục tọa độ. - Điều kiện để có tam giác cân. - Giải phương trình chứa dấu giá trị tuyệt đối. Lời giải chi tiết: \(\begin{array}{l}d \cap Oy = \left\{ B \right\}\\x = 0 \Rightarrow y = m - 1\\\Rightarrow B(0;m - 1) \Rightarrow OB = |m - 1|\\d \cap {\rm{Ox}} = \left\{ A \right\}\\y = 0 \Leftrightarrow mx + m - 1 = 0 \Leftrightarrow x = \frac{{1 - m}}{m}(m \ne 0)\\\Rightarrow A\left( {\frac{{1 - m}}{m};0} \right) \Rightarrow OA = \left| {\frac{{1 - m}}{m}} \right|\end{array}\) Tam giác OAB vuông cân tại O \(\begin{array}{l} \Leftrightarrow OA = OB \Leftrightarrow |m - 1| = \left| {\frac{{1 - m}}{m}} \right|\\ \Leftrightarrow \left[ \begin{array}{l}m - 1 = \frac{{1 - m}}{m}\\m - 1 = \frac{{m - 1}}{m}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{m^2} = 1\\(m - 1)\left( {1 - \frac{1}{m}} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = \pm 1\\\frac{{{{\left( {m - 1} \right)}^2}}}{m} = 0\end{array} \right. \Leftrightarrow m = \pm 1\end{array}\) Chọn D. Câu hỏi 3 : a) Để giúp gia đình trang trải chi phí học tập , bạn An xin làm thêm tại một quán nọ và bạn ấy được trả 40 000 đồng cho mỗi giờ làm việc tại quán. Hỏi sau 1 tuần làm việc bạn An nhận được bao nhiêu tiền? Biết rằng bạn làm hết tuần không nghỉ ngày nào và do phải đi học nên mỗi ngày bạn chỉ làm 4 tiếng. b) Nếu mỗi giờ làm thêm tăng ca bạn An được trả thêm 50% số tiền mà mỗi giờ bạn ấy kiếm được trong giờ làm việc bình thường thì trong tuần đó mỗi ngày bạn phải làm thêm bao nhiêu giờ để sau một tuần bạn được trả 1 960 000 đồng? (An làm tăng ca tất cả các ngày trong tuần, số giờ tăng ca mỗi ngày là như nhau)
Đáp án: C Phương pháp giải: Lời giải chi tiết: a) Thời gian mà bạn An làm việc ở quán trong một tuần: \(4.7 = 28\) (giờ) Số tiền mà bạn An nhận được sau một tuần làm việc ở quán:\({28.40^{}}000 = {1^{}}{120^{}}000\) (đồng) b) Do bạn An được trả thêm 50% số tiền mà mỗi giờ bạn ấy kiếm được trong giờ làm việc bình thường nên mỗi giờ làm thêm bạn được trả số tiền là: \({40^{}}000 + {40^{}}000.50\% = {60^{}}000\) (đồng) Trong một tuần, số tiền có được do làm thêm của bạn An là:\({1^{}}{960^{}}000 - {1^{}}{120^{}}000 = {840^{}}000\) (đồng) Một tuần, bạn An làm thêm số giờ là:\({840^{}}000:{60^{}}000 = 14\) (giờ) Mỗi ngày bạn An phải làm thêm số giờ là:\(14:7 = 2\) (giờ) Câu hỏi 4 : Một bóng đèn sợi đốt giá 5000 đồng có công suất 60W và thời gian thắp sáng tối đa là 1000h. Một bóng đèn compact giá 50.000 đồng có công suất 15W và thời gian thắp sáng tối đa là 8000h. Hai đèn có độ sáng tương đương nhau. Giá tiền 1KW.h điện là 1800 đồng. Tính chi phí cho việc sử dụng mỗi loại đèn trên trong 8000h.
Đáp án: C Phương pháp giải: Lời giải chi tiết:
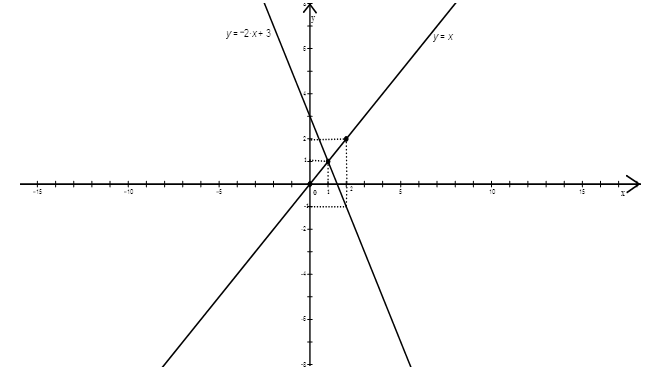
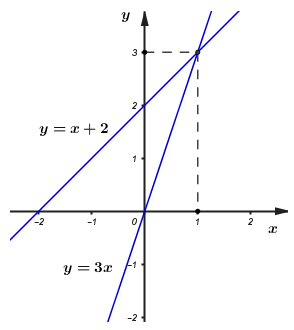
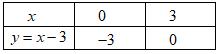
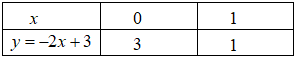
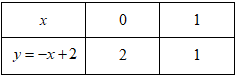
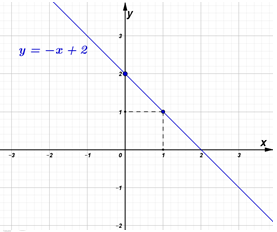
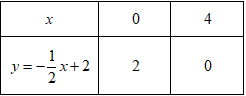
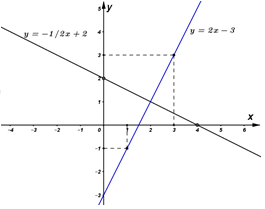
· Vì mỗi bóng đèn sợi đốt thắp sáng được tối đa 1000h nên để thắp sáng được 8000h thì cần: (bóng đèn)Điện năng tiêu thụ của mỗi bóng đèn sợi đốt (thắp sáng trong t =1000h) là: \({A_1} = P.t = 0,06.1000 = 60KWh\) \(\left( {P = 60W = 0,06KW} \right)\) Để thắp sáng trong 8000h cần sử dụng 8 bóng đèn, nên điện năng tiêu thụ của bóng đèn sợi đốt trong 8000h là:\(A = 8.{A_1} = 8.60 = 480KWh\) Tiền điện phải trả khi thắp sáng bằng đèn sợi đốt trong 8000h là:\(T = 480.1800 = 864.000\) (đồng) Tổng chi phí (bao gồm tiền mua bóng đèn và tiền điện) khi thắp sáng bằng đèn sợi đốt trong 8000h là:\({T_{tc}} = 8.5000 + 864000 = 904000\) (đồng) Do thời gian thắp sáng tối đa của đèn compact là 8000h nên ta chỉ cần dùng 1 bóng đèn compact. Điện năng tiêu thụ của một bóng đèn compact (thắp sáng trong t’= 8000h) là:\({A_{compact}} = P'.t' = 0,015.8000 = 120KWh\) \(\left( {P' = 15W = 0,015KW} \right)\) Tiền điện phải trả khi thắp sáng bằng đèn compact trong 8000h là:\({T_{compact}} = 120.1800 = 216000\) (đồng) Tổng chi phí (bao gồm tiền mua bóng đèn và tiền điện) khi thắp sáng bằng đèn compact trong 8000h là:\(T{'_{compact}} = 50000 + 216000 = 266000\) (đồng) Do: \({T_{tc}} > T{'_{compact}}\) (904000 đồng > 266000 đồng), nên ta sử dụng đèn compact sẽ có lợi hơn (cụ thể tiết kiệm được: 904000 -266000 = 638000 đồng) · Vì mỗi bóng đèn sợi đốt thắp sáng được tối đa 1000h nên để thắp sáng được 8000h thì cần:(bóng đèn) Câu hỏi 5 : a) Một khu vườn hình chữ nhật có kích thước là 25m và 40m. Người ta tăng mỗi kích thước của khu vườn thêm x (mét). Gọi S và P theo thứ tự là diện tích và chu vi của khu vườn mới tính theo x. Hỏi các đại lượng S và P có phải là hàm số bậc nhất của x không? Vì sao? Tính giá trị của x khi biết giá trị tương ứng của P là 144 (tính theo đơn vị mét). b) Cho hàm số y = -2x + 3 có đồ thị là (d1) và hàm số y = x có đồ thị là (d2). Vẽ (d1) và (d2) trên cùng mặt phẳng tọa độ Oxy. Tìm tọa độ giao điểm của (d1) và (d2) bằng phép tính.
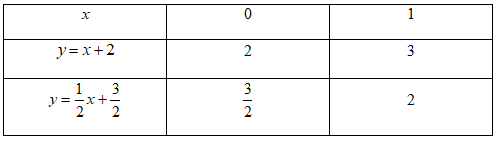
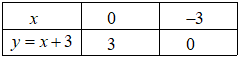
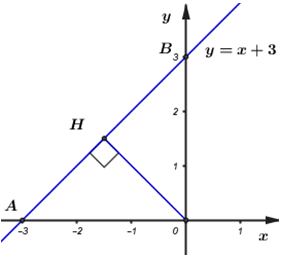
Đáp án: B Phương pháp giải: Lời giải chi tiết: a) Chiều rộng của khu vườn sau khi tăng thêm x(m) là: \(25 + x\) (mét) Chiều dài của khu vườn sau khi tăng thêm x(m) là: \(40 + x\) (mét) Chu vi của khu vườn mới là: \(P = \left( {25 + x + 40 + x} \right).2 = \left( {65 + 2x} \right).2 = 4x + {130^{}}\left( m \right)\) Diện tích của khu vườn mới là: \(S = \left( {25 + x} \right).\left( {40 + x} \right) = {x^2} + 65x + {1000^{}}\left( {{m^2}} \right)\) Do: \(P = 4x + 130\) có dạng \(y = ax + b\) với \(a = 4 \ne 0\), \(b = 130\) nên \(P = 4x + 130\) là hàm số bậc nhất. Do: \(S = {x^2} + 65x + 1000\) không có dạng \(y = ax + b\) nên không phải là hàm số bậc nhất. v Với P = 144 (m), thay vào \(P = 4x + 130\), ta được: \(144 = 4x + 130 \Leftrightarrow 4x = 14 \Leftrightarrow x = 3,5\left( m \right)\) b) Bảng giá trị:
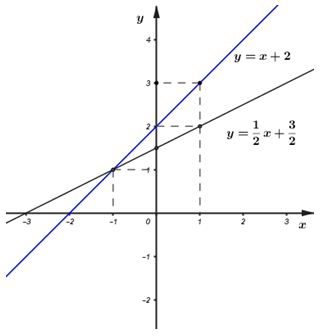
Đồ thị:
Phương trình hoành độ giao điểm của (d1) và (d2): \( - 2x + 3 = x \Leftrightarrow 3x = 3 \Leftrightarrow x = 1\) Thay x = 1 vào (d2) \( \Rightarrow y = 1\) Vậy: Tọa độ giao điểm của (d1) và (d2) là \(\left( {1{;^{}}1} \right)\).
Câu hỏi 6 : Để đổi nhiệt độ từ F (Fahrenheit) sang độ C (Celsius) ta dùng công thức: \(C = \dfrac{5}{9}\left( {F - 32} \right)\) a) C có phải là hàm số bậc nhất theo biến số F không? Giải thích. b) Hãy tính C khi F = 30; F = 80 c) Hãy tính F khi C = -10
Đáp án: D Phương pháp giải: Lời giải chi tiết: a) Ta có: \(C = \dfrac{5}{9}\left( {F - 32} \right) \Leftrightarrow C = \dfrac{5}{9}F - \dfrac{{160}}{9}\) (*) Hàm số \(C = \dfrac{5}{9}F - \dfrac{{160}}{9}\) (theo biến số F) có dạng \(y = ax + b\) với \(a = \dfrac{5}{9} \ne 0\), \(b = - \dfrac{{160}}{9}\) nên \(C = \dfrac{5}{9}F - \dfrac{{160}}{9}\) là hàm số bậc nhất theo biến số F. b) Khi F = 30, thế vào (*) \( \Rightarrow C = \dfrac{5}{9}.30 - \dfrac{{160}}{9} = - \dfrac{{10}}{9}\) (0C) Khi F = 80, thế vào (*) \( \Rightarrow C = \dfrac{5}{9}.80 - \dfrac{{160}}{9} = \dfrac{{80}}{3}\)(0C) c) Khi C = -10 (0C), thế vào (*) \( \Rightarrow - 10 = \dfrac{5}{9}.F - \dfrac{{160}}{9} \Leftrightarrow \dfrac{5}{9}.F = - 10 + \dfrac{{160}}{9} \Leftrightarrow \dfrac{5}{9}.F = \dfrac{{70}}{9} \Leftrightarrow F = \dfrac{{70}}{9}:\dfrac{5}{9} \Leftrightarrow F = 14\) Câu hỏi 7 : a) Trong một tòa nhà ngoài thang máy, người ta còn xây thêm một cầu thang đi bộ. Từ tầng 1 đến tầng 2 có 30 bậc thang. Các tầng còn lại cứ hai tầng liên tiếp cách nhau 21 bậc thang. Do thang máy bị hư nên bạn Vy đi bộ bắt đầu từ tầng 1 về căn hộ của mình. Tổng số bậc thang Vy đã đi là 135. Hỏi căn hộ của Vy ở tầng thứ bao nhiêu của tòa nhà? b) Một công nhân làm việc với mức lương cơ bản là 200 000 đồng cho 8 giờ làm việc trong một ngày. Nếu trong một tháng người đó làm 26 ngày và tăng ca thêm 3 giờ / ngày trong 10 ngày thì người đó nhận được bao nhiêu tiền lương? Biết rằng tiền lương tăng ca bằng 150% tiền lương cơ bản.
Đáp án: A Phương pháp giải: Lời giải chi tiết: a) Cách 1: Gọi x là số tầng mà bạn Vy đi qua tính từ tầng 2 đến căn hộ của mình (\(x \in N*\)) Theo đề bài ta có phương trình: \(30 + 21.x = 135 \Leftrightarrow 21x = 105 \Leftrightarrow x = {5^{}}\left( n \right)\) Vậy để đi từ tầng 1 đến căn hộ của mình thì bạn Vy phải đi qua tất cả 6 tầng, do đó căn hộ của bạn Vy ở tầng thứ 7 của tòa nhà.
Cách 2: Số bậc thang tính từ tầng 2 đến căn hộ của bạn Vy là: \(135 - 30 = 105\) (bậc thang) Số tầng mà bạn Vy phải đi qua tính từ tầng 2 đến căn hộ của bạn là: \(105:21 = 5\) (tầng) Vậy để đi từ tầng 1 đến căn hộ của mình thì bạn Vy phải đi qua tất cả 6 tầng, do đó căn hộ của bạn Vy ở tầng thứ 7 của tòa nhà. b) Tiền lương cơ bản mà người công nhân nhận được sau 26 ngày làm việc là: \({200^{}}{000.^{}}26 = {5^{}}{200^{}}000\) (đồng) Tiền lương cơ bản người công nhận được trong 1 giờ làm việc là: \({200^{}}000:8 = {25^{}}000\) (đồng) Tiền lương tăng ca trong 1 giờ của người công nhân là: \({25^{}}{000^{}}.150\% = {37^{}}500\) (đồng) Trong một ngày (tăng ca 3 giờ), số tiền do làm tăng ca mà người công nhân nhận được là: \({37^{}}{500.^{}}3 = {112^{}}500\) (đồng) Trong 10 ngày, số tiền do làm tăng ca mà người công nhân nhận được là: \({112^{}}{500.^{}}10 = {1^{}}{125^{}}000\) (đồng) Vậy tổng số tiền mà người công nhân nhận được sau 1 tháng làm việc (bao gồm cả lương cơ bản và lương do tăng ca) là: \({5^{}}{200^{}}000 + {1^{}}{125^{}}000 = {6^{}}{325^{}}000\) (đồng) Câu hỏi 8 : Giám đốc dự án xây dựng một chung cư đang phân vân giữa hai phương án: mua hoặc thuê 4 xe tải. Nếu mua thì giá một chiếc xe là 250 triệu đồng và mỗi ngày tốn chi phí là 2 triệu đồng. Còn nếu thuê thì giá một chiếc xe tốn 1 triệu đồng mỗi ngày. Viết hàm số biễu diễn chi phí cho từng phương án trong thời gian x ngày?
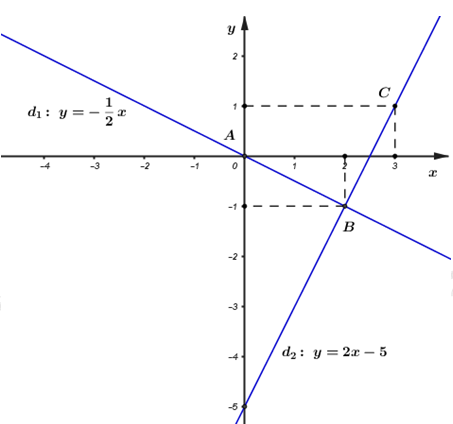
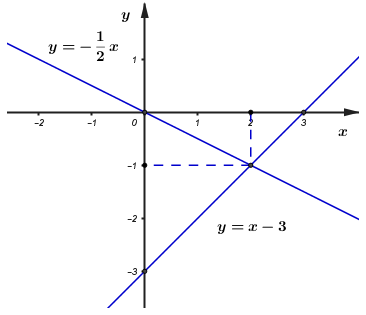
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đối với phương ấn thứ nhất (mua 4 chiếc xe) Số tiền dùng để mua 4 chiếc xe là: \(250.4=1000\) (triệu đồng), (tức là 1 tỳ đồng) Mỗi ngày tốn chi phí là 2 triệu đồng \(\Rightarrow \) x ngày tốn chi phí là 2x (triệu đồng) Hàm số biễu diễn chi phí cho phương án thứ nhất: \(y=1000+2x\)Đối với phương án thứ hai (thuê 4 chiếc xe) Giá mỗi chiếc xe thuê trong một ngày là 1 triệu đồng \(\Rightarrow \) thuê 4 chiếc xe trong một ngày mất số tiền là: \(4.1=4\) (triệu đồng) Nếu thuê 4 chiếc xe trong x ngày thì mất số tiền là: \(4.x\) (triệu đồng) Hàm số biễu diễn chi phí cho phương án thứ nhất: \(y=4x\)Câu hỏi 9 : Cho hai hàm số bậc nhất \(y=-\frac{1}{2}x\) có đồ thị là \(\left( {{d}_{1}} \right)\) và \(y=2x-5\) có đồ thị là \(\left( {{d}_{2}} \right)\) a) Vẽ \(\left( {{d}_{1}} \right),\left( {{d}_{2}} \right)\) trên cùng hệ trục tọa độ. b) Cho đường thẳng \(\left( {{d}_{3}} \right):y=ax+b.\) Tìm \(a,b\) để \({{d}_{3}}//{{d}_{1}}\) và cắt \(\left( {{d}_{2}} \right)\) tại một điểm có tung độ bằng 3.
Đáp án: C Phương pháp giải: a) Đối với đồ thị hàm số bậc nhất, đồ thị hàm số luôn là một đường thẳng. Ta chỉ cần xác định được hai điểm nằm trên đồ thị, đường thẳng đi qua hai điểm đó chính là đồ thị hàm số cần vẽ. b) Cho\(\left\{ \begin{array}{l} Lời giải chi tiết: a) Vẽ \(\left( {{d}_{1}} \right),\left( {{d}_{2}} \right)\) trên cùng hệ trục tọa độ. Ta thấy : +) \(A\left( 0;0 \right),B\left( 2;-1 \right)\) thuộc đồ thị hàm số \(y=-\frac{1}{2}x\) . +) \(B\left( 2;-1 \right),C\left( 3;1 \right)\) thuộc đồ thị hàm số \(y=2x-5\) Từ đó ta có đồ thị của hai hàm số: b) Cho đường thẳng \(\left( {{d}_{3}} \right):y=ax+b.\) Tìm \(a,b\) để \({{d}_{3}}//{{d}_{1}}\) và cắt \(\left( {{d}_{2}} \right)\) tại một điểm có tung độ bằng 3. Vì \({{d}_{3}}//{{d}_{1}}\) nên ta có: \(a=\frac{-1}{2},\ \ b\ne 0\Rightarrow {{d}_{3}}:\ \ y=-\frac{1}{2}x+b\) Theo đề bài \(\left( {{d}_{3}} \right)\) cắt \(\left( {{d}_{2}} \right)\) tại một điểm có tung độ bằng \(3\Rightarrow 3=2x-5\Rightarrow x=4\) Suy ra \(\left( {{d}_{3}} \right)\) đi qua điểm \(M\left( 4;3 \right)\)\(\Rightarrow 4.\frac{-1}{2}+b=3\Rightarrow b=5\ \ \left( tm \right)\) Vậy phương trình đường thẳng \(\left( {{d}_{3}} \right)\) là: \(y=-\frac{1}{2}x+5\) Chọn C Câu hỏi 10 : Cho hàm số bậc nhất \(y=\left( 2m-1 \right)x+3\) có đồ thị là đường thẳng \(\left( d \right).\) a) Vẽ đồ thị hàm số \(m=\frac{3}{2}.\) b) Tìm \(m\) để đường thẳng \(\left( d \right)\) và hai đường thẳng \(y=x+3\) và \(y=2x+1\) đồng quy? c) Gọi hai điểm \(A\) và \(B\) là giao điểm của \(\left( d \right)\) với lần lượt hai trục \(Ox,\ Oy.\) Tìm \(m\) để diện tích tam giác \(OAB\) bằng \(3\) (đvdt)?
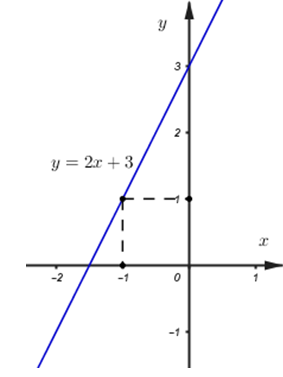
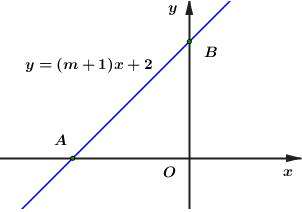
Đáp án: B Phương pháp giải: a) Thay giá trị \(m=\frac{3}{2}\) vào công thức và vẽ đồ thị hàm số trên hệ trục tọa độ. b) Tìm giao điểm M của hai đường thẳng đã cho. Để ba đường thẳng đồng quy thì (d) phải đi qua M. Thay tọa độ điểm M vào phương trình đường thẳng (d) để tìm m. c) Tìm tọa độ giao điểm A, B của (d) và các trục tọa độ sau đó dựa vào công thức tính diện tích tam giác vuông để tìm m. Ta có: \({{S}_{OAB}}=\frac{1}{2}OA.OB.\) Lời giải chi tiết: a) Vẽ đồ thị hàm số \(m=\frac{3}{2}.\) Với \(m=\frac{3}{2}\) ta có: \(\left( d \right):\ y=2x+3.\) Ta có bảng giá trị:
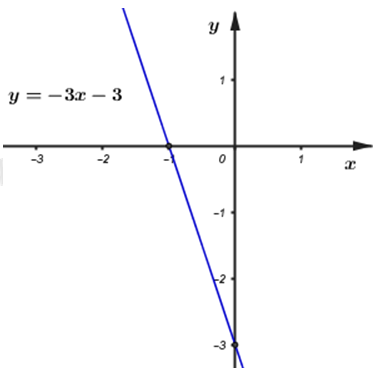
b) Tìm \(m\) để đường thẳng \(\left( d \right)\) và hai đường thẳng \(y=x+3\) và \(y=2x+1\) đồng quy? Tọa độ giao điểm của hai đường thẳng \(y=x+3\) và \(y=2x+1\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l} Đường thẳng \(\left( d \right)\) và hai đường thẳng \(y=x+3,\ \ y=2x+1\) đồng quy \(\Leftrightarrow A\left( 2;\ 5 \right)\in \left( d \right).\) \(\Rightarrow 5=\left( 2m-1 \right).2+3\Leftrightarrow 2\left( 2m-1 \right)=2\Leftrightarrow 2m-1=1\Leftrightarrow m=1.\) Vậy \(m=1\) thỏa mãn bài toán. c) Gọi hai điểm \(A\) và \(B\) là giao điểm của \(\left( d \right)\) với lần lượt hai trục \(Ox,\ Oy.\) Tìm \(m\) để diện tích tam giác \(OAB\) bằng \(3\) (đvdt)? Hàm số đã cho là hàm số bậc nhất nên \(2m-1\ne 0\Leftrightarrow m\ne \frac{1}{2}.\) Gọi hai điểm \(A\) và \(B\) là giao điểm của \(\left( d \right)\) với lần lượt hai trục \(Ox,\ Oy.\) \(\Rightarrow A\left( -\frac{3}{2m-1};\ 0 \right),\ \ B\left( 0;\ 3 \right)\) Khi đó ta có \(\Delta OAB\) vuông tại \(O.\) \(\begin{array}{l} Vậy \(m=\frac{5}{4},\ \ m=-\frac{1}{4}\) thỏa mãn điều kiện bài toán. Chọn B Câu hỏi 11 : Cho đường thẳng \(\left( {{d_1}} \right) :y = \left( {m - 1} \right)x + 2m + 1\) a) Tìm \(m\) để đường thẳng \({{d}_{1}}\) cắt trục tung tại điểm có tung độ là \(-3\) Vẽ đồ thị hàm số vừa tìm được và chứng tỏ giao điểm của đồ thị hàm số vừa tìm được với đường thẳng \(\left( d \right):y=x+1\) nằm trên trục hoành. b) Tìm \(m\) để khoảng cách từ gốc tọa độ đến đường thẳng \({{d}_{1}}\) đạt giá trị lớn nhất.
Đáp án: D Phương pháp giải: a) Vì đã có tọa độ giao điểm của đường thẳng với trục tung, thay tọa độ đó vào phương trình đường thẳng để tìm \(m\) Tìm tọa độ giao điểm của đường thẳng vừa tìm được với \(\left( d \right):y=x+1\) bằng cách lập phương trình hoành độ giao điểm, sau đó chứng minh giao điểm đó cũng nằm trên trục hoành. b) Gọi A, B là giao điểm của đường thẳng với trục tung và trục hoành. Độ dài đường cao ứng với đỉnh O trong tam giác vuông OAB chính là khoảng cách từ gốc tọa độ tới đường thẳng. Áp dụng hệ thức lượng trong tam giác vuông để tính từ đó biện luận tìm giá trị lớn nhất. Từ đó tìm giá trị của m. Lời giải chi tiết: a) Tìm \(m\) để đường thẳng \({{d}_{1}}\) cắt trục tung tại điểm có tung độ là \(-3\) Vẽ đồ thị hàm số vừa tìm được và chứng tỏ giao điểm của đồ thị hàm số vừa tìm được với đường thẳng \(\left( d \right):y=x+1\) nằm trên trục hoành. Vì \({{d}_{1}}\) cắt trục tung tại điểm có tung độ là \(-3\) suy ra \(\left( 0;-3 \right)\) nằm trên đường thẳng \({{d}_{1}}\) \(\Rightarrow -3=\left( m-1 \right).0+2m+1\Leftrightarrow 2m=-4\Leftrightarrow m=-2\) Với \(m=-2\) ta có phương trình đường thẳng \(\left( {{d}_{1}} \right):y=-3x-3\) Nhận thấy: \(A\left( 0;-3 \right),\ B\left( -1;\ 0 \right)\) nằm trên đồ thị hàm số. Vì hàm số \(\left( {{d}_{1}} \right):y=-3x-3\) là hàm số bậc nhất nên đồ thị của nó có dạng đường thẳng, từ đó ta có đồ thị: Hoành độ giao điểm của \(\left( {{d}_{1}} \right):y=-3x-3\) và \(\left( d \right):y=x+1\) là nghiệm của phương trình: \(x+1=-3x-3\Leftrightarrow 4x=-4\Leftrightarrow x=-1\Rightarrow y=x+1=-1+1=0\) Vậy giao điểm của \(\left( {{d}_{1}} \right):y=-3x-3\) và \(\left( d \right):y=x+1\) là \(\left( -1;0 \right)\) Nhận thấy điểm \(\left( -1;0 \right)\) nằm trên trục hoành (do có tung độ bằng 0). Vậy ta có điều cần chứng minh b) Tìm \(m\) để khoảng cách từ gốc tọa độ đến đường thẳng \({{d}_{1}}\) đạt giá trị lớn nhất. +) Với \(x=0\Rightarrow y=2m+1\Rightarrow A\left( 0;2m+1 \right)\) là giao điểm của \({{d}_{1}}\) với trục tung\(\Rightarrow OA=\left| 2m+1 \right|\) +) Với \(y=0\Rightarrow x=\frac{-\left( 2m+1 \right)}{m-1}\Rightarrow B\left( \frac{-\left( 2m+1 \right)}{m-1};0 \right)\) là giao điểm của \({{d}_{1}}\) với trục hoành \(\Rightarrow OB=\left| \frac{-\left( 2m+1 \right)}{m-1} \right|\) Từ O kẻ đường cao OH với, ta được OH chính là khoảng cách từ O tới \({{d}_{1}}\) Xét tam giác vuông OAB vuông tại O có đường cao OH \(\Rightarrow \frac{1}{O{{H}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}\) (hệ thức lượng trong tam giác vuông) Đặt \(\frac{1}{O{{H}^{2}}}=t\) ta có: \(\begin{align} & t=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}=\frac{1}{{{\left( 2m+1 \right)}^{2}}}+\frac{{{\left( m-1 \right)}^{2}}}{{{\left( 2m+1 \right)}^{2}}}=\frac{{{m}^{2}}-2m+2}{4{{m}^{2}}+4m+1}\ \ \ \left( m\ne -\frac{1}{2} \right) \\ & \Leftrightarrow 4{{m}^{2}}t+4mt+t={{m}^{2}}-2m+2 \\ & \Rightarrow {{m}^{2}}\left( 4t-1 \right)+2m\left( 2t+1 \right)+t-2=0 \\ \end{align}\) Coi đây là phương trình bậc 2 ẩn \(m\) phương trình có nghiệm khi \(\) \(\) \(\) \(\begin{align} & \Delta '={{\left( 2t+1 \right)}^{2}}-\left( 4t-1 \right)\left( t-2 \right)\ge 0 \\ & \Leftrightarrow 4{{t}^{2}}+4t+1-4{{t}^{2}}+9t-2\ge 0 \\ & \Leftrightarrow 13t-1\ge 0\Leftrightarrow t\ge \frac{1}{13} \\ & \Rightarrow \frac{1}{O{{H}^{2}}}\ge \frac{1}{13}\Rightarrow OH\le \sqrt{13} \\ \end{align}\) Dấu “=” xảy ra khi phương trình có nghiệm kép \(\) \(\Leftrightarrow m=\frac{-b}{2a}=\frac{-\left( 4t+2 \right)}{2\left( 4t-1 \right)}=-\frac{\frac{4}{13}+2}{2.\left( \frac{4}{13}-1 \right)}=\frac{5}{3}\ \ \ \left( tm \right)\) Vậy \(m=\frac{5}{3}\) là giá trị cần tìm. Chọn D Câu hỏi 12 : Cho hàm số \(y = 3x + 2\) có đồ thị là đường thẳng \(\left( {{d_1}} \right).\) 1. Điểm \(A\left( {\frac{1}{3};3} \right)\) có thuộc đường thẳng \(\left( {{d_1}} \right)\) không? Vì sao? 2. Tìm giá trị của \(m\) để đường thẳng \(\left( {{d_1}} \right)\) và đường thẳng \(\left( {{d_2}} \right)\) có phương trình \(y = - 2x - m\) cắt nhau tại điểm có hoành độ bằng 1.
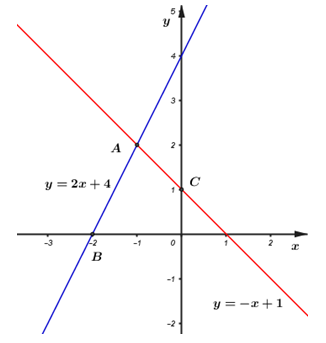
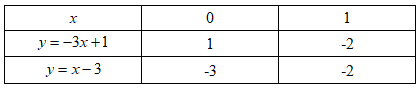
Đáp án: A Phương pháp giải: 1. Thay tọa độ điểm A vào hàm số. Nếu thỏa mãn thì điểm A thuộc đồ thị \(\left( {{d_1}} \right)\) và ngược lại. 2. Lập phương trình hoành độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\). \(\left( {{d_1}} \right)\) cắt \(\left( {{d_2}} \right)\) tại điểm có hoành độ bằng 1. Thay \(x = 1\) vào phương trình hoành độ giao điểm để tìm m. Lời giải chi tiết: Cho hàm số \(y = 3x + 2\) có đồ thị là đường thẳng \(\left( {{d_1}} \right).\) 1. Điểm \(A\left( {\frac{1}{3};3} \right)\) có thuộc đường thẳng \(\left( {{d_1}} \right)\) không? Vì sao? Thay tọa độ điểm A vào công thức hàm số ta có: \(3.\frac{1}{3} + 2 = 1 + 2 = 3\) . Vậy \(A\left( {\frac{1}{3};3} \right)\) thuộc đường thẳng \(\left( {{d_1}} \right):y = 3x + 2\) 2. Tìm giá trị của \(m\) để đường thẳng \(\left( {{d_1}} \right)\) và đường thẳng \(\left( {{d_2}} \right)\) có phương trình \(y = - 2x - m\) cắt nhau tại điểm có hoành độ bằng 1. Phương trình hoành độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là: \(3x + 2 = - 2x - m \Leftrightarrow m = - 5x - 2\) \(\left( 1 \right)\) Vì \(\left( {{d_1}} \right)\) cắt \(\left( {{d_2}} \right)\) tại điểm có hoành độ bằng 1 nên \(x = 1\) là nghiệm của phương trình \(\left( 1 \right)\) Vậy với \(m = - 7\) thỏa mãn yêu cầu để bài. Chọn A. Câu hỏi 13 : Cho hàm số \(y = 2x + 4\) có đồ thị là \(\left( {{d_1}} \right)\)và hàm số \(y = - x + 1\) có đồ thị là \(\left( {{d_2}} \right)\) 1) Vẽ \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ . 2) Gọi A là giao điểm của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\). Tìm tọa độ của điểm A. 3) Xác định các hệ số \(a,b\) của đường thẳng \({d_3}:y = ax + b\). Biết rằng \(\left( {{d_3}} \right)\)song song với \(\left( {{d_1}} \right)\) và \(\left( {{d_3}} \right)\)cắt \(\left( {{d_2}} \right)\) tại một điểm có hoành độ bằng 2.
Đáp án: C Phương pháp giải: 1) Nhận thấy hai hàm số \(y = 2x + 4\) và \(y = - x + 1\) là hai hàm bậc nhất, nên đồ thị của chúng có dạng đường thẳng. Để vẽ dạng đồ thị này, ta xác đinh hai điểm nằm trên đồ thị, sau đó kẻ đường thẳng đi qua hai điểm đó. 2) Tìm hoành độ giao điểm của hai đường thẳng bằng cách lập phương trình hoành độ giao điểm, từ đó tìm ra tung độ, suy ra tọa độ giao điểm. 3) Hai đường thẳng phân biệt song song với nhau khi có cùng hệ số góc, tìm tọa độ giao điểm của \(\left( {{d_3}} \right)\) và \(\left( {{d_2}} \right)\) sau đó thay vào phương trình để tìm \(b\). Lời giải chi tiết: \(\) Cho hàm số \(y = 2x + 4\) có đồ thị là \(\left( {{d_1}} \right)\)và hàm số \(y = - x + 1\) có đồ thị là \(\left( {{d_2}} \right)\) 1) Vẽ \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ . +) Nhận thấy hai điểm \(A\left( { - 1;2} \right),B\left( { - 2;0} \right)\) thuộc đồ thị hàm số \(y = 2x + 4\). +) Nhận thấy hai điểm \(A\left( { - 1;2} \right),C\left( {0;1} \right)\)thuộc đồ thị hàm số \(y = - x + 1\). Từ đó ta có đồ thị của hai hàm số: 2) Gọi A là giao điểm của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\). Tìm tọa độ của điểm A. Hoành độ giao điểm của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\)là nghiệm của phương trình: \(2x + 4 = - x + 1 \Leftrightarrow 3x = - 3 \Leftrightarrow x = - 1\) Với \(x = - 1 \Rightarrow y = 2x + 4 = 2.\left( { - 1} \right) + 4 = 2\) Vậy giao điểm của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) là \(A\left( { - 1;2} \right)\)\(\) 3) Xác định các hệ số \(a,b\) của đường thẳng \({d_3}:y = ax + b\). Biết rằng \(\left( {{d_3}} \right)\)song song với \(\left( {{d_1}} \right)\) và \(\left( {{d_3}} \right)\)cắt \(\left( {{d_2}} \right)\) tại một điểm có hoành độ bằng 2. Vì \(\left( {{d_3}} \right)\)song song với \(\left( {{d_1}} \right)\)nên hai đường thẳng này có hệ số góc bằng nhau\( \Rightarrow \left\{ \begin{array}{l}a = 2\\b \ne 4\end{array} \right..\) Điểm thuộc \(\left( {{d_2}} \right)\) có hoành độ bằng 2 là \(\left( {2; - 1} \right)\). Vì \(\left( {{d_3}} \right)\)cắt \(\left( {{d_2}} \right)\) tại một điểm có hoành độ bằng 2 nên điểm\(\left( {2; - 1} \right)\) thuộc đồ thị hàm số \({d_3}:y = ax + b\) \(\begin{array}{l} \Rightarrow - 1 = a.2 + b\\ \Rightarrow b = - 1 - 2a = - 1 - 2.2 = - 5\;\;\left( {tm} \right)\end{array}\) Vậy \(a = 2,b = - 5\). Chọn C. Câu hỏi 14 : Cho hàm số \(y = \left( {2 - m} \right)x + m + 1\) (với m là tham số và \(m \ne 2\)) có đồ thị là đường thẳng \(\left( d \right).\) a) Khi \(m = 0\), hãy vẽ \(\left( d \right)\) trên hệ trục tọa độ \(Oxy\). b) Tìm m để \(\left( d \right)\) cắt đường thẳng \(y = 2x - 5\) tại điểm có hoành độ bằng 2. c) Tìm m để \(\left( d \right)\) cùng với các trục tọa độ \(Ox,\,\,Oy\) tạo thành một tam giác có diện tích bằng 2.
Đáp án: C Phương pháp giải: b) Lập phương trình hoành độ giao điểm của \(\left( d \right)\) và \(y = 2x - 5\). Hai đường thẳng cắt nhau tại điểm có hoành độ bằng 2. Thay \(x = 2\) vào phương trình hoành độ giao điểm để tìm m. c) Tìm giao điểm của \(\left( d \right)\) với hai trục tọa độ Ox, Oy là A và B. OAB là tam giác vuông tại O. \({S_{\Delta OAB}} = 2.\) Từ đó tìm m. Lời giải chi tiết: a) Khi \(m = 0\), hãy vẽ \(\left( d \right)\) trên hệ trục tọa độ \(Oxy\). Khi \(m = 0\) thì \(\left( d \right):\;\;y = 2x + 1\) Đồ thị của đường thẳng \(\left( d \right)\) đi qua 2 điểm \(\left( {0;1} \right),\,\,\,\left( {1;3} \right).\) b) Tìm m để \(\left( d \right)\) cắt đường thẳng \(y = 2x - 5\) tại điểm có hoành độ bằng 2. Phương trình hoành độ giao điểm của \(\left( d \right)\) và đường thẳng \(y = 2x - 5\) là \(\left( {2 - m} \right)x + m + 1 = 2x - 5 \Leftrightarrow mx = m + 6\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\) Để \(\left( d \right)\) cắt đường thẳng \(y = 2x - 5\) tại điểm có hoành độ bằng 2 thì \(x = 2\) là nghiệm của phương trình \(\left( 1 \right)\) hay \(2m = m + 6 \Leftrightarrow m = 6.\) Vậy với \(m = 6\) thỏa mãn yêu cầu đề bài. c) Tìm m để \(\left( d \right)\) cùng với các trục tọa độ \(Ox,\,\,Oy\) tạo thành một tam giác có diện tích bằng 2. Gọi A và B là giao điểm của \(\left( d \right)\) lần lượt với hai trục tọa độ Ox, Oy. Tọa độ điểm A thỏa mãn \(\left\{ \begin{array}{l}y = \left( {2 - m} \right)x + m + 1\\y = 0\end{array} \right. \Leftrightarrow x = \frac{{m + 1}}{{m - 2}} \Rightarrow A\left( {\frac{{m + 1}}{{m - 2}};0} \right) \Rightarrow OA = \left| {\frac{{m + 1}}{{m - 2}}} \right|\) Tọa độ điểm B thỏa mãn \(\left\{ \begin{array}{l}y = \left( {2 - m} \right)x + m + 1\\x = 0\end{array} \right. \Leftrightarrow y = m + 1 \Rightarrow B\left( {0;m + 1} \right) \Rightarrow OB = \left| {m + 1} \right|\) \({S_{\Delta OAB}} = 2 \Leftrightarrow \frac{{OA.OB}}{2} = 2 \Leftrightarrow \left| {\frac{{m + 1}}{{m - 2}}} \right|.\left| {m + 1} \right| = 4 \Leftrightarrow {\left( {m + 1} \right)^2} = 4\left| {m - 2} \right|\) Trường hợp 1: \(m > 2 \Rightarrow pt \Leftrightarrow {\left( {m + 1} \right)^2} = 4\left( {m - 2} \right) \Leftrightarrow {m^2} - 2m + 9 = 0\) vô nghiệm. Trường hợp 2: \(m < 2 \Rightarrow pt \Leftrightarrow {\left( {m + 1} \right)^2} = - 4\left( {m - 2} \right) \Leftrightarrow {m^2} + 6m - 7 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 1\;\;\;\left( {tm} \right)\\m = - 7\;\;\left( {tm} \right)\end{array} \right.\) Vậy với \(m = 1\) hoặc \(m = - 7\) thỏa mãn yêu cầu đề bài. Chọn C. Câu hỏi 15 : Cho hàm số \(y = \left( {m + 1} \right)x + m\) (với \(m \ne - 1\) có đồ thị là đường thẳng \(\left( d \right)\) 1) Tìm giá trị của m để đường thẳng \(\left( d \right)\) cắt trục tung tại điểm có tung độ là 1 2) Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng \(\left( d \right)\) với giá trị m tìm được ở câu 1 3) Tìm giá trị của m để đường thẳng \(\left( d \right)\) cắt đường thẳng \(y = 3x + 2\) tại một điểm nằm trên trục hoành
Đáp án: A Phương pháp giải: 1) \(\left( d \right)\) cắt trục tung tại điểm có tung độ là 1, điểm đó là điểm \(\left( {0;1} \right)\). Thay tọa độ vào hàm số để tìm m 3) \(\left( d \right)\) cắt đường thẳng \(y = 3x + 2\) tại một điểm nằm trên trục hoành, tìm điểm đó rồi thay tọa độ vào hàm số để tìm m Lời giải chi tiết: Cho hàm số \(y = \left( {m + 1} \right)x + m\) (với \(m \ne - 1\) có đồ thị là đường thẳng \(\left( d \right)\) 1) Tìm giá trị của m để đường thẳng \(\left( d \right)\) cắt trục tung tại điểm có tung độ là 1 Để đường thẳng \(\left( d \right)\) cắt trục tung tại điểm có tung độ là 1 \( \Rightarrow \) Điểm \(A\left( {0;1} \right)\) thuộc \(\left( d \right)\) \( \Rightarrow 1 = \left( {m + 1} \right)0 + m \Leftrightarrow m = 1\). Vậy với \(m = 1\) đường thẳng \(\left( d \right)\) cắt trục tung tại điểm có tung độ là 1. 2) Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng \(\left( d \right)\) với giá trị m tìm được ở câu 1 Với \(m = 1\) thì \(\left( d \right):\,y = 2x + 1\) Ta có: Đồ thị hàm số \(\left( d \right):\,y = 2x + 1\) là đường thẳng đi qua hai điểm \(\left( {0;1} \right)\) và \(\left( {1;3} \right)\) 3) Tìm giá trị của m để đường thẳng \(\left( d \right)\) cắt đường thẳng \(y = 3x + 2\) tại một điểm nằm trên trục hoành Gọi đường thẳng \(\left( d \right)\) cắt đường thẳng \(y = 3x + 2\) tại một điểm B nằm trên trục hoành \( \Rightarrow \) B là giao điểm của đường thẳng \(y = 3x + 2\) với trục hoành \( \Rightarrow \,\,B\left( { - \frac{2}{3};0} \right)\) Vì B cũng thuộc \(\left( d \right)\) \( \Rightarrow 0 = \left( {m + 1} \right)\left( { - \frac{2}{3}} \right) + m \Leftrightarrow \frac{1}{3}m - \frac{2}{3} = 0 \Leftrightarrow m = 2\) Vậy với \(m = 2\) thỏa mãn yêu cầu đề bài. Chọn A. Câu hỏi 16 : Cho đường thẳng \(\left( d \right)\) có phương trình \(y = \left( {2k - 1} \right)x + k - 2\) (với k là tham số) a) Tìm giá trị của k biết đường thẳng \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right)\) có phương trình \(y = - 3x + 5\) b) Với giá trị của k tìm được ở câu a, vẽ đường thẳng \(\left( d \right)\) trên mặt phẳng tọa độ và tính khoảng cách từ gốc tọa độ O đến đường thẳng \(\left( d \right)\)
Đáp án: B Phương pháp giải: a) Áp dụng điều kiện để hai đường thẳng song song để tìm k. Cho hai đường thẳng \({d_1}:\;\;y = {a_1}x + {b_1}\) và \({d_2}:\;\;y = {a_2}x + {b_2}.\) Khi đó \({d_1}//{d_2} \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {d_2}\end{array} \right..\) b) Tìm giao điểm của \(\left( d \right)\) với các trục Ox, Oy, sau đó sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách. Lời giải chi tiết: Cho đường thẳng \(\left( d \right)\) có phương trình \(y = \left( {2k - 1} \right)x + k - 2\) (với k là tham số) a) Tìm giá trị của k biết đường thẳng \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right)\) có phương trình \(y = - 3x + 5\) \(\left( d \right)//\left( {d'} \right) \Leftrightarrow \left\{ \begin{array}{l}2k - 1 = - 3\\k - 2 \ne 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k = - 1\\k \ne 7\end{array} \right. \Leftrightarrow k = - 1\) Vậy với \(k = - 1\) thỏa mãn yêu cầu đề bài. b) Với giá trị của k tìm được ở câu a, vẽ đường thẳng \(\left( d \right)\) trên mặt phẳng tọa độ và tính khoảng cách từ gốc tọa độ O đến đường thẳng \(\left( d \right)\) Khi \(k = - 1\) thì \(\left( d \right):y = - 3x - 3\) Ta có bảng giá trị: Vậy đồ thị hàm số \(y = - 3x - 3\) là đường thẳng đi qua hai điểm \(\left( {0; - 3} \right),\;\;\left( { - 1;\;0} \right).\) Gọi A, B lần lượt là giao điểm của của \(\left( d \right)\) với Ox, Oy Cho \(x = 0\) ta được \(y = - 3\) \( \Rightarrow B\left( {0; - 3} \right)\) \( \Rightarrow OB = 3\) Cho \(y = 0\) ta được \(x = - 1\) \( \Rightarrow A\left( { - 1;0} \right)\) \( \Rightarrow OA = 1\) Gọi H là hình chiếu của O trên \(\left( d \right)\), ta có: \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} = \frac{1}{1} + \frac{1}{{{3^2}}} = \frac{{10}}{9} \Leftrightarrow OH = \frac{{3\sqrt {10} }}{{10}}\) (dvđd) Vậy khoảng cách từ gốc tọa độ O đến đường thẳng \(\left( d \right)\) là \(OH = \frac{{3\sqrt {10} }}{{10}}\) (dvđd)
Câu hỏi 17 : Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\left( d \right)\)\(:\,\,y = ax + 3\). 1) Xác định a biết \(\left( d \right)\) đi qua \(K\left( {1; - 1} \right)\). Vẽ đồ thị với a vừa tìm được. 2) Tìm tất cả các giá trị của a để đường thẳng \(\left( d \right)\) cắt Ox và Oy lần lượt tại hai điểm M và N sao cho diện tích tam giác OMN bằng 4.
Đáp án: A Phương pháp giải: 1) Thay tọa độ điểm K vào hàm số để tìm a. Thay a tìm được vào hàm số và vẽ. 2) Xác định các điểm M, N và khoảng cách OM, ON theo a. Sử dụng công thức tính diện tích tam giác vuông và dữ kiện còn lại của đề bài để tìm a Lời giải chi tiết: Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\left( d \right)\)\(:\,\,y = ax + 3\). 1) Xác định a biết \(\left( d \right)\) đi qua \(K\left( {1; - 1} \right)\). Vẽ đồ thị với a vừa tìm được. \(\left( d \right)\) đi qua \(K\left( {1; - 1} \right)\)\( \Rightarrow - 1 = a.1 + 3 \Leftrightarrow a = - 4\) Vậy với \(a = - 4\) thì \(\left( d \right)\) đi qua \(K\left( {1; - 1} \right)\) Với \(a = - 4\) thì \(\left( d \right)\,:\,\,y = - 4x + 3\) Đường thẳng \(\left( d \right)\) đi qua \(K\left( {1; - 1} \right)\) và \(H\left( {0;3} \right)\) 2) Tìm tất cả các giá trị của a để đường thẳng \(\left( d \right)\) cắt Ox và Oy lần lượt tại hai điểm M và N sao cho diện tích tam giác OMN bằng 4. Để đường thẳng \(\left( d \right)\) cắt Ox và Oy lần lượt tại hai điểm M và N \( \Leftrightarrow \,\,a \ne 0\) \(M\left( {{x_M};{y_M}} \right)\) là giao điểm của đường thẳng \(\left( d \right)\) và trục Ox \( \Rightarrow \left\{ \begin{array}{l}{y_M} = a{x_M} + 3\\{y_M} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_M} = - \frac{3}{a}\\{y_M} = 0\end{array} \right. \Rightarrow M\left( { - \frac{3}{a};0} \right) \Rightarrow OM = \left| { - \frac{3}{a}} \right| = \left| {\frac{3}{a}} \right|\) \(N\left( {{x_N};{y_N}} \right)\) là giao điểm của đường thẳng \(\left( d \right)\) và trục Oy \( \Rightarrow \left\{ \begin{array}{l}{y_N} = a{x_N} + 3\\{x_N} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_N} = 0\\{y_M} = 3\end{array} \right. \Rightarrow N\left( {0;3} \right) \Rightarrow ON = 3\) Diện tích tam giác OMN bằng 4 \( \Rightarrow {S_{\Delta OMN}} = \frac{1}{2}OM.ON = \frac{1}{2}.\left| {\frac{3}{a}} \right|.3 = \frac{9}{2}.\left| {\frac{1}{a}} \right| = 4 \Leftrightarrow \left| {\frac{1}{a}} \right| = \frac{8}{9} \Leftrightarrow \left| a \right| = \frac{9}{8} \Leftrightarrow \left[ \begin{array}{l}a = \frac{9}{8}\\a = - \frac{9}{8}\end{array} \right.\) Vậy với \(a = \frac{9}{8}\) hoặc \(a = - \frac{9}{8}\) thỏa mãn yêu cầu đề bài. Chọn A. Câu hỏi 18 : Cho đường thẳng \(\left( {{d_1}} \right):y = - 3x + 1\) và đường thẳng \(\left( {{d_2}} \right):y = x - 3\). a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng mặt phẳng tọa độ \(Oxy\). b) Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) bằng phép tính. c) Tìm \(m\) để đường thẳng \(\left( D \right):y = \left( {2m + 3} \right)x - 5\) song song vơi đường thẳng \(\left( {{d_1}} \right)\).
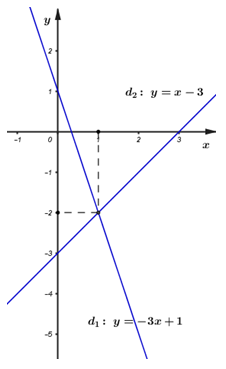
Đáp án: B Phương pháp giải: a) Nhận thấy \(\left( {{d_1}} \right):y = - 3x + 1\) và \(\left( {{d_2}} \right):y = x - 3\)là hai hàm số bậc nhất nên đồ thị của chúng có dạng đường thẳng. Để vẽ dạng đồ thị này, ta cần xác định hai điểm nằm trên đồ thị đó, sau đó kẻ đường thẳng đi qua hai điểm vừa xác định thì ta được đồ thị hàm số cần vẽ. b) Tìm hoành độ giao điểm của hai đồ thị bằng cách lập phương trình hoành độ giao điểm, từ đó tìm ra tung độ của giao điểm , cuối cùng kết luận tọa độ giao điểm tìm được. c) Hai đường thẳng song song với nhau khi chúng có cùng hệ số góc và hai đường thẳng đó không được trùng nhau. Lời giải chi tiết: a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng mặt phẳng tọa độ \(Oxy\). Ta có bảng giá trị: Vậy đường thẳng \(\left( {{d_1}} \right)\) đi qua điểm \(\left( {0;\;1} \right),\;\;\left( {1; - 2} \right)\) và đường thẳng \(\left( {{d_2}} \right)\) đi qua điểm \(\left( {0; - 3} \right),\;\;\left( {1; - 2} \right).\) Từ đó ta có đồ thị của hai hàm số: b) Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) bằng phép tính. Hoành độ giao điểm của hai đường thẳng là nghiệm của phương trình : \( - 3x + 1 = x - 3 \Leftrightarrow 4x = 4 \Leftrightarrow x = 1\). Với \(x = 1 \Rightarrow y = x - 3 = 1 - 3 = - 2\) Vậy tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\)là: \(A\left( {1; - 2} \right)\).\(\) c) Tìm \(m\) để đường thẳng \(\left( D \right):y = \left( {2m + 3} \right)x - 5\) song song với đường thẳng \(\left( {{d_1}} \right)\). Hai đường thẳng song song khi chúng có cùng hệ số góc và chúng không trùng nhau. Suy ra để đường thẳng \(\left( D \right):y = \left( {2m + 3} \right)x - 5\) song song với đường thẳng \(\left( {{d_1}} \right)\) thì: \(\left\{ \begin{array}{l}2m + 3 = - 3\\ - 5 \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2m = - 6\\ - 5 \ne 1\end{array} \right. \Leftrightarrow m = - 3\). Vậy \(m = - 3\) là giá trị cần tìm. Chọn B. Câu hỏi 19 : Cho hàm số \(y = 3x\) có đồ thị \(\left( D \right)\) và hàm số \(y = x + 2\) có đồ thị \(\left( {{D_1}} \right)\). 1) Vẽ \(\left( D \right)\) và \(\left( {{D_1}} \right)\) trên cùng một mặt phẳng tọa độ \(Oxy\). 2) Tìm \(m\) để đường thẳng \(y = \left( {m - 5} \right)x + m + 2\) có đồ thị \(\left( {{D_2}} \right)\) cắt \(\left( {{D_1}} \right)\) tại điểm B có hoành độ bằng 2.
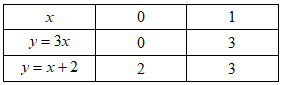
Đáp án: A Phương pháp giải: 1) Nhận thấy hai hàm số \(y = 3x\) và \(y = x + 2\) là hai hàm bậc nhất nên đồ thị của chúng có dạng đường thẳng. Để vẽ đồ thị hàm số dạng này ta cần xác định hai điểm thuộc đồ thị hàm số, sau đó vẽ đường thẳng đi qua hai điểm đó. 2) Vì điểm B có hoành độ bằng 2, từ đó tìm ra tọa độ điểm B. Thay tọa độ điểm B vào phương trình của hàm số \(y = \left( {m - 5} \right)x + m + 2\) để tìm \(m\). Lời giải chi tiết: 1) Vẽ \(\left( D \right)\)và \(\left( {{D_1}} \right)\) trên cùng một mặt phẳng tọa độ \(Oxy\). Ta có bảng giá trị: Vậy đường thẳng \(\left( D \right)\) đi qua 2 điểm \(\left( {0;\;0} \right),\;\;\left( {1;\;3} \right)\) và đường thẳng \(\left( {{D_1}} \right)\) đi qua 2 điểm \(\left( {0;\;2} \right),\;\;\left( {1;\;3} \right).\) Từ đó ta có đồ thị của hai hàm số như hình bên: 2) Tìm \(m\) để đường thẳng \(y = \left( {m - 5} \right)x + m + 2\) có đồ thị \(\left( {{D_2}} \right)\) cắt \(\left( {{D_1}} \right)\)tại điểm B có hoành độ bằng 2. Vì điểm B có hoành độ bằng 2 và thuộc \(\left( {{D_1}} \right)\)nên ta có tung độ điểm B là: \(y = x + 2 = 2 + 2 = 4\). Thay tọa độ điểm \(B\left( {2;4} \right)\) vào phương trình \(y = \left( {m - 5} \right)x + m + 2\;\;\left( {{D_2}} \right)\) có: \(2\left( {m - 5} \right) + m + 2 = 4 \Leftrightarrow 2m - 10 + m + 2 = 4 \Leftrightarrow 3m = 12 \Leftrightarrow m = 4\). Vậy \(m = 4\) là giá trị cần tìm. Chọn A. Câu hỏi 20 : Cho hàm số \(y = (m - 1)x + m\). Câu 1: Xác định giá trị của \(m\) để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng \(2\).
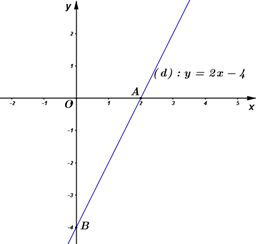
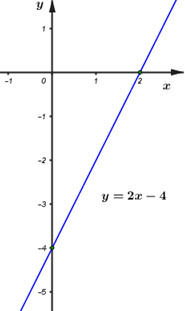
Đáp án: B Phương pháp giải: Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng \(2 \Rightarrow A\left( {0;\;2} \right)\) thuộc đồ thị hàm số. Thay tọa độ điểm A vào công thức hàm số ta tìm được giá trị của m. Lời giải chi tiết: Đồ thị của hàm số cắt trục tung tại điểm của tung độ bằng \(2\) nên đồ thị của hàm số đi qua điểm \(A(0\,;\,\,2)\) \( \Leftrightarrow 2 = (m - 1).0 + m \Leftrightarrow m = 2\) Vậy với \(m = 2\) thì đồ thị của hàm số cắt trục tung tại điểm của tung độ bằng \(2\). Chọn B. Câu 2: Xác định giá trị của \(m\) để đồ thị của hàm số cắt hoành tại điểm có hoành độ bằng \( - 3\).
Đáp án: B Phương pháp giải: Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng \( - 3 \Rightarrow B\left( { - 3;\;0} \right)\) thuộc đồ thị hàm số. Thay tọa độ điểm B vào công thức hàm số ta tìm được giá trị của m. Lời giải chi tiết: Đồ thị của hàm số cắt trục hoành tại điểm của hoành độ bằng \( - 3\) nên đồ thị của hàm số đi qua điểm \(B( - 3\,;\,\,0)\) \(\begin{array}{l} \Leftrightarrow 0 = (m - 1).( - 3) + m \Leftrightarrow 0 = - 3m + 3 + m\\ \Leftrightarrow 2m = 3 \Leftrightarrow m = \frac{3}{2}\end{array}\) Vậy với \(m = \frac{3}{2}\) thì đồ thị của hàm số cắt trục hoành tại điểm của hoành độ bằng \( - 3\). Chọn B. Câu 3: Vẽ đồ thị của hai hàm số ứng với giá trị của \(m\) tìm được ở các câu 1) và 2) trên cùng hệ trục tọa độ \(Oxy\) và tìm tọa độ giao điểm của hai đường thẳng vừa vẽ được.
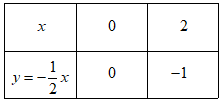
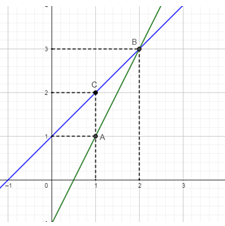
Đáp án: C Phương pháp giải: Lập bằng giá trị, vẽ đồ thị hàm số cả 2 đồ thị hàm số trên cùng hệ trục tọa độ. +) Lập phương trình hoành độ giao điểm của hai đồ thị hàm số để tìm hoành độ giao điểm của hai đồ thị hàm số. +) Thay hoành độ giao điểm vừa tìm được vào một trong hai công thức hàm số trên để tìm tung độ giao điểm của hai đồ thị. Lời giải chi tiết: +) Với \(m = 2\) hàm số trở thành \(y = x + 2\). +) Với \(m = \frac{3}{2}\) hàm số trở thành \(y = \frac{1}{2}x + \frac{3}{2}\). Ta có bảng giá trị: Đồ thị của hàm số \(y = x + 2\) là đường thẳng đi qua hai điểm \((1\,;\,\,3)\) và \((0\,;\,\,2)\). Đồ thị của hàm số \(y = \frac{1}{2}x + \frac{3}{2}\) là đường thẳng đi qua hai điểm \(\left( {0\,;\,\,\frac{3}{2}} \right)\) và \((1\,;\,\,2)\). +) Vẽ đồ thị của hai hàm số: +) Tìm tọa độ giao điểm của hai đồ thị hàm số. Hoành độ giao điểm của hai đồ thị hàm số là nghiệm của phương trình: \(\begin{array}{l}\;\;\;\;x + 2 = \frac{1}{2}x + \frac{3}{2} \Leftrightarrow x - \frac{1}{2}x = \frac{3}{2} - 2\\ \Leftrightarrow \frac{1}{2}x = \frac{{ - 1}}{2} \Leftrightarrow x = - 1\end{array}\) Với \(x = - 1\) ta được \(y = - 1 + 2 = 1\). Vậy tọa độ giao điểm của hai đường thẳng là \(( - 1\,;\,\,1)\). Chọn C. Câu hỏi 21 : Cho hàm số \(y = - \frac{1}{2}x\) có đồ thị \(\left( {{d_1}} \right)\) và hàm số \(y = x - 3\) có đồ thị \(\left( {{d_2}} \right)\). a) Vẽ \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) trên cùng hệ trục tọa độ b) Tìm tọa độ giao điểm A của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) bằng phép toán.
Đáp án: B Phương pháp giải: a) Nhận thấy hai hàm số \(y = - \frac{1}{2}x\) và \(y = x - 3\) là hai hàm bậc nhất, nên đồ thị của chúng là đường thẳng. Ta cần xác định hai điểm thuộc đồ thị, vẽ đường thẳng đi qua hai điểm đó là được đồ thị hàm số cần vẽ. b) Xác định hoành độ giao điểm bằng cách lập phương trình hoành độ giao điểm, từ đó tìm ra tọa độ của giao điểm. Lời giải chi tiết: a) Vẽ \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) trên cùng hệ trục tọa độ. +) Vẽ đường thẳng \({d_1}:\;\;y = - \frac{1}{2}x\) Vậy đồ thị hàm số \({d_1}:\;\;y = - \frac{1}{2}x\) là đường thẳng đi qua hai điểm \(\left( {0;\;0} \right),\;\left( { - 2;\; - 1} \right).\) +) Vẽ đường thẳng \({d_2}:\;\;y = x = - 3\) Vậy đồ thị hàm số \({d_2}:\;\;y = x - 3\) là đường thẳng đi qua hai điểm \(\left( {0;\; - 3} \right),\;\left( {3;\;0} \right).\) b) Tìm tọa độ giao điểm A của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) bằng phép toán. Hoành độ giao điểm của hai đường thẳng là nghiệm của phương trình: \( - \frac{1}{2}x = x - 3 \Leftrightarrow 3x = 6 \Leftrightarrow x = 2\) Với \(x = 2 \Rightarrow y = x - 3 = 2 - 3 = - 1\) Vậy giao điểm của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) là điểm \(A\left( {2; - 1} \right)\). Chọn B. Câu hỏi 22 : Cho đường thẳng \(\left( {{d_1}} \right):y = 2x - 1\) và đường thẳng \(\left( {{d_2}} \right):y = x + 1\) a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ. b) Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) bằng phép toán. Tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là:
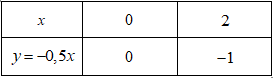
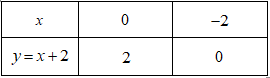
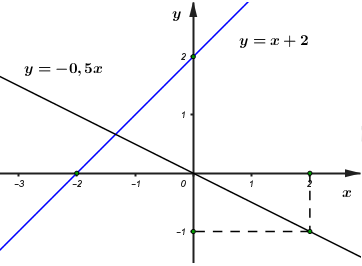
Đáp án: C Phương pháp giải: a) Nhận thấy \(\left( {{d_1}} \right):y = 2x - 1\) và \(\left( {{d_2}} \right):y = x + 1\) là hàm số bậc nhất, nên đồ thị hàm số của chúng là đường thẳng. Ta cần xác định 2 điểm nằm trên đồ thị hàm số. Đường thẳng đi qua hai điểm đó chính là đồ thị hàm số ta cần vẽ b) Để tìm tọa độ giao điểm, ta lập phương trình hoành độ giao điểm, từ đó tìm ra hoành độ của giao điểm, rồi tìm được giao điểm của hai đồ thị. Lời giải chi tiết: a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ. Ta có: +) Hai điểm \(A\left( {1;1} \right),B\left( {2;3} \right)\) thuộc đồ thị hàm số \(\left( {{d_1}} \right):y = 2x - 1\) +) Hai điểm \(B\left( {2;3} \right),C\left( {1;2} \right)\) thuộc đồ thị hàm số \(\left( {{d_2}} \right):y = x + 1\) Từ đó ta có đồ thị của hai hàm số: (hình bên) b) Hoành độ giao điểm là nghiệm của phương trình: \(2x - 1 = x + 1 \Leftrightarrow x = 2\) Với \(x = 2 \Rightarrow y = x + 1 = 3\) Vậy tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là \(B\left( {2;3} \right)\). Chọn C Câu hỏi 23 : Cho hàm số \(y = - 2x + 3\) có đồ thị là đường thẳng (d1) và hàm số \(y = 0,5x - 2\) có đồ thị là đường thẳng (d2) 1. Vẽ đường thẳng (d1) và (d2) trên cùng một mặt phẳng tọa độ 2. Tìm tọa độ giao điểm C của hai đường thẳng (d1) và (d2) bằng phép toán 3. Gọi A, B thứ tự là giao điểm của đường thẳng (d1) và (d2) với trục Oy. Tính diện tích tam giác ABC (đơn vị đo trên các trục tọa độ là cm)
Đáp án: B Phương pháp giải: 1. Lập bảng giá trị các điểm mà đồ thị hàm số đi qua sau đó vẽ đồ thị các hàm số đã cho. 2. Giải phương trình hoành độ giao điểm của 2 đồ thị hàm số ta tìm được hoành độ giao điểm. Thế hoành độ giao điểm đó vào một trong hai công thức hàm số của 2 đường thẳng đã cho ta tìm được tung độ của giao điểm. Từ đó ta có tọa độ giao điểm cần tìm 3. Tìm A, B, từ đó tính AB, CH (H là hình chiếu của C trên AB) để tính diện tích tam giác ABC. Lời giải chi tiết: Cho hàm số \(y = - 2x + 3\) có đồ thị là đường thẳng (d1) và hàm số \(y = 0,5x - 2\) có đồ thị là đường thẳng (d2) 1. Vẽ đường thẳng (d1) và (d2) trên cùng một mặt phẳng tọa độ +) Vẽ đồ thị hàm số \(y = - 2x + 3\) Vậy đồ thị hàm số \(y = - 2x + 3\) là đường thẳng \(\left( {{d_1}} \right)\) đi qua 2 điểm \(\left( {0;3} \right),\,\,\,\left( {1;1} \right)\) +) Vẽ đồ thị hàm số \(y = 0,5x - 2\) Vậy đồ thị hàm số \(y = 0,5x - 2\) là đường thẳng \(\left( {{d_2}} \right)\) đi qua 2 điểm \(\left( {0; - 2} \right),\,\,\,\left( {4;0} \right)\) 2. Tìm tọa độ giao điểm C của hai đường thẳng (d1) và (d2) bằng phép toán Hoành độ giao điểm C của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là nghiệm của phương trình: \(\begin{array}{l} - 2x + 3 = 0,5x - 2 \Leftrightarrow 2,5x = 5 \Leftrightarrow x = 2.\\ \Rightarrow y = - 2.2 + 3 = - 1.\end{array}\) Vậy tọa độ giao điểm của hai đường thẳng đã cho là: \(C\left( {2; - 1} \right).\) 3. Gọi A, B thứ tự là giao điểm của đường thẳng (d1) và (d2) với trục Oy. Tính diện tích tam giác ABC (đơn vị đo trên các trục tọa độ là cm) Gọi A, B thứ tự là giao điểm của đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\)với trục Oy. \(\begin{array}{l} \Rightarrow A\left( {0;\;{y_A}} \right);\;B\left( {0;\;{y_B}} \right)\\ \Rightarrow \left\{ \begin{array}{l}{y_A} = - 2.0 + 3 = 3\; \Rightarrow A\left( {0;\;3} \right)\\{y_B} = 0,5.0 - 2 = - 2 \Rightarrow B\left( {0; - 2} \right)\end{array} \right..\end{array}\) Ta có: \(AB = \left| {3 - \left( { - 2} \right)} \right| = 5\;cm.\) Gọi H là hình chiếu của C trên AB \( \Rightarrow CH \bot AB\) và \(CH = 2cm\) \( \Rightarrow {S_{\Delta ABC}} = \frac{1}{2}CH.AB = \frac{1}{2}.2.5 = 5\;\left( {c{m^2}} \right).\) Chọn B. Câu hỏi 24 : Cho hàm số \(y = \left( {m - 1} \right)x + 3\) có đồ thị là đường thẳng (d) 1) Vẽ đường thẳng (d) khi \(m = 2\) 2) Tìm m để đường thẳng (d) song song với đường thẳng \(y = 2x + 1\) 3) Tính khoảng cách từ gốc tọa độ đến đường thẳng được vẽ ở câu 1
Đáp án: A Phương pháp giải: 1) Thay \(m = 2\) vào phương trình đường thẳng \(\left( d \right)\) sau đó lập bảng giá trị và vẽ đồ thị hàm số. 2) Đường thẳng \(y = ax + b\) song song với đường thẳng \(y = a'x + b' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\) 3) Tìm giao điểm của \(y = x + 3\) với các trục Ox, Oy, sau đó sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách. Lời giải chi tiết: Cho hàm số \(y = \left( {m - 1} \right)x + 3\) có đồ thị là đường thẳng (d) 1) Vẽ đường thẳng (d) khi \(m = 2\) Khi \(m = 2\) thì (d): \(y = x + 3\) Ta có bảng giá trị: Vậy đồ thị hàm số \(\left( d \right)\;\;y = x + 3\) là đường thẳng đi qua 2 điểm \(\left( {0;3} \right),\left( { - 3;0} \right)\) 2) Tìm m để đường thẳng (d) song song với đường thẳng \(y = 2x + 1\) Để đường thẳng (d) song song với đường thẳng \(y = 2x + 1\) \( \Leftrightarrow \left\{ \begin{array}{l}m - 1 = 2\\3 \ne 1\end{array} \right. \Leftrightarrow m = 3\) Vậy với \(m = 3\) thỏa mãn yêu cầu đề bài. 3) Tính khoảng cách từ gốc tọa độ đến đường thẳng được vẽ ở câu 1 Gọi A, B lần lượt là giao điểm của đường thẳng \(y = x + 3\) với hai trục Ox, Oy \( \Rightarrow A\left( { - 3;0} \right),\,\,\,B\left( {0;3} \right) \Rightarrow OA = OB = 3\) Gọi H là hình chiếu của O trên AB. (như hình vẽ) Áp dụng hệ thức lượng trong tam giác OAB vuông cân tại O, đường cao OH ta có: \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} = \frac{1}{9} + \frac{1}{9} = \frac{2}{9} \Rightarrow O{H^2} = \frac{9}{2} \Rightarrow OH = \frac{{3\sqrt 2 }}{2}\;\;\;\left( {OH > 0} \right).\) Vậy khoảng cách từ gốc tọa độ đến \(\left( d \right):\;y = x + 3\) là \(OH = \frac{{3\sqrt 2 }}{2}.\) Chọn A. Câu hỏi 25 : Cho hàm số \(y = mx + 1\;\;\left( 1 \right)\) với \(m\) là tham số, \(m \ne 0.\) Câu 1: Tìm m để đồ thị hàm số (1) đi qua điểm \(M\left( { - 1; - 1} \right).\) Với m vừa tìm được, vẽ đồ thị hàm số (1) trên mặt phẳng tọa độ \(Oxy.\)
Đáp án: B Phương pháp giải: Thay tọa độ điểm \(M\left( { - 1; - 1} \right)\) vào công thức hàm số \(\left( 1 \right)\) để tìm m. +) Với giá trị m vừa tìm được, ta thay vào công thức hàm số và vẽ đồ thị hàm số trên mặt phẳng tọa độ. Lời giải chi tiết: Đồ thị hàm số \(\left( 1 \right)\) đi qua điểm \(M\left( { - 1; - 1} \right)\) nên ta có: \( - 1 = m\left( { - 1} \right) + 1 \Leftrightarrow m = 2\;\;\left( {tm} \right)\) Vậy với \(m = 2\) thì đồ thị hàm số đã cho đi qua điểm \(M\left( { - 1; - 1} \right).\) Với \(m = 2\) ta có: \(y = 2x + 1.\) Ta có bảng giá trị: Vậy đồ thị hàm số \(y = 2x + 1\) là đường thẳng đi qua hai điểm \(\left( {0;\;1} \right),\;\left( { - 1; - 1} \right).\) Chọn B. Câu 2: Tìm m để đồ thị hàm số (1) song song với đường thẳng \(\left( d \right):\;y = \left( {{m^2} - 2} \right)x + 2m + 3.\)
Đáp án: C Phương pháp giải: Hai đường thẳng \({d_1}:\;\;y = {a_1}x + {b_1}\) và \({d_2}:\;y = {a_2}x + {b_2}\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\) Lời giải chi tiết: Điều kiện \(m \ne 0.\) Đường thẳng \(y = mx + 1\;\;\left( 1 \right)\) song song với đường thẳng \(\left( d \right):\;y = \left( {{m^2} - 2} \right)x + 2m + 3\) \( \Leftrightarrow \left\{ \begin{array}{l}m = {m^2} - 2\\2m + 3 \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - m - 2 = 0\\2m \ne - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = - 1\\m = 2\end{array} \right.\\m \ne - 1\end{array} \right. \Leftrightarrow m = 2\;\;\left( {tm} \right)\) Vậy \(m = 2\) thỏa mãn điều kiện bài toán. Chọn C. Câu 3: Tìm m để khoảng cách từ gốc tọa độ O đến đồ thị hàm số (1) bằng \(\frac{2}{{\sqrt 5 }}.\)
Đáp án: C Phương pháp giải: Gọi H là hình chiếu của O trên đường thẳng \(\left( 1 \right).\) Khi đó áp dụng hệ thức lượng trong tam giác vuông để tính độ dài OH. Lời giải chi tiết: Điều kiện \(m \ne 0.\) Gọi \(A,\;B\) lần lượt là các giao điểm của đường thẳng \(\left( 1 \right)\) với các trục \(Ox,\;Oy.\) Khi đó ta có: \(A\left( {{x_1};\;0} \right),\;\;B\left( {0;\;{y_2}} \right).\) \( \Rightarrow \left\{ \begin{array}{l}0 = m{x_1} + 1\\m.0 + 1 = {y_2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} = - \frac{1}{m}\\{y_2} = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}A\left( { - \frac{1}{m};\;0} \right)\\B\left( {0;\;1} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}OA = \left| { - \frac{1}{m}} \right| = \frac{1}{{\left| m \right|}}\\OB = \left| 1 \right| = 1\end{array} \right..\) Gọi \(H\) là hình chiếu của \(O\) trên đường thẳng \(\left( 1 \right) \Rightarrow OH = \frac{2}{{\sqrt 5 }}.\) Khi đó ta có \(\Delta AOB\) vuông tại \(O\) và có đường cao \(OH.\) Áp dụng hệ thức lượng cho \(\Delta AOB\) vuông tại \(O\) và có đường cao \(OH\) ta có: \(\begin{array}{l}\;\;\;\;\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} \Leftrightarrow \frac{1}{{{{\left( {\frac{2}{{\sqrt 5 }}} \right)}^2}}} = \frac{1}{{{{\left| {{x_1}} \right|}^2}}} + \frac{1}{{{{\left| {{y_2}} \right|}^2}}}\\ \Leftrightarrow \frac{5}{4} = \frac{1}{{{{\left( { - \frac{1}{m}} \right)}^2}}} + \frac{1}{{{1^2}}} \Leftrightarrow \frac{5}{4} = {m^2} + 1\\ \Leftrightarrow 5 = 4{m^2} + 4 \Leftrightarrow 4{m^2} = 1 \Leftrightarrow {m^2} = \frac{1}{4} \Leftrightarrow m = \pm \frac{1}{2}\;\left( {tm} \right)\end{array}\) Vậy \(m = \pm \frac{1}{2}\) thỏa mãn điều kiện bài toán. Chọn C. Câu hỏi 26 : Chọn đáp án đúng nhất: Câu 1: Cho đường thẳng \(\left( d \right):\,\,y = ax + b\). Tìm \(a,\,\,b\) để đường thẳng \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right):\,\,y = 5x + 6\) và đi qua điểm \(A\left( {2;3} \right)\).
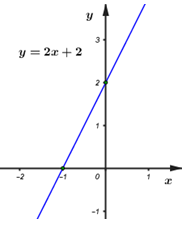
Đáp án: C Phương pháp giải: Hai đường thẳng \(d:\,\,y = {a_1}x + {b_1},\,\,\,d':\,\,y = {a_2}x + {b_2}\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\) Sau đó thay tọa độ điểm A vào công thức hàm số \(\left( d \right).\) Lời giải chi tiết: Ta có: \(\left( d \right):\,\,y = ax + b\) song song với đường thẳng \(\left( {d'} \right):\,\,y = 5x + 6 \Rightarrow \left\{ \begin{array}{l}a = 5\\b \ne 6\end{array} \right. \Rightarrow \left( d \right):\,\,y = 5x + b\,\,\,\,\left( {b \ne 6} \right).\) Đường thẳng \(\left( d \right)\) đi qua điểm \(A\left( {2;3} \right)\) nên thay tọa độ điểm \(A\) vào phương trình đường thẳng \(\left( d \right)\) ta được: \(3 = 5.2 + b \Leftrightarrow b = - 7\,\,\,\left( {tm} \right)\) Vậy phương trình đường thẳng \(\left( {d'} \right):\,\,\,y = 5x - 7.\) Chọn C. Câu 2: Giải hệ phương trình \(\left\{ \begin{array}{l}3x + 2y = 11\\x + 2y = 5\end{array} \right.\).
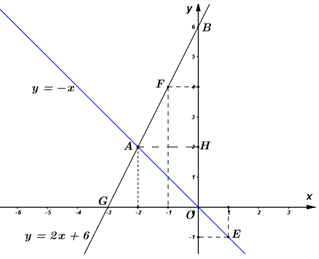
Đáp án: B Phương pháp giải: Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số. Lời giải chi tiết: \(\left\{ \begin{array}{l}3x + 2y = 11\\x + 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x = 6\\x + 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\3 + 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\2y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 1\end{array} \right.\). Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {3;1} \right)\). Chọn B. Câu hỏi 27 : Trong mặt phẳng tọa độ \(Oxy,\) cho đường thẳng \(\left( d \right):y = 2x - 4\). 1) Xác định tọa độ các giao điểm \(A,\,\,B\) của \(\left( d \right)\) với hai trục \(Ox,\,\,Oy.\) Vẽ \(\left( d \right)\) trong mặt phẳng tọa độ Oxy. 2) Tính chu vi và diện tích tam giác \(OAB\). 3) Tìm \(m\) để đường thẳng \(\left( {{d_m}} \right):y = \left( {{m^2} - 2} \right)x + 2m - 2{m^2}\) song song với \(\left( d \right)\). Phương pháp giải: 1) Vẽ đường thẳng trong mặt phẳng Oxy bằng cách xác định hai điểm mà đường thẳng đi qua. 2) Áp dụng định lý Pytago trong tam giác vuông để tính các cạnh của tam giác. 3) Đường thẳng \(y = ax + b\) song song với đường thẳng \(y = a'x + b' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\) Lời giải chi tiết: Cho đường thẳng \(\left( d \right):y = 2x - 4\). 1) Xác định tọa độ các giao điểm A, B của \(\left( d \right)\) với hai trục Ox, Oy. Vẽ \(\left( d \right)\) trong mặt phẳng tọa độ Oxy. +) Giao điểm \(A\) của đường thẳng \(\left( d \right)\) với trục \(Ox\) là: \({y_A} = 0 \Rightarrow 2{x_A} - 4 = 0\, \Rightarrow {x_A} = 2\, \Rightarrow A\left( {2;0} \right)\) +) Giao điểm \(B\) của đường thẳng \(\left( d \right)\) với trục \(Oy\) là: \({x_B} = 0 \Rightarrow {y_B} = 2{x_B} - 4 = - 4\, \Rightarrow B\left( {0; - 4} \right)\) +) Vẽ đường thẳng \(\left( d \right)\) trong mặt phẳng \(Oxy:\) Ta có đường thẳng \(\left( d \right)\) đi qua hai điểm \(A\left( {2;0} \right);B\left( {0; - 4} \right)\) nên đường thẳng \(\left( d \right)\) chính là đường thẳng \(AB.\) Ta có hình vẽ: 2) Tính chu vi và diện tích tam giác \(OAB\). Từ hình vẽ ta thấy \(\Delta OAB\) vuông tại \(O,\,\,OA = 2,\,\,OB = 4\) (đvđd) Áp dụng định lý Pitago cho tam giác \(OAB\) vuông tại \(O\) ta có: \(AB = \sqrt {O{A^2} + O{B^2}} = \sqrt {{2^2} + {4^2}} = \sqrt {20} = 2\sqrt 5 \,\) (đvđd) Chu vi \(\Delta OAB\) là: \({C_{AOB}} = OA + OB + AB = 2 + 4 + 2\sqrt 5 = 6 + 2\sqrt 5 \,\)(đvđd) Diện tích \(\Delta OAB\):\({S_{OAB}} = \frac{1}{2}.OA.OB = \frac{1}{2}.2.4 = 4\) (đvdt) Vậy chu vi và diện tích tam giác \(OAB\) lần lượt là \(6 + 2\sqrt 5 \) (đvđd) và \(4\)(đvdt). 3) Tìm \(m\) để đường thẳng \(\left( {{d_m}} \right):y = \left( {{m^2} - 2} \right)x + 2m - 2{m^2}\) song song với \(\left( d \right)\). Để đường thẳng \(\left( {{d_m}} \right):y = \left( {{m^2} - 2} \right)x + 2m - 2{m^2}\) song song với \(\left( d \right)\) thì: \(\begin{array}{l}\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{m^2} - 2 = 2\\2m - 2{m^2} \ne - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} = 4\\2{m^2} - 2m - 4 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} = 4\\{m^2} - m - 2 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 2\\m = - 2\end{array} \right.\\\left( {m - 2} \right)\left( {m + 1} \right) \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 2\\m = - 2\end{array} \right.\\m \ne 2\\m \ne - 1\end{array} \right. \Leftrightarrow m = - 2\end{array}\) Vậy \(m = - 2\) thì thỏa mãn yêu cầu. Câu hỏi 28 : Cho hai hàm số \(y = - x\) và \(y = 2x + 6\). a) Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ. b) Gọi \(A\) là giao điểm của hai đồ thị nói trên. Tìm tọa độ điểm \(A.\) c) Gọi \(B\) là giao điểm của đồ thị hàm số \(y = 2x + 6\) với trục tung. Tính diện tích của tam giác \(OAB\) (với \(O\) là gốc tọa độ và đơn vị trên các trục tọa độ là xentimet).
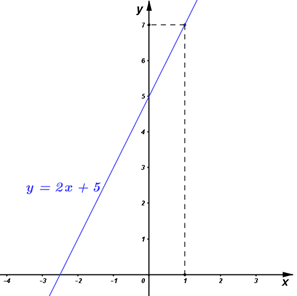
Đáp án: C Phương pháp giải: a) Lập bảng giá trị các điểm mà đồ thị hàm số đi qua sau đó vẽ đồ thị các hàm số đã cho. b) Giải phương trình hoành độ giao điểm của 2 đồ thị hàm số ta tìm được hoành độ giao điểm. Thế hoành độ giao điểm đó vào một trong hai công thức hàm số của 2 đường thẳng đã cho ta tìm được tung độ của giao điểm. Từ đó ta có tọa độ giao điểm cần tìm c) Tính OB, AH (H là hình chiếu của A trên OB) để tính diện tích tam giác OAB. Lời giải chi tiết: a) Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ. Ta có bảng giá trị của hai hàm số: Đồ thị hàm số \(y = - x\) là đường thẳng đi qua hai điểm \(O\left( {0;0} \right);E\left( {1; - 1} \right)\) Đồ thị hàm số \(y = 2x + 6\) là đường thẳng đi qua hai điểm \(F\left( { - 1;4} \right);\,G\left( { - 3;0} \right)\) b) Gọi \(A\) là giao điểm của hai đồ thị nói trên. Tìm tọa độ điểm \(A.\) Xét phương trình hoành độ giao điểm của hai hàm số: \(y = - x\) và \(y = 2x + 6\) ta có: \( - x = 2x + 6\,\,\, \Rightarrow - 3x = 6\,\,\, \Rightarrow x = - 2\) Thay \(x = - 2\) vào phương trình: \(y = - x\) ta được \(y = 2\). Vậy giao điểm \(A\) của hai đồ thị hàm số có tọa độ là \(A\left( { - 2;2} \right)\). c) Gọi \(B\) là giao điểm của đồ thị hàm số \(y = 2x + 6\) với trục tung. Tính diện tích của tam giác \(OAB\) (với \(O\) là gốc tọa độ và đơn vị trên các trục tọa độ là xentimet). Ta có \(B\) là giao điểm của đồ thị hàm số \(y = 2x + 6\) với trục tung nên \({x_B} = 0 \Rightarrow {y_B} = 2{x_B} + 6 = 6\, \Rightarrow B\left( {0;6} \right)\) \( \Rightarrow OB = 6\,\,\,\left( {cm} \right)\) Gọi \(H\) là hình chiếu của \(A\) trên \(Oy,\) khi đó ta sẽ có: \(AH \bot OB = \left\{ H \right\}\) và \(AH = \left| {{x_A}} \right| = 2\,\,\,\left( {cm} \right)\) Suy ra \({S_{OAB}} = \frac{1}{2}.AH.OB = \frac{1}{2}.2.6 = 6\,\,\,\,\left( {c{m^2}} \right)\) Vậy diện tích tam giác \(OAB\) là \(6\,\,c{m^2}\). Chọn C. Câu hỏi 29 : 1) Vẽ đồ thị hàm số \(y = 2x + 5\,\,\left( d \right)\). 2) Tìm tọa độ giao điểm của đường thẳng \(\left( \Delta \right):y = - x - 4\) với \(\left( d \right)\).
Đáp án: A Phương pháp giải: 1) Lập bảng giá trị các điểm mà đồ thị hàm số đi qua sau đó vẽ đồ thị các hàm số đã cho. 2) Giải phương trình hoành độ giao điểm của 2 đồ thị hàm số ta tìm được hoành độ giao điểm. Thế hoành độ giao điểm đó vào một trong hai công thức hàm số của 2 đường thẳng đã cho ta tìm được tung độ của giao điểm. Từ đó ta có tọa độ giao điểm cần tìm. Lời giải chi tiết: 1) Vẽ đồ thị hàm số \(y = 2x + 5\,\,\left( d \right)\). Ta có bảng giá trị: Vậy đồ thị hàm số \(y = 2x + 5\,\,\left( d \right)\) là đường thẳng đi qua 2 điểm \(\left( {0;5} \right);\,\,\left( {1;7} \right).\) 2) Tìm tọa độ giao điểm của đường thẳng \(\left( \Delta \right):y = - x - 4\) với \(\left( d \right)\). Xét phương trình hoành độ giao điểm của \(\left( \Delta \right)\) và \(\left( d \right)\): \(2x + 5 = - x - 4 \Rightarrow 3x = - 9 \Rightarrow x = - 3\) \( \Rightarrow y = 2x + 5 = 2.\left( { - 3} \right) + 5 = - 1\) Vậy tọa độ giao điểm của \(\left( \Delta \right)\) và \(\left( d \right)\) là \(\left( { - 3; - 1} \right)\). Chọn A. Câu hỏi 30 : Cho hàm số \(y = \left( {2 - m} \right)x + 2\) với m là tham số và \(m \ne 2\), có đồ thị là đường thẳng \(d.\) 1) Vẽ đồ thị của hàm số trên với \(m = 3\). 2) Xác định giá trị của \(m\) để đường thẳng \(d\) cắt đường thẳng \(y = 2x - 4\) tại một điểm nằm trên trục hoành.
Đáp án: C Phương pháp giải: 1) Thay \(m = 3\)thỏa mãn điều kiện vào hàm số, lập bảng giá trị và vẽ đồ thị hàm số. 2) Tìm giao điểm của đường thẳng \(y = 2x - 4\)với trục hoành, giao điểm của đồ thị hàm số chính là điểm vừa tìm, từ đó thay tọa độ của điểm vào phương trình d để tìm \(m.\) Lời giải chi tiết: 1) Vẽ đồ thị của hàm số trên với \(m = 3\). Thay \(m = 3\) vào hàm số đã cho ta được: \(y = \left( {2 - 3} \right)x + 2 \Rightarrow y = - x + 2\) Ta có bảng giá trị của d: Vậy với \(m = 3\) thì đồ thị hàm số là đường thẳng đi qua hai điểm \(\left( {0;\,\,2} \right);\left( {1;\,\,1} \right).\) 2) Xác định giá trị của \(m\) để đường thẳng \(d\) cắt đường thẳng \(y = 2x - 4\) tại một điểm nằm trên trục hoành. Gọi \(M\left( {{x_0};\,\,0} \right)\) là giao điểm của đồ thị đường thẳng \(y = 2x - 4\) và trục \(Ox.\) \( \Rightarrow 0 = 2{x_0} - 4 \Leftrightarrow {x_0} = 2 \Rightarrow M\left( {2;\,\,0} \right).\) Lại có \(d\) cắt đường thẳng \(y = 2x - 4\) tại\(M\left( {2;\,\,0} \right)\) \( \Rightarrow 0 = \left( {2 - m} \right).2 + 2 \Leftrightarrow 2 - m = - 1 \Leftrightarrow m = 3\,\,\,\,\left( {tm} \right).\) Vậy \(m = 3\). Chọn C. Câu hỏi 31 : 1) Cho hai hàm số \(y = 2x + 5\) và \(y = - 3x\) có đồ thị lần lượt là \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\). Vẽ hai đồ thị \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ. 2) Cho hàm số \(y = \left( {m - 1} \right)x + 6\) có đồ thị là \(\left( {{d_3}} \right)\), với \(m\) là tham số thực. - Tìm các giá trị của \(m\) để \(\left( {{d_3}} \right)\) song song với \(\left( {{d_1}} \right)\). - Tìm các giá trị của \(m\) để \(\left( {{d_3}} \right)\)cắt \(\left( {{d_2}} \right)\). Phương pháp giải: 1) Lập bảng giá trị và vẽ đồ thị hàm số 2) Hai đường thẳng có phương trình \(y = ax + b;y = a'x + b'\): - Song song nhau khi: \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\) - Cắt nhau khi \(a \ne a'\) - Vuông góc khi: \(a.a' = - 1\) - Trùng nhau khi: \(\left\{ \begin{array}{l}a = a'\\b = b'\end{array} \right.\) Lời giải chi tiết: 1) Cho hai hàm số \(y = 2x + 5\) và \(y = - 3x\) có đồ thị lần lượt là \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\). Vẽ hai đồ thị \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ. +) Ta có bảng giá trị của hàm số \(y = 2x + 5\): Đồ thị hàm số \(y = 2x + 5\) là đường thẳng đi qua hai điểm \(\left( {0;5} \right)\)và \(\left( { - 1;3} \right)\) +) Ta có bảng giá trị của hàm số \(y = - 3x\): Đồ thị hàm số \(y = - 3x\) là đường thẳng đi qua gốc tọa độ và điểm \(\left( { - 1;3} \right)\)
2) Cho hàm số \(y = \left( {m - 1} \right)x + 6\) có đồ thị là \(\left( {{d_3}} \right)\), với \(m\) là tham số thực. - Tìm các giá trị của \(m\) để \(\left( {{d_3}} \right)\) song song với \(\left( {{d_1}} \right)\). Để \(\left( {{d_3}} \right)\) song song với \(\left( {{d_1}} \right)\) thì: \(\left\{ \begin{array}{l} - Tìm các giá trị của \(m\) để \(\left( {{d_3}} \right)\) cắt \(\left( {{d_2}} \right)\). Để \(\left( {{d_3}} \right)\)cắt \(\left( {{d_2}} \right)\) thì: \(a \ne a' \Leftrightarrow m - 1 \ne - 3 \Leftrightarrow m \ne - 2\) Vậy \(\left( {{d_3}} \right)\) song song với \(\left( {{d_1}} \right)\)khi \(m = 3\)và \(\left( {{d_3}} \right)\)cắt \(\left( {{d_2}} \right)\) khi \(m \ne - 2\). Câu hỏi 32 : Cho hai đường thẳng \({d_1}:y = \left( {m - 2} \right)x + m + 4\) và \({d_2}:y = \left( {n + 1} \right)x - 3\) Câu 1: Tìm điều kiện của \(m\) để hàm số có đồ thị \({d_1}\) luôn nghịch biến và điều kiện của \(n\) để hàm số có đồ thị \({d_2}\) luôn đồng biến.
Đáp án: C Phương pháp giải: Hàm số có phương trình \(y = ax + b\left( {a \ne 0} \right)\): Luôn đồng biến khi \(a > 0\)và nghịch biến khi \(a < 0.\) Lời giải chi tiết: Hàm số có đồ thị \({d_1}:y = \left( {m - 2} \right)x + m + 4\) luôn nghịch biến \( \Leftrightarrow m - 2 < 0 \Leftrightarrow m < 2\) Hàm số có đồ thị \({d_2}:y = \left( {n + 1} \right)x - 3\) luôn đồng biến \( \Leftrightarrow n + 1 > 0 \Rightarrow n > - 1\) Vậy \(m < 2\) thì hàm số có đồ thị \({d_1}\) luôn nghịch biến. \(n > - 1\) thì hàm số có đồ thị \({d_2}\)luôn đồng biến. Chọn C. Câu 2: Tìm các giá trị của \(m\) và của \(n\) để hai đường thẳng \({d_1}\)và \({d_2}\) cùng đi qua điểm \(A\left( {1;0} \right).\)
Đáp án: A Phương pháp giải: Hai đường thẳng cùng đi qua 1 điểm thì tọa độ của điểm đó đều thỏa mãn hai phương trình đường thẳng. Lời giải chi tiết: Hai đường thẳng \({d_1}\)và \({d_2}\) cùng đi qua điểm \(A\left( {1;0} \right)\) nên ta thay tọa độ điểm A vào hai phương trình ta được: \(\left\{ \begin{array}{l}0 = \left( {m - 2} \right).1 + m + 4\\0 = \left( {n + 1} \right).1 - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m - 2 + m + 4 = 0\\n + 1 - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2m = - 2\\n = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = - 1\\n = 2\end{array} \right.\) Vậy \(m = - 1;n = 2\). Chọn A. Câu hỏi 33 : Trên mặt phẳng tọa độ \(Oxy\) cho hai điểm \(A,\,\,B\) như hình bên.
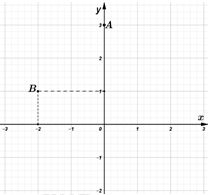
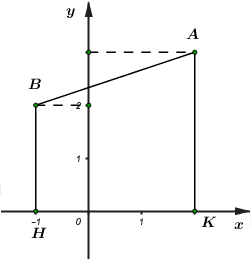
Câu 1: Hãy xác định tọa độ của hai điểm \(A,\,\,B.\)
Đáp án: D Phương pháp giải: Dựa vào đồ thị hàm số suy ra tọa độ các điểm \(A,\,\,B.\) Lời giải chi tiết: Dựa vào đồ thị hàm số ta xác định được: \(A\left( {0;3} \right)\) và \(B\left( { - 2;1} \right).\) Chọn D. Câu 2: Viết phương trình đường thẳng \(\left( d \right)\) đi qua hai điểm \(A,\,\,B.\)
Đáp án: C Phương pháp giải: Viết phương trình đường thẳng đi qua hai điểm đã cho bằng cách gọi phương trình tổng quát \(y = ax + b\) và thay tọa độ từng điểm vào phương trình để tìm \(a,\,\,b.\) Lời giải chi tiết: Gọi phương trình đường thẳng \(\left( d \right)\) đi qua hai điểm \(A\) và \(B\) có dạng : \(y = ax + b\) Do \(A \in \left( d \right);\,\,\,B \in \left( d \right)\) nên thay tọa độ hai điểm vào phương trình, ta được: \(\left\{ \begin{array}{l}3 = a.0 + b\\1 = a.\left( { - 2} \right) + b\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b = 3\\ - 2a = 1 - b\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b = 3\\ - 2a = 1 - 3 = - 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b = 3\\a = 1\end{array} \right.\)\( \Rightarrow \left( d \right):y = x + 3\) Vậy \(\left( d \right):y = x + 3\). Chọn C. Câu hỏi 34 : a) Vẽ đồ thị hàm số sau trên cùng một mặt phẳng tọa độ: \(\left( {{d_1}} \right):y = 2x - 3\) và \(\left( {{d_2}} \right):y = - \frac{1}{2}x + 2\) b) Tìm tọa độ giao điểm \(A\) của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) (bằng phép tính) c) Tìm \(m\) để ba đường thẳng \(\left( {{d_1}} \right)\), \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right):y = 3x - 2m - 3\) đồng quy.
Đáp án: A Phương pháp giải: a) Lập bảng giá trị của hai hàm số và vẽ chúng trên cùng 1 mặt phẳng tọa độ b) Xét phương trình hoành độ giao điểm của hai đồ thị để tìm \(x,\) thay giá trị \(x\) vừa tìm được vào 1 trong hai phương trình để tìm \(y.\) c) 3 đường thẳng đồng quy khi và chỉ khi đường thẳng thứ ba đi qua giao điểm của hai đường thẳng còn lại. Lời giải chi tiết: a) Vẽ đồ thị hàm số sau trên cùng một mặt phẳng tọa độ: \(\left( {{d_1}} \right):y = 2x - 3\) và \(\left( {{d_2}} \right):y = - \frac{1}{2}x + 2\) +) Vẽ đồ thị hàm số \(\left( {{d_1}} \right):y = 2x - 3\): Bảng giá trị: Vậy đồ thị hàm số \(\left( {{d_1}} \right)\) là đường thẳng đi qua hai điểm \(\left( {1; - 1} \right);\left( {3;3} \right)\) +) Vẽ đồ thị hàm số \(\left( {{d_2}} \right):y = - \frac{1}{2}x + 2\) Bảng giá trị: Vậy đồ thị hàm số \(\left( {{d_2}} \right)\) là đường thẳng đi qua hai điểm \(\left( {0;2} \right);\left( {4;0} b) Tìm tọa độ giao điểm \(A\) của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) (bằng phép tính). Xét phương trình hoành độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\): \(2x - 3 = - \frac{1}{2}x + 2 \Leftrightarrow 2x + \frac{1}{2}x = 2 + 3 \Leftrightarrow \frac{5}{2}x = 5 \Leftrightarrow x = 2\) Thay \(x = 2\) vào hàm số \(y = 2x - 3\) ta được \(y = 2.2 - 3 = 1.\) Vậy tọa độ giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là \(A\left( {2;1} \right)\). c) Tìm \(m\) để ba đường thẳng \(\left( {{d_1}} \right)\), \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right):y = 3x - 2m - 3\) đồng quy. Ba đường thẳng \(\left( {{d_1}} \right)\) , \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right):y = 3x - 2m - 3\) đồng quy \( \Rightarrow \left( {{d_3}} \right)\) đi qua giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\)\( \Rightarrow A \in \left( {{d_3}} \right)\) Thay tọa độ điểm \(A\) vào hàm số \(\left( {{d_3}} \right):\,\,y = 3x - 2m - 3\) ta được: \(1 = 3.2 - 2m - 3\)\( \Rightarrow 2m = 6 - 3 - 1 \Rightarrow m = 1\) Vậy \(m = 1\) thì ba đường thẳng \(\left( {{d_1}} \right)\) , \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right):y = 3x - 2m - 3\) đồng quy. Chọn A. Câu hỏi 35 : Trong mặt phẳng tọa độ \(Oxy,\) cho đường thẳng \(\left( {{d_m}} \right):y = mx - 2\)\(\left( {m \ne 0} \right)\) Câu 1: Xác định \(m\) để hàm số \(y = mx - 2\)\(\left( {m \ne 0} \right)\) đồng biến.
Đáp án: A Phương pháp giải: Hàm số \(y = ax + b\,\,\,\left( {a \ne 0} \right)\)đồng biến khi \(a > 0\) và nghịch biến khi \(a < 0\). Lời giải chi tiết: Hàm số \(y = mx - 2\) đồng biến\( \Leftrightarrow m > 0\) Vậy \(m > 0.\) Chọn A. Câu 2: Xác định giá trị của \(m\) để đường thẳng \(\left( {{d_m}} \right)\) đi qua điểm \(A\left( {1;2} \right)\). Vẽ đồ thị ứng với \(m\) tìm được.
Đáp án: D Phương pháp giải: Một điểm thuộc 1 đường thẳng khi tọa độ điểm đó thỏa mãn phương trình đường thẳng. Vẽ đồ thị hàm số bằng cách lập bảng giá trị. Lời giải chi tiết: Đường thẳng \(\left( {{d_m}} \right)\) đi qua điểm \(A\left( {1;2} \right)\) nên ta thay tọa độ điểm \(A\) vào phương trình đường thẳng \(\left( {{d_m}} \right)\)ta được: \(2 = m.1 - 2 \Rightarrow m = 4\) Khi \(m = 4\) đường thẳng có phương trình \(y = 4x - 2\), ta có bảng giá trị: Vậy đồ thị hàm số khi \(m = 4\) chính là đường thẳng đi qua hai điểm\(B\left( {0; - 2} \right)\) và \(A\left( {1;2} \right)\) Câu 3: Xác định giá trị của \(m\) để đường thẳng \(\left( {{d_m}} \right)\) cắt hai trục tọa độ tạo thành tam giác có diện tích bằng \(1.\)
Đáp án: D Phương pháp giải: Tìm giao điểm của đường thẳng và 2 trục tọa độ, tam giác tạo thành là tam giác vuông. Lời giải chi tiết: Điều kiện: \(m \ne 0.\) +) Với \(y = 0 \Rightarrow mx - 2 = 0 \Rightarrow mx = 2 \Rightarrow x = \frac{2}{m}\) \( \Rightarrow \left( {{d_m}} \right):y = mx - 2\) với cắt \(Ox\) tại điểm \(A\left( {\frac{2}{m};\,\,0} \right).\) +) Với \(x = 0 \Rightarrow y = - 2 \Rightarrow B\left( {0;\,\, - 2} \right)\) là giao của \(\left( {{d_m}} \right)\) và \(Oy.\) Khi đó diện tích của tam giác sẽ là: \(\begin{array}{l}{S_{OAB}} = \frac{1}{2}OA.OB = \frac{1}{2}.\left| {\frac{2}{m}} \right|.\left| { - 2} \right| = \frac{2}{{\left| m \right|}} = 1\\ \Leftrightarrow \left| m \right| = 2 \Leftrightarrow \left[ \begin{array}{l}m = 2\\m = - 2\end{array} \right..\end{array}\) Vậy \(m = 2\)hoặc \(m = - 2\)thì đường thẳng \(\left( {{d_m}} \right)\) cắt hai trục tọa độ tạo thành tam giác có diện tích bằng 1. Chọn D. Câu hỏi 36 : Cho hàm số \(y = \left( {m + 1} \right)x + 6\,\,\,\left( 1 \right)\) với \(m \ne - 1\) 1) Vẽ đồ thị hàm số \(\left( 1 \right)\) khi \(m = 2.\) 2) Gọi đồ thị của hàm số \(\left( 1 \right)\) là đường thẳng \(\left( d \right),\) tìm \(m\) để đường thẳng \(\left( d \right)\) cắt đường thẳng \(y = 5x + m - 2\) tại một điểm nằm trên trục tung. 3) Tìm \(m\) để khoảng cách từ gốc tọa độ \(O\) đến đường thẳng \(\left( d \right)\) bằng \(3\sqrt 2 .\)
Đáp án: C Phương pháp giải: 1) Vẽ đường thẳng trong mặt phẳng Oxy bằng cách xác định hai điểm mà đường thẳng đi qua. 2) Để hai đường thẳng \(\left( d \right):y = ax + b\) và \(\left( {d'} \right):y = a'x + b'\) cắt nhau tại một điểm trên trục tung thì \(a \ne a'\) và phương trình hoành độ giao điểm của hai đường thẳng có nghiệm \(x = 0\). 3) Tìm tọa độ giao điểm của đồ thị hàm số với trục hoành và trục tung. Sau đó sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách. Lời giải chi tiết: 1) Vẽ đồ thị hàm số \(\left( 1 \right)\) khi \(m = 2.\) Với \(m = 2\) thì \(y = 3x + 6\) Vẽ đồ thị hàm số: \(y = 3x + 6:\) +) Giao điểm \(A\) của đường thẳng \(y = 3x + 6\) với trục \(Ox\) là: \({y_A} = 0 \Rightarrow 3{x_A} + 6 = 0\, \Rightarrow {x_A} = - 2\, \Rightarrow A\left( { - 2;0} \right)\) +) Giao điểm \(B\) của đường thẳng \(y = 3x + 6\) với trục \(Oy\) là: \({x_B} = 0 \Rightarrow {y_B} = 3{x_B} + 6 = 6\, \Rightarrow B\left( {0;6} \right)\) +) Vẽ đường thẳng \(y = 3x + 6\) trong mặt phẳng \(Oxy:\) Ta có đường thẳng \(y = 3x + 6\) đi qua hai điểm \(A\left( { - 2;0} \right);B\left( {0;6} \right)\) nên đường thẳng \(y = 3x + 6\) chính là đường thẳng \(AB.\) Ta có hình vẽ bên. 2) Gọi đồ thị của hàm số \(\left( 1 \right)\) là đường thẳng \(\left( d \right),\) tìm \(m\) để đường thẳng \(\left( d \right)\) cắt đường thẳng \(y = 5x + m - 2\) tại một điểm nằm trên trục tung. Để \(d:\,\,y = \left( {m + 1} \right)x + 6\) cắt đường thẳng \(y = 5x + m - 2\) tại một điểm nằm trên trục tung thì \(m + 1 \ne 5\) và phương trình hoành độ giao điểm của hai đường thẳng có nghiệm \(x = 0\) \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}m + 1 \ne 5\\\left( {m + 1} \right).0 + 6 = 5.0 + m - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 4\\6 = m - 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 4\\m = 8\end{array} \right. \Leftrightarrow m = 8\,\,\,\left( {tmdk\,\,m \ne - 1} \right)\end{array}\) Vậy \(m = 8\) là giá trị cần tìm. 3) Tìm \(m\) để khoảng cách từ gốc tọa độ \(O\) đến đường thẳng \(\left( d \right)\) bằng \(3\sqrt 2 .\) Đồ thị hàm số \(y = \left( {m + 1} \right)x + 6\) với \(m \ne - 1\) là đường thẳng cắt \(Ox\) tại điểm \(A'\left( { - \frac{6}{{m + 1}};0} \right)\) và cắt \(Oy\) tại điểm \(B\left( {0;6} \right)\) Suy ra: \(OA' = \left| {\frac{{ - 6}}{{m + 1}}} \right| = \frac{6}{{\left| {m + 1} \right|}}\) và \(OB = \left| 6 \right| = 6\) Kẻ \(OH \bot A'B\) tại \(H\) thì \(OH\) chính là khoảng cách từ \(O\) đến đường thẳng \(\left( d \right)\) Ta có: \(\begin{array}{l}\frac{1}{{O{H^2}}} = \frac{1}{{OA{'^2}}} + \frac{1}{{O{B^2}}} \Leftrightarrow \frac{1}{{{{\left( {3\sqrt 2 } \right)}^2}}} = \frac{1}{{{{\left( {\frac{6}{{\left| {m + 1} \right|}}} \right)}^2}}} = \frac{1}{{{6^2}}}\\ \Leftrightarrow \frac{1}{{16}} = \frac{1}{{\frac{{36}}{{{{\left( {m + 1} \right)}^2}}}}} + \frac{1}{{36}} \Leftrightarrow \frac{1}{{18}} = \frac{{{{\left( {m + 1} \right)}^2} + 1}}{{36}}\\ \Leftrightarrow \frac{2}{{36}} = \frac{{{m^2} + 2m + 1 + 1}}{{36}} \Leftrightarrow 2 = {m^2} + 2m + 2\\ \Leftrightarrow {m^2} + 2m = 0 \Leftrightarrow m\left( {m + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 0\\m + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = - 2\end{array} \right.\,\,\,\left( {tmdk} \right)\end{array}\) Vậy \(m \in \left\{ {0; - 2} \right\}\) là giá trị cần tìm. Chọn C. Câu hỏi 37 : Cho đường thẳng \(\left( {{d_1}} \right):y = 2x + 2.\) a) Vẽ đường thẳng \(\left( {{d_1}} \right)\) trên mặt phẳng tọa độ \(Oxy.\) b) Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right):y = x - 3.\) c) Cho đường thẳng \(\left( {{d_3}} \right):y = mx + 5.\) Tìm giá trị của \(m\) để ba đường thẳng \(\left( {{d_1}} \right),\,\left( {{d_2}} \right),\,\left( {{d_3}} \right)\) cắt nhau tại một điểm.
Đáp án: B Phương pháp giải: a) Đồ thị hàm số \(y = ax + b\,\left( {a \ne 0} \right)\) là đường thẳng đi qua hai điểm có tọa độ \(\left( { - \frac{b}{a};0} \right)\) và \(\left( {0;b} \right)\) b) Giải phương trình hoành độ giao điểm để tìm \(x\), từ đó thay trở lại hàm số để tìm tung độ giao điểm\(y.\) c) Tìm điều kiện để ba đường thẳng cắt nhau. Thay tọa độ giao điểm vừa tìm được ở câu \(b\) vào hàm số \(y = mx + 5\) ta tìm được \(m.\) Lời giải chi tiết: Cho đường thẳng \(\left( {{d_1}} \right):y = 2x + 2\) a) Vẽ đường thẳng \(\left( {{d_1}} \right)\) trên mặt phẳng tọa độ \(Oxy.\) Cho \(x = 0 \Rightarrow y = 2\) \(y = 0 \Rightarrow x = - 1\) Đồ thị hàm số \(y = 2x + 2\) là đường thẳng đi qua hai điểm có tọa độ \(\left( {0;2} \right)\)và \(\left( { - 1;0} \right)\) b) Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right):y = x - 3.\) Xét phương trình hoành độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) ta có: \(\begin{array}{l}\,\,\,\,\,\,\,2x + 2 = x - 3\\ \Leftrightarrow 2x - x = - 3 - 2\\ \Leftrightarrow x = - 5\end{array}\) Thay \(x = - 5\) vào hàm số \(y = x - 3\) ta được \(y = - 5 - 3 = - 8\) Vậy tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là \(\left( { - 5; - 8} \right)\). c) Cho đường thẳng \(\left( {{d_3}} \right):y = mx + 5.\) Tìm giá trị của \(m\) để ba đường thẳng \(\left( {{d_1}} \right),\left( {{d_2}} \right),\,\left( {{d_3}} \right)\) cắt nhau tại một điểm. Để ba đường thẳng \(\left( {{d_1}} \right),\left( {{d_2}} \right),\left( {{d_3}} \right)\) cắt nhau thì \(m \ne \left\{ {1;2} \right\}\) Theo câu b) ta có tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là \(\left( { - 5; - 8} \right)\). Để ba đường thẳng \(\left( {{d_1}} \right),\left( {{d_2}} \right),\left( {{d_3}} \right)\) đồng quy thì điểm có tọa độ \(\left( { - 5; - 8} \right)\) cũng thuộc đường thẳng \(\left( {{d_3}} \right).\) Thay \(x = - 5;y = - 8\) vào hàm số \(y = mx + 5\) ta được: \( - 8 = m\left( { - 5} \right) + 5 \Leftrightarrow m = \frac{{13}}{5}\) (thỏa mãn) Vậy \(m = \frac{{13}}{5}.\) Chọn B. Câu hỏi 38 : Cho hàm số \(y = \left( {m - 1} \right)x - 4\) có đồ thị là đường thẳng \(\left( d \right)\). a) Tìm \(m\) để đường thẳng \(\left( d \right)\) song song với đường thẳng \(y = 2x + 5\). b) Vẽ đồ thị hàm số trên với \(m\) tìm được ở câu a. c) Đường thẳng \(\left( d \right)\) cắt trục \(Ox\) tại \(A\), cắt trục \(Oy\) tại \(B\). Tìm \(m\) để tam giác \(OAB\) vuông cân.
Đáp án: C Phương pháp giải: a) Đường thẳng \(d//d' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\). b) Cho lần lượt \(x = 0,y = 0\) tìm tọa độ các điểm đi qua và vẽ đồ thị. c) Tìm tọa độ \(A,B\). Để \(\Delta OAB\) vuông cân tại\(O\)\( \Rightarrow OA = OB\) Lời giải chi tiết: a) Tìm \(m\) để đường thẳng \(\left( d \right)\) song song với đường thẳng \(y = 2x + 5\). Đường thẳng \(\left( d \right)\) song song với đường thẳng \(y = 2x + 5\) \( \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m - 1 = 2\\ - 4 \ne 5\end{array} \right. \Leftrightarrow m = 3\). Vậy \(m = 3\) thì thỏa mãn bài toán. b) Vẽ đồ thị hàm số trên với \(m\) tìm được ở câu a. Với \(m = 3\), ta có : \(\left( d \right):\,\,y = 2x - 4\). Cho \(x = 0\) ta được \(y = 2.0 - 4 = - 4\) nên \(M\left( {0; - 4} \right)\). Cho \(y = 0 \Rightarrow 0 = 2x - 4 \Leftrightarrow x = 2\) nên \(N\left( {2;0} \right)\). Đồ thị hàm số là đường thẳng \(\left( d \right)\) đi qua hai điểm \(\left( {0; - 4} \right)\) và \(\left( {2;0} \right)\) c) Đường thẳng \(\left( d \right)\) cắt trục \(Ox\) tại \(A\), cắt trục \(Oy\) tại \(B\). Tìm \(m\) để tam giác \(OAB\) vuông cân. \(\left( d \right)\) cắt hai trục \(Ox;Oy\) tại \(A,\,\,B\) thì \(m - 1 \ne 0 \Leftrightarrow m \ne 1\). Cho \(x = 0 \Rightarrow y = - 4\)\( \Rightarrow B\left( {0; - 4} \right) \Rightarrow OB = \left| { - 4} \right| = 4\). Cho \(y = 0 \Rightarrow x = \frac{4}{{m - 1}}\)\( \Rightarrow A\left( {\frac{4}{{m - 1}};0} \right) \Rightarrow OA = \frac{4}{{\left| {m - 1} \right|}}\) Để \(\Delta OAB\) vuông cân tại\(O\)\( \Rightarrow OA = OB\) \( \Leftrightarrow \frac{4}{{\left| {m - 1} \right|}} = 4 \Leftrightarrow \left| {m - 1} \right| = 1 \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 2\end{array} \right.\,\,\,\left( {tm} \right)\) Vậy \(m \in \left\{ {0;2} \right\}\). Chọn C. Câu hỏi 39 : Cho hàm số bậc nhất : \(y = \left( {k - 2} \right)x + {k^2} - 2k;\)(\(k\) là tham số) a) Vẽ đồ thị hàm số khi \(k = 1.\) b) Tìm \(k\) để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng \(2.\)
Đáp án: B Phương pháp giải: a) Thay \(k = 1\) vào hàm số rồi vẽ đồ thị hàm số thu được. b) Xác định tọa độ giao điểm. Thay tọa độ đó vào hàm số, từ đó ta tìm được \(m.\) Lời giải chi tiết: a) Vẽ đồ thị hàm số khi \(k = 1.\) Thay \(k = 1\) vào hàm số ta được: \(y = \left( {1 - 2} \right)x + {1^2} - 2.1 \Leftrightarrow y = - x - 1\) Với \(x = 0 \Rightarrow y = - 1\) \(x = - 1 \Rightarrow y = 0\) Đồ thị hàm số \(y = - x - 1\) là đường thẳng đi qua hai điểm có tọa độ \(\left( {0; - 1} \right),\left( { - 1;0} \right)\) Hình vẽ: b) Tìm \(k\) để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng \(2.\) Vì đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng \(2\) nên \(k - 2 \ne 0 \Leftrightarrow k \ne 2\) và tọa độ giao điểm của đồ thị hàm số với trục hoành là \(\left( {2;0} \right)\) Thay \(x = 2;y = 0\) vào hàm số đã cho ta được: \(\begin{array}{l}0 = \left( {k - 2} \right).2 + {k^2} - 2k \Leftrightarrow {k^2} - 4 = 0\\ \Leftrightarrow {k^2} = 4 \Leftrightarrow \left[ \begin{array}{l}k = 2\,\,\,\left( {ktm} \right)\\k = - 2\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\) Vậy \(k = - 2.\) Chọn B. Câu hỏi 40 : Cho hàm số bậc nhất \(y = \left( {m + 1} \right)x + 2\) có đồ thị \(\left( d \right)\) (\(m\) là tham số và \(m \ne - 1\)) a) Vẽ \(\left( d \right)\) khi \(m = 0\). b) Xác định \(m\) để đường thẳng \(\left( d \right)\) song song với đường thẳng \(y = 2x + 1\). c) Xác định \(m\) để \(\left( d \right)\) cắt hai trục \(Ox,Oy\) tại \(A\) và \(B\) sao cho tam giác \(AOB\) có diện tích bằng \(2\) (đơn vị diện tích).
Đáp án: B Phương pháp giải: a) Đường thẳng \(\left( d \right):y = ax + b\,\left( {a \ne 0} \right)\) đi qua hai điểm có tọa độ \(\left( {0;b} \right),\left( { - \frac{b}{a};0} \right).\) b) Hai đường thẳng \(\left( d \right):y = ax + b,\,\left( {d'} \right):y = a'x + b'\) song song với nhau khi \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right..\) c) Tính \(OA,OB \Rightarrow {S_{OAB}} = \frac{1}{2}OA.OB.\) Lời giải chi tiết: a) Khi \(m = 0\) ta có \(\left( d \right):\,y = x + 2\) Với \(x = 0 \Rightarrow y = 2\) \(x = - 2 \Rightarrow y = 0\) Đồ thị hàm số \(y = x + 2\) là đường thẳng \(\left( d \right)\) đi qua hai điểm có tọa độ \(\left( {0;2} \right),\left( { - 2;0} \right)\). Hình vẽ: b) Xác định \(m\) để đường thẳng \(\left( d \right)\) song song với đường thẳng \(y = 2x + 1\). Đường thẳng \(\left( d \right)\) song song với đường thẳng \(y = 2x + 1\) \( \Leftrightarrow \left\{ \begin{array}{l}m + 1 = 2\\2 \ne 1\end{array} \right. \Leftrightarrow m = 1\) Kết hợp điều kiện \(m \ne - 1\) ta có \(m = 1\,\,\left( {tm} \right).\) Vậy \(m = 1\). c) Xác định \(m\) để \(\left( d \right)\) cắt hai trục \(Ox,Oy\) tại \(A\) và \(B\) sao cho tam giác \(AOB\) có diện tích bằng \(2\) (đơn vị diện tích) Do \(m \ne - 1\) nên không mất tính tổng quát ta giả sử \(\left( d \right)\) cắt \(Ox\) và \(Oy\) như hình vẽ Vì \(A\) là giao điểm của \(\left( d \right)\) với \(Ox\) nên \(A\left( {x;0} \right) \Rightarrow \left( {m + 1} \right)x + 2 = 0 \Rightarrow x = - \frac{2}{{m + 1}}\) Suy ra \(A\left( { - \frac{2}{{m + 1}};0} \right) \Rightarrow OA = \frac{2}{{\left| {m + 1} \right|}}\) Vì \(B\) là giao điểm của \(\left( d \right)\) với \(Oy\) nên \(B\left( {0;y} \right) \Rightarrow \left( {m + 1} \right).0 + 2 = y \Rightarrow y = 2\) Suy ra \(B\left( {0;2} \right) \Rightarrow OB = 2\) Vì \(\Delta OAB\) vuông tại \(O\). Khi đó: \({S_{\Delta OAB}} = \frac{1}{2}.OA.OB = \frac{1}{2}.\frac{2}{{\left| {m + 1} \right|}}.2 = \frac{2}{{\left| {m + 1} \right|}}\) Mà \({S_{\Delta OAB}} = 2 \Leftrightarrow \left| {m + 1} \right| = 1\) \( \Leftrightarrow \left[ \begin{array}{l}m + 1 = 1\\m + 1 = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = - 2\end{array} \right.\) (thỏa mãn \(m \ne - 1\)) Vạy \(m = 0\) hoặc \(m = - 2\) thỏa mãn yêu cầu bài toán. Chọn B. Câu hỏi 41 : Cho hàm số \(y = - 0,5x\) có đồ thị là \(\left( {{d_1}} \right)\) và hàm số \(y = x + 2\) có đồ thị là \(\left( {{d_2}} \right)\) a) Vẽ đồ thị \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ \(Oxy.\) b) Xác định hệ số \(a,b\) của đường thẳng \(\left( d \right):y = ax + b\) biết rằng \(\left( d \right)\) song song với \(\left( {{d_1}} \right)\) và \(\left( d \right)\) cắt \(\left( {{d_2}} \right)\) tại một điểm có tung độ là \( - 3\).
Đáp án: C Phương pháp giải: a) Lập bảng giá trị các điểm đi qua của mỗi đồ thị hàm số và vẽ đồ thị. b) Sử dụng \(d//d'\) thì \(a = a',b \ne b'\). Lời giải chi tiết: a) Vẽ đồ thị \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ \(Oxy.\) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ \(Oxy\) Bảng giá trị \(y = - 0,5x\) Bảng giá trị \(y = x + 2\) Đồ thị: b) Xác định hệ số \(a,b\) của đường thẳng \(\left( d \right):y = ax + b\) biết rằng \(\left( d \right)\) song song với \(\left( {{d_1}} \right)\) và \(\left( d \right)\) cắt \(\left( {{d_2}} \right)\) tại một điểm có tung độ là \( - 3\). Vì \(\left( d \right)//\left( {{d_1}} \right)\) nên \(a = - 0,5\) và \(b \ne 0.\) Khi đó \(\left( d \right):y = - 0,5x + b\) Gọi \(A\left( {{x_0}; - 3} \right)\) là tọa độ giao điểm của \(\left( d \right)\) và \(\left( {{d_2}} \right)\) +\(A\left( {{x_0}; - 3} \right) \in \left( {{d_2}} \right)\) \( \Rightarrow - 3 = {x_0} + 2 \Rightarrow {x_0} = - 5\) +\(A\left( { - 5; - 3} \right) \in \left( d \right)\) \( \Rightarrow - 3 = - 0,5.\left( { - 5} \right) + b\) \( \Rightarrow b = - 5,5\) (TMĐK) Vậy \(\left( d \right):y = - 0,5x - 5,5\) Chọn C. Câu hỏi 42 : Cho hai đường thẳng \(\left( d \right):y = \left( {m - 2} \right)x + m\) và \(\left( \Delta \right):y = - 4x + 1\) Câu 1: Tìm \(m\) để \(\left( d \right)\) song song với \(\left( \Delta \right)\).
Đáp án: D Phương pháp giải: Sử dụng điều kiện để hai đường thẳng song song: Hai đường thẳng \(y = ax + b\) và \(y = a'x + b'\) song song với nhau khi và chỉ khi \(a = a',\,\,b \ne b'.\) Lời giải chi tiết: a) Để \(\left( d \right)\) song song với \(\left( \Delta \right)\) thì: \(\left\{ \begin{array}{l}m - 2 = - 4\\m \ne 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}m = - 2\\m \ne 1\end{array} \right. \Rightarrow m = - 2.\) Vậy \(m = - 2\) thỏa mãn yêu cầu. Câu 2: Tìm điểm cố định đường thẳng \(\left( d \right)\) luôn đi qua với mọi \(m\).
Đáp án: B Phương pháp giải: Đưa phương trình về dạng phương trình bậc nhất ẩn \(m\), tìm điều kiện để phương trình có vô số nghiệm, từ đó suy ra tọa độ điểm cố định mà đường thẳng đi qua. Lời giải chi tiết: Ta có: \(\begin{array}{l}y = \left( {m - 2} \right)x + m\\ \Leftrightarrow y = mx - 2x + m\\ \Leftrightarrow \left( {x + 1} \right)m - 2x - y = 0\,\,\,\left( * \right)\end{array}\) Để phương trình (*) nghiệm đúng với mọi \(m\) thì \(\left\{ \begin{array}{l}x + 1 = 0\\ - 2x - y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = 2\end{array} \right.\). Vậy đường thẳng \(\left( d \right)\) luôn đi qua \(A\left( { - 1;2} \right)\) với mọi \(m\). Câu 3: Tìm tọa độ điểm \(B\) thuộc \(\left( \Delta \right)\) sao cho \(AB\) vuông góc với \(\left( \Delta \right)\).
Đáp án: A Phương pháp giải: Sử dụng điều kiện để hai đường thẳng vuông góc: Hai đường thẳng \(y = ax + b\) và \(y = a'x + b'\) vuông góc khi và chỉ khi \(a.a' = - 1\). Tọa độ của giao điểm hai đường thẳng chính là nghiệm của hệ hai phương trình đường thẳng. Lời giải chi tiết: Vì đường thẳng \(AB\) đi qua \(A\left( { - 1;2} \right)\) nên gọi phương trình đường thẳng \(AB\)có hệ số góc \(k\): \(y = k\left( {x + 1} \right) + 2.\) Mà \(AB \bot \left( \Delta \right) = B\) nên suy ra: \(k.\left( { - 4} \right) = - 1\, \Rightarrow k = \dfrac{1}{4}\) Khi đó phương trình đường thẳng \(AB\)là: \(y = \dfrac{1}{4}\left( {x + 1} \right) + 2\) hay \(y = \dfrac{1}{4}x + \dfrac{9}{4}.\) Khi đó tọa độ điểm \(B\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}y = \dfrac{1}{4}x + \dfrac{9}{4}\\y = - 4x + 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = - \dfrac{5}{{17}}\\y = \dfrac{{37}}{{17}}\end{array} \right. \Rightarrow B\left( {\dfrac{{ - 5}}{{17}};\dfrac{{37}}{{17}}} \right)\) Vậy \(B\left( {\dfrac{{ - 5}}{{17}};\dfrac{{37}}{{17}}} \right).\) Câu hỏi 43 : Anh Bình vừa tốt nghiệp loại xuất sắc nên được nhiều công ty mời về làm việc, trong đó có 2 công ty A và B. Để thu hút người tài, cả hai công ty đưa ra hình thức trả lương trong thời gian thử việc như sau: Công ty A: Anh Bình nhận được \(1400\,USD\) ngay khi ký hợp đồng thử việc và mỗi tháng sẽ được trả lương \(1700\,USD.\) Công ty B: Anh Bình nhận được \(2400\,USD\) ngay khi ký hợp đồng thử việc và mỗi tháng sẽ được trả lương \(1500\,USD\) Em hãy tư vấn giúp anh Bình lựa chọn công ty nào để thử việc sao cho tổng số tiền nhận được là lớn nhất. Biết thời gian thử việc của cả hai công ty đều từ 3 tháng đến 8 tháng. Phương pháp giải: Giải bài toán bằng phương pháp đồ thị hàm số bậc nhất. Lời giải chi tiết: Gọi \(x\) (tháng) là số tháng thử việc của anh Bình \(\left( {x \in \mathbb{N}*/3 \le x \le 8} \right)\) Gọi \(y\left( {USD} \right)\) là số tiền anh Bình nhận được sau \(x\) tháng thử việc. Theo công ty A thì số tiền anh Bình nhận được: \(y = 1400 + 1700x\,\,\,\,\,\,\,\left( {{d_1}} \right)\) Theo công ty B thì số tiền anh Bình nhận được: \(y = 2400 + 1500x\,\,\,\,\,\left( {{d_2}} \right)\) Xét phương trình hoành độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\): \(1400 + 1700x = 2400 + 1500x \Leftrightarrow x = 5 \Rightarrow y = 9900\) Xét đồ thị biểu diễn hai hàm \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) như sau: Căn cứ vào đồ thị, ta có thể tư vấn cho anh Bình như sau: +) Nếu thử việc từ 3 đến dưới 5 tháng thì anh Bình nên chọn công ty B sẽ thu được nhiều tiền hơn. +) Nếu thử việc từ hơn 5 tháng đến 8 tháng thì anh Bình nên chọn công ty A sẽ thu được nhiều tiền hơn. +) Nếu thử việc đúng 5 tháng thì anh Bình chọn công ty nào cũng sẽ thu được tiền như nhau. Câu hỏi 44 : Trong mặt phẳng tọa độ \(Oxy,\)cho hai đường thẳng \(\left( {{d_1}} \right):y = {m^2}x - {m^4} + 2\) và \(\left( {{d_2}} \right):y = \frac{{{m^2}}}{{{m^2} + 1}}x + 2\) (\(m\) là tham số thực khác 0). Tìm tất cả giá trị của tham số \(m\) để \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau tại một điểm A duy nhất sao cho diện tích của hình thang \(ABHK\) bằng \(\frac{{15}}{2}.\) Biết \(B\left( { - 1;2} \right)\) và hai điểm \(H,K\) lần lượt là hình chiếu vuông góc của \(B\) và A lên trục hoành.
Đáp án: A Phương pháp giải: Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) theo \(m.\) Lời giải chi tiết: Xét phương trình hoành độ giao điểm của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) là: \(\begin{array}{l}\,\,\,\,\,\,{m^2}x - {m^4} + 2 = \frac{{{m^2}}}{{{m^2} + 1}}x + 2\\ \Leftrightarrow {m^2}\left( {{m^2} + 1} \right)x - {m^2}x = {m^4}\left( {{m^2} + 1} \right)\\ \Leftrightarrow {m^2}x = {m^2}\left( {{m^2} + 1} \right)\\ \Leftrightarrow x = {m^2} + 1\,\,\,\,\,\left( {m \ne 0} \right)\\ \Rightarrow y = {m^2} + 2 \Rightarrow A\left( {{m^2} + 1;{m^2} + 2} \right)\end{array}\) Gọi H, K lần lượt là hình chiếu của B, A lên \(Ox\) nên \(H\left( { - 1;0} \right),K\left( {{m^2} + 1;0} \right)\) \(\begin{array}{l}{S_{ABHK}} = \frac{{15}}{2} \Leftrightarrow \frac{{\left( {AK + BH} \right)HK}}{2} = \frac{{15}}{2}\\ \Leftrightarrow \left( {AK + BH} \right)HK = 15\\ \Leftrightarrow \left( {{m^2} + 4} \right)\left( {{m^2} + 2} \right) = 15\\ \Leftrightarrow {m^4} + 6{m^2} + 8 = 15\\ \Leftrightarrow {m^4} + 6{m^2} - 7 = 0\\ \Leftrightarrow \left( {{m^2} - 1} \right)\left( {{m^2} + 7} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{m^2} - 1 = 0\\{m^2} + 7 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{m^2} = 1 \Rightarrow m = \pm 1\,\,\,\,\left( {tm} \right)\\{m^2} = - 7\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) Vậy \(m = \pm 1.\) Chọn A. Câu hỏi 45 : Hai đường thẳng \(d:\,\,y = mx + m\) và \({d_1}:\,\,y = x + 3m + 2n - mn\) cắt nhau tại điểm \(I\left( {3;9} \right)\). Tính \(m.n\) và \(\dfrac{m}{n}\)
Đáp án: A Phương pháp giải: Vì \(d \cap {d_1} = \left\{ I \right\}\) nên \(\left\{ \begin{array}{l}I \in d\\I \in {d_1}\end{array} \right.\). Thay tọa độ điểm \(I\) vào 2 phương trình đường thẳng \(d,\,\,{d_1}\). Giải hệ phương trình tìm \(m,\,\,n\) và tính \(m.n\), \(\dfrac{m}{n}\). Lời giải chi tiết: Vì \(d \cap {d_1} = \left\{ I \right\}\) nên \(\left\{ \begin{array}{l}I \in d\\I \in {d_1}\end{array} \right.\). \( \Rightarrow \left\{ \begin{array}{l}9 = 3m + m\\9 = 3 + 3m + 2n - mn\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}9 = 4m\\6 = 3m + 2n - mn\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m = \dfrac{9}{4}\\6 = 3.\dfrac{9}{4} + 2n - \dfrac{3}{4}n\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = \dfrac{9}{4}\\6 = \dfrac{{27}}{4} + \dfrac{5}{4}n\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m = \dfrac{9}{4}\\\dfrac{5}{4}n = - \dfrac{3}{4}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = \dfrac{9}{4}\\n = - \dfrac{3}{5}\end{array} \right.\) Vậy \(m.n = \dfrac{9}{4}.\left( { - \dfrac{3}{5}} \right) = \dfrac{{ - 27}}{{20}}\) và \(\dfrac{m}{n} = \dfrac{9}{4}:\left( { - \dfrac{3}{5}} \right) = \dfrac{9}{4}.\left( { - \dfrac{5}{3}} \right) = - \dfrac{{15}}{4}\). Chọn A. Câu hỏi 46 : Biết đường thẳng \(d:y = mx + 4\)cắt \(Ox\) tại\(A\), và cắt \(Oy\) tại \(B\) sao cho diện tích tam giác \(OAB\) bằng\(6\). Khi đó giá trị của \(m\) là:
Đáp án: A Phương pháp giải: Sử dụng kiến thức: - Tìm tọa độ giao điểm của đường thẳng và các trục tọa độ - Giải phương trình chứa dấu giá trị tuyệt đối Lời giải chi tiết: \(\begin{array}{l}d \cap Oy = \left\{ B \right\}\\x = 0 \Rightarrow y = 4\\ \Rightarrow B(0;4) \Rightarrow OB = |4| = 4\\d \cap {\rm{Ox}} = \left\{ A \right\}\\y = 0 \Leftrightarrow mx + 4 = 0 \Leftrightarrow x = \frac{{ - 4}}{m}\left( {m \ne 0} \right)\\ \Rightarrow A\left( {\frac{{ - 4}}{m};0} \right) \Rightarrow OA = \left| {\frac{4}{m}} \right|\end{array}\) \({S_{\Delta AOB}} = \frac{1}{2}OA.OB = 6 \Leftrightarrow \frac{1}{2}.4.\left| {\frac{4}{m}} \right| = 6 \Leftrightarrow |m| = \frac{4}{3} \Leftrightarrow m = \pm \frac{4}{3}.\) Chọn A. Câu hỏi 47 : Điểm cố định mà đường thẳng \(d:y = \frac{{\sqrt k + 1}}{{\sqrt 3 - 1}}x + \sqrt k + 3(k \ge 0)\)luôn đi qua là:
Đáp án: A Phương pháp giải: - \(M\left( {{x_0};{y_0}} \right)\)là điểm cố định mà d luôn đi qua\( \Leftrightarrow M\left( {{x_0};{y_0}} \right) \in d,\forall m \Leftrightarrow m.A + B = 0,\forall m \Leftrightarrow \left\{ \begin{array}{l} A = 0\\ B = 0 \end{array} \right.\) - Giải hệ phương trình tìm nghiệm. Lời giải chi tiết: Gọi \(M\left( {{x_0};{y_0}} \right)\) là điểm cố định mà d luôn đi qua. \(\begin{array}{l} \Leftrightarrow M\left( {{x_0};{y_0}} \right) \in d\begin{array}{*{20}{c}}{}&{}\end{array}\forall k\\ \Leftrightarrow {y_0} = \frac{{\sqrt k + 1}}{{\sqrt 3 - 1}}{x_0} + \sqrt k + \sqrt 3 \begin{array}{*{20}{c}}{}&{}\end{array}\forall k\\ \Leftrightarrow \sqrt k {x_0} + {x_0} + \sqrt {3k} - \sqrt k - \sqrt 3 + 3 - \sqrt 3 {y_0} + {y_0} = 0\begin{array}{*{20}{c}}{}&{}\end{array}\forall k\\ \Leftrightarrow \sqrt k ({x_0} + \sqrt 3 - 1) + {x_0} + 3 - \sqrt 3 + (1 - \sqrt 3 ){y_0} = 0\begin{array}{*{20}{c}}{}&{}\end{array}\forall k\\ \Leftrightarrow \left\{ \begin{array}{l}{x_0} + \sqrt 3 - 1 = 0\\{x_0} + (1 - \sqrt 3 ){y_0} + 3 - \sqrt 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 1 - \sqrt 3 \\(1 - \sqrt 3 ) + (1 - \sqrt 3 ){y_0} + 3 - \sqrt 3 = 0\end{array} \right.\\\Leftrightarrow \left\{ \begin{array}{l}{x_0} = 1 - \sqrt 3 \\(1 - \sqrt 3 ){y_0} + 4 - 2\sqrt 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 1 - \sqrt 3 \\(1 - \sqrt 3 ){y_0} + {(1 - \sqrt 3 )^2} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 1 - \sqrt 3 \\{y_0} = - 1 + \sqrt 3\end{array} \right.\end{array}\) \( \Rightarrow M\left( {1 - \sqrt 3 ;\sqrt 3 - 1} \right)\)là điểm cố định mà d luôn đi qua. Chọn A.
Câu hỏi 48 : Cho đường thẳng \(d:y = ({m^2} - 2m + 2)x + 4\). Tìm \(m\) để \(d\) cắt \(Ox\) tại \(A\) và cắt \(Oy\) tại \(B\) sao cho diện tích tam giác \(AOB\) lớn nhất.
Đáp án: A Phương pháp giải: - Tìm tọa độ giao điểm của đường thẳng và 2 trục tọa độ. - Biện luận và giải phương trình. Lời giải chi tiết: \(\begin{array}{l}d \cap Oy = \left\{ B \right\}\\x = 0 \Rightarrow y = 4 \Rightarrow B(0;4) \Rightarrow OB = |4| = 4\\d \cap {\rm{Ox}} = \left\{ A \right\}\\y = 0 \Leftrightarrow ({m^2} - 2m + 2)x + 4 = 0 \Leftrightarrow x = \frac{{ - 4}}{{{m^2} - 2m + 2}} \Rightarrow A\left( {\frac{{ - 4}}{{{m^2} - 2m + 2}};0} \right) \Rightarrow OA = \left| {\frac{{ - 4}}{{{m^2} - 2m + 2}}} \right|\end{array}\)\({S_{\Delta AOB}} = \frac{1}{2}OA.OB = \frac{1}{2}.4.\left| {\frac{{ - 4}}{{{m^2} - 2m + 2}}} \right| = \frac{8}{{{{(m - 1)}^2} + 1}}\) Ta có \({(m - 1)^2} + 1 \ge 1\begin{array}{*{20}{c}}{}&{\forall m}\end{array}\) Do đó \({S_{\Delta AOB}} = \frac{8}{{{{(m - 1)}^2} + 1}} \le \frac{8}{1} = 8\) Dấu “=” xảy ra khi \(m - 1 = 0 \Leftrightarrow m = 1\). Chọn A. Câu hỏi 49 : Giá trị nguyên có thể có của m để 2 đường thẳng \(d:y = mx - 2;d':y = 2x + 1\) cắt nhau tại điểm có hoành độ là số nguyên.
Đáp án: D Phương pháp giải: - Điều kiện để 2 đường thẳng cắt nhau - Tìm tọa độ giao điểm 2 đường thẳng - Tìm nghiệm nguyên Lời giải chi tiết: Ta có: \(d \cap d' \Leftrightarrow m \ne 2\) Xét phương trình hoành độ giao điểm của d và d’ : \(mx - 2 = 2x + 1 \Leftrightarrow (m - 2)x = 3 \Leftrightarrow x = {3 \over {m - 2}}\) Ta có \(x = {3 \over {m - 2}} \in Z \Leftrightarrow m - 2 \in U(3) = \left\{ { \pm 1; \pm 3} \right\}\) Ta có bảng sau: Vậy \(m \in \left\{ { - 1;1;3;5} \right\}\) Chọn D.
Câu hỏi 50 : Tìm m để đường thẳng \(d:y = mx + 1\) cắt đường thẳng \(d':y = 2x – 1\) tại 1 điểm thuộc đường phân giác góc phần tư thứ II và thứ IV.
Đáp án: B Phương pháp giải: - Điều kiện để 2 đường thẳng cắt nhau - Tìm tọa độ giao điểm 2 đường thẳng cho trước - Đường phân giác của góc phần tư thứ 2 có phương trình y = - x Lời giải chi tiết: Ta có: \(d \cap d' \Leftrightarrow m \ne 2\) Xét phương trình hoành độ giao điểm của d và d’: \(\eqalign{& mx + 1 = 2x - 1 \Leftrightarrow (m - 2)x = - 2 \cr & \Rightarrow x = {{ - 2} \over {m - 2}} \Rightarrow y = 2.{{ - 2} \over {m - 2}} - 1 = {{ - m - 2} \over {m - 2}}. \cr} \) Phương trình đường phân giác góc phần tư thứ 2 là y = - x Vì d và d’ cắt nhau tại 1 điểm điểm thuộc đường phân giác góc phần tư thứ II và thứ IV nên ta có: \({{ - m - 2} \over {m - 2}} = - {{ - 2} \over {m - 2}} \Leftrightarrow - m - 2 = 2 \Leftrightarrow m = - 4\) (t/m) Vậy m = -4. Chọn B. Quảng cáo
|