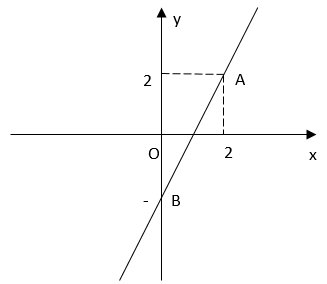
Phương pháp giải:

Phương  pháp:

Câu a: Thay tọa độ của điểm A vào hàm số đã cho để tìm giá trị của m.

Vẽ đồ thị hàm số: Tìm ít nhất hai điểm thuộc đồ thị hàm số sau đó vẽ đường thẳng đi qua hai điểm đó.

Câu b: Đường thẳng \({{d}_{1}}\) căt \({{d}_{2}}\) tai 1 điểm trên trục hoành thì ta có giao điểm là \(M\left( {{x}_{0}};0 \right).\)

Thay điểm M vào phương trình đường thẳng \({{d}_{2}}\) ta được tọa độ điểm M. Sau đó ta thay tọa độ điểm M vào phương trình đường thẳng \({{d}_{1}}\) ta tìm được M.

Lời giải chi tiết:

Giải:

a) Đồ thị hàm số y = 2x +m - 1 đi qua điểm A(2;2) khi và chỉ khi

     2 = 2.2 + m – 1

 \(\Leftrightarrow \)m = -1.

Khi m = -1 hàm số trở thành y = 2x – 2

Cho x = 0 \(\Rightarrow \) y= 2.0 – 2 = -2

Điểm B(0; -2) thuộc đồ thị của hàm số y = 2x - 2

Đồ thị của hàm số y = 2x – 2 là đường thẳng đi qua hai điểm A(2;2) và B(0;-2)

Vẽ đồ thị của hàm số

b) Gọi M là giao điểm của đường thẳng \(y=2x+m-1\) và \(y=x+1.\)

Theo đề bài ta có M thuộc trục hoành \(\Rightarrow M\left( {{x}_{0}};0 \right).\)

M thuộc đường thẳng \(y=x+1\Rightarrow 0={{x}_{0}}+1\Leftrightarrow {{x}_{0}}=-1\Rightarrow M\left( -1;0 \right).\)

M thuộc đường thẳng \(y=2x+m-1\Rightarrow 0=2.\left( -1 \right)+m-1\Leftrightarrow m=3.\)

Vậy với m =  3 thì đồ thị của hàm số y = 2x + m – 1 cắt đồ thị của hàm số y = x +1 tại điểm nằm trên trục hoành.

Phương pháp giải:

- Sử dụng kiến thức được học: Tìm tọa độ giao điểm 2  đường thẳng cho trước

- Điều kiện để 3 đường thẳng đồng quy.

Lời giải chi tiết:

d, d’, d” cắt nhau: \( \Rightarrow \left\{ \begin{array}{l}d \cap d'\\d' \cap d''\\d \cap d''\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m + 2 \ne 2\\2 \ne - 3\\m + 2 \ne - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne - 5\end{array} \right.\)

Xét phương trình hoành độ giao điểm  của (d’)  và(d”) :

\(\matrix{ {2x + 4 =  - 3x - 1} \hfill  \cr { \Leftrightarrow 5x =  - 5} \hfill  \cr { \Leftrightarrow x =  - 1} \hfill  \cr { \Rightarrow y = 2\left( { - 1} \right) + 4 = 2} \hfill  \cr { \Rightarrow A\left( { - 1;2} \right)} \hfill  \cr  } \)

Để (d) ; (d’); (d”) đồng quy thì:

 \(\matrix{{ \Leftrightarrow 2 = \left( {m + 2} \right).\left( { - 1} \right) - 3m} \hfill  \cr  { \Leftrightarrow 2 =  - 2 - 4m} \hfill  \cr { \Leftrightarrow 4m =  - 4} \hfill  \cr { \Leftrightarrow m =  - 1} \hfill  \cr  } \)

Vậy khi m = - 1 thì (d) ; (d’); (d”)   đồng quy tại A(1; -2).

Chọn A.

Phương pháp giải:

Sử dụng kiến thức:

- Viết phương trình đường thẳng đi qua 2 điểm cho trước.

- Giải hệ phương trình tìm nghiệm

- Điều kiện để 3 điểm thẳng hàng.

Lời giải chi tiết:

Gọi \(d:y = {\rm{ax}} + b\) là đường thẳng đi qua A và B.

\(\eqalign{& A(0;3) \in d \Leftrightarrow a.0 + b = 3 \Leftrightarrow b = 3  \cr  & B(2;2) \in d \Leftrightarrow a.2 + b = 2  \cr &  \Rightarrow \left\{ \matrix{b = 3 \hfill \cr 2a + b = 2 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{b = 3 \hfill \cr  a =  - {1 \over 2} \hfill \cr}  \right. \Rightarrow d:y =  - {1 \over 2}x + 3 \cr} \)

Để 3  điểm A, B, C thẳng hàng thì\(C(m + 3;m) \in d:y =  - {1 \over 2}x + 3\)

\( \Leftrightarrow m =  - {1 \over 2}\left( {m + 3} \right) + 3 \Leftrightarrow {3 \over 2}m = {3 \over 2} \Leftrightarrow m = 1\)

Vậy m = 1.

Chọn A.

Phương pháp giải:

Sử dụng kiến thức:

- Hai đường thẳng cắt nhau

- Tìm tọa độ giao điểm hai đường thẳng cho trước

- Điều kiện để 1 điểm thuộc đồ thị hàm số.

Lời giải chi tiết:

 \(\left( d \right):{\rm{ }}y = x + 3;\left( {d'} \right):{\rm{ }}y =  - x + 1;\left( {d''} \right):{\rm{ }}y = \sqrt 3 x - m – 2\) 

 Ba đường thẳng đồng quy \( \Rightarrow \left\{ \begin{array}{l}d \cap d'\\d' \cap d''\\d \cap d''\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 \ne - 1\\- 1 \ne \sqrt 3 \\1 \ne \sqrt 3 \end{array} \right. \Rightarrow m \in R\)

Xét phương trình hoành độ giao điểm của d và d' : \(x + 3 =  - x + 1 \Leftrightarrow 2x =  - 2 \Leftrightarrow x =  - 1 \Rightarrow y = 2\)

Do đó d và d' cắt nhau tại điểm (- 1;2)

Điểm \(A( - 1;2) \in d'':y = \sqrt 3 x - m - 2 \Leftrightarrow 2 = \sqrt 3 .\left( { - 1} \right) - m - 2 \Leftrightarrow m =  - 4 - \sqrt 3 \)

Vậy \(m = - 4 - \sqrt 3 \)

Phương pháp giải:

Sử dụng kiến thức được học:

-          \(M\left( {{x_0};{y_0}} \right)\) là điểm cố định mà d luôn đi qua \( \Leftrightarrow M\left( {{x_0};{y_0}} \right) \in d,\forall m \Leftrightarrow m.A + B = 0,\forall m \Leftrightarrow \left\{ \begin{array}{l}-A = 0\\- B = 0- \end{array} \right.\)

-          Giải hệ phương trình.

Lời giải chi tiết:

Gọi \(M\left( {{x_0};{y_0}} \right)\)là điểm cố định mà d luôn đi qua.

\(\begin{array}{l} \Leftrightarrow M\left( {{x_0};{y_0}} \right) \in d\begin{array}{*{20}{c}}{}&{}\end{array}\forall m\\ \Leftrightarrow 2(m - 1){x_0} + (m - 2){y_0} = 2\begin{array}{*{20}{c}}{}&{}\end{array}\forall m\\ \Leftrightarrow 2m{x_0} - 2{x_0} + m{y_0} - 2{y_0} - 2 = 0\begin{array}{*{20}{c}}{}&{}\end{array}\forall m\\ \Leftrightarrow m(2{x_0} + {y_0}) - 2{x_0} - 2{y_0} - 2 = 0\begin{array}{*{20}{c}}{}&{}\end{array}\forall m\\ \Leftrightarrow \left\{ \begin{array}{l}2{x_0} + {y_0} = 0\\ - 2{x_0} - 2{y_0} - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2{x_0} + {y_0} = 0\\{x_0} + {y_0} =  - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 1\\{y_0} =  - 2\end{array} \right.\end{array}\)

\( \Rightarrow M\left( {1; - 2} \right)\) là điểm cố định mà d luôn đi qua.

Chọn A.

Phương pháp giải:

Sử dụng kiến thức:

-          Tìm tọa độ giao điểm của đường thẳng và các trục tọa độ

-          Giải phương trình chứa dấu giá trị tuyệt đối

Lời giải chi tiết:

\(\begin{array}{l}d \cap Oy = \left\{ B \right\}\\x = 0 \Rightarrow y =  - 1\\ \Rightarrow B(0; - 1) \Rightarrow OB = | - 1| = 1\\d \cap {\rm{Ox}} = \left\{ A \right\}\\y = 0 \Leftrightarrow (2m + 1)x - 1 = 0 \Leftrightarrow x = \frac{1}{{2m + 1}}(m \ne \frac{{ - 1}}{2})\\ \Rightarrow A\left( {\frac{1}{{2m + 1}};0} \right) \Rightarrow OA = \left| {\frac{1}{{2m + 1}}} \right|\end{array}\)

\(\begin{array}{l}{S_{\Delta AOB}} = \frac{1}{2}OA.OB = \frac{1}{2} \Leftrightarrow \frac{1}{2}.1.\left| {\frac{1}{{2m + 1}}} \right| = \frac{1}{2}\\ \Leftrightarrow |2m + 1| = 1 \Leftrightarrow \left[ \begin{array}{l}m = 0\\m =  - 1\end{array} \right.(tmdk)\end{array}\)

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

Bài giải chi tiết:

a) Hàm số biểu diễn số tiền y (nghìn đồng) mà thầy Tưởng phải trả sau x tháng sử dụng dịch vụ internet của công ty FPT là:

\(y = 400 + 50x\)  (nghìn đồng)

Hàm số biểu diễn số tiền y (nghìn đồng) mà thầy Tưởng phải trả sau x tháng sử dụng dịch vụ internet của công ty Viettel là: \(y = 90x\)  (nghìn đồng)

b) Phương trình hoành độ giao điểm của đồ thị hai hàm số là: \(400 + 50x = 90x \Leftrightarrow 400 = 90x - 50x \Leftrightarrow 40x = 400 \Leftrightarrow x = 10\)

Vậy: Vào tháng thứ 10 thì số tiền mà thầy Tưởng phải đóng cho hai công ty là như nhau.

Khi đó, số tiền mà thầy Tưởng  phải trả cho mỗi công ty là: \(y =10.90 = 900\) (nghìn đồng) 

( hoặc \(y = 400 + 50.10 = 900\) (nghìn đồng))

Phương pháp giải:

- Tìm tọa độ giao điểm hai đường thẳng cho trước

- Một điểm nằm trên trục tung khi và chỉ khi hoành độ bằng 0 .

Lời giải chi tiết:

Xét phương trình hoành độ giao điểm của d và d’ :

\( - 4x + m + 1 = {4 \over 3}x + 15 - 3m \Leftrightarrow {{ - 16} \over 3}x = 14 - 4m \Leftrightarrow x = {{3(4m - 14)} \over {16}}\)

d cắt d’  tại điểm nằm trên trục tung \( \Leftrightarrow x = {{3(4m - 14)} \over {16}} = 0 \Leftrightarrow 4m - 14 = 0 \Leftrightarrow m = {7 \over 2}.\)

Chọn D.

Phương pháp giải:

- Tìm tọa độ giao điểm 2 đường thẳng cho trước

- Hoành độ và tung độ giao điểm cùng dấu \( \Leftrightarrow xy > 0\)

Lời giải chi tiết:

Ta có \(d \cap d' \Leftrightarrow m - 3 \ne 2 \Leftrightarrow m \ne 5\)

Xét phương trình hoành độ của d' và d" :

\(\eqalign{& 2x - 1 = (m - 3)x + 2 \Leftrightarrow (m - 5)x =  - 3 \Leftrightarrow x = {{ - 3} \over {m - 5}}  \cr  &  \Rightarrow y = {{ - 6} \over {m - 5}} - 1 = {{ - m - 1} \over {m - 5}} \cr} \)

Theo đề bài:\(x.y > 0 \Leftrightarrow {{ - 3} \over {m - 5}}.{{ - m - 1} \over {m - 5}} > 0 \Leftrightarrow {{3(m + 1)} \over {{{(m - 5)}^2}}} > 0\)

Mà  \({(m - 5)^2} > 0,\forall m \ne 5\)

Suy ra  m > - 1

Kết hợp điều kiện ta có: \(\left\{ \matrix{m > - 1 \hfill \cr m \ne   5 \hfill \cr}  \right.\)

Chọn B. 

Phương pháp giải:

Sử dụng kiến thức:

- Điều kiện để các đường thẳng cắt nhau.

- Tìm tọa độ giao điểm 2 đường thẳng.

- Điều kiện để các đường thẳng đồng quy.

Lời giải chi tiết:

\(\left( d \right):{\rm{ 2}}y + x - 7 = 0 \Leftrightarrow y =  - {1 \over 2}x + {7 \over 2}\)

d, d’, d” cắt nhau: \( \Rightarrow \left\{ \begin{array}{l}d \cap d'\\d' \cap d''\\d \cap d''\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{{ - 1}}{2} \ne 0\\0 \ne m\\\frac{{ - 1}}{2} \ne m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne \frac{{ - 1}}{2}\end{array} \right.\)

Xét phương trình hoành độ giao điểm của (d’) và (d”) : \( - {1 \over 2}x + {7 \over 2} = 3 \Leftrightarrow  - {1 \over 2}x =  - {1 \over 2} \Leftrightarrow x = 1.\)

Để (d); (d’); (d”)  đồng quy thì  \(\left( {1;3} \right) \in \left( {d''} \right) \Leftrightarrow 3 = 1.m - 1 \Leftrightarrow m = 4\)

Kết hợp điều kiện ta có  m = 4 thì (d); (d’); (d”)   đồng quy.

Chọn C.

Phương pháp giải:

Sử dụng kiến thức:

- Tìm tọa độ giao điểm 2 đường thẳng

- Điểm thuộc trục hoành khi và chỉ khi tung độ bằng 0.

Lời giải chi tiết:

Xét phương trình hoành độ giao điểm của d và d’:

\(\eqalign{ & 2x + m + 3 =  - 4x - m - 2 \Leftrightarrow 6x =  - 2m - 5 \Leftrightarrow x = {{ - 2m - 5} \over 6}  \cr &  \Rightarrow y = 2.{{ - 2m - 5} \over 6} + m + 3 = {{m + 4} \over 3} \cr} \)

Ta có d cắt d’  tại điểm thuộc trục hoành nên:\(y = {{m + 4} \over 3} = 0 \Leftrightarrow m =  - 4.\)

Vậy m = - 4

Chọn A.

Phương pháp giải:

Sử dụng kiến thức

- Viết phương trình đường thẳng đi qua 2 điểm cho trước.

- Giải hệ phương trình

- Điều kiện để 3 điểm thẳng hàng.

Lời giải chi tiết:

Gọi \(d:y = {\rm{ax}} + b\) là đường thẳng đi qua A và B.

\(\eqalign{& A(1;2) \in d \Leftrightarrow a.1 + b = 2  \cr & B( - 2;1) \in d \Leftrightarrow a.( - 2) + b = 1 \cr} \)

\( \Rightarrow \left\{ \matrix{ a + b = 2 \hfill \cr   - 2a + b = 1 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{ a = {1 \over 3} \hfill \cr   b = {5 \over 3} \hfill \cr}  \right. \Rightarrow d:y = {1 \over 3}x + {5 \over 3}\)

Để 3 điểm A, B, C thẳng hàng thì  \(D(m;3m - 1) \in d \Leftrightarrow 3m - 1 = {1 \over 3}.m + {5 \over 3} \Leftrightarrow {8 \over 3}m = {8 \over 3} \Leftrightarrow m = 1\)

Vậy m = 1.

Phương pháp giải:

-          Lập bảng xét dấu giá trị tuyệt đối

-          Vẽ đồ thị hàm số với các miền tương ứng

-          Biện luận phương trình dựa vào đồ thị hàm số.

Lời giải chi tiết:

Gọi \(y = |x - 2| - |x - 3|\)

-                               

\(y = \left\{ \begin{array}{l} - (x - 2) - ( - x + 3) =  - 1\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{}&{}\end{array}khi}&{x < 2}\end{array}\\(x - 2) - ( - x + 3) = 2x - 5\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{}&{khi}\end{array}}&{}\end{array}}&{2 \le x \le 3}\end{array}\\(x - 2) - (x - 3) = 1\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{}&{\begin{array}{*{20}{c}}{}&{}\end{array}}\end{array}}&{khi}\end{array}\begin{array}{*{20}{c}}{}&{x > 3}\end{array}\end{array} \right.\)

Phương trình \(|x - 1| - |x + 3| =  - m\) có nghiệm duy nhất

\( \Leftrightarrow \)đường thẳng \(y =  - m\)cắt đồ thị hàm số \(y = |x - 1| - |x + 3|\) tại 1 điểm duy nhất\( \Leftrightarrow  - 1 <  - m < 1 \Leftrightarrow \left\{ \begin{array}{l}m < 1\\m >  - 1\end{array} \right. \Leftrightarrow  - 1 < m < 1\).

Chọn C.

Phương pháp giải:

-          \(M\left( {{x_0};{y_0}} \right)\) là điểm cố định mà d luôn đi qua\( \Leftrightarrow M\left( {{x_0};{y_0}} \right) \in d,\forall m \Leftrightarrow m.A + B = 0,\forall m \Leftrightarrow \left\{ \begin{array}{l}- A = 0\\-B = 0-\end{array} \right.\)

-          Giải hệ phương trình tìm nghiệm.

Lời giải chi tiết:

Gọi \(M\left( {{x_0};{y_0}} \right)\) là điểm cố định mà d luôn đi qua.

\(\begin{array}{l} \Leftrightarrow M\left( {{x_0};{y_0}} \right) \in d\begin{array}{*{20}{c}}{}&{}\end{array}\forall m\\ \Leftrightarrow (m + 2){x_0} + m - 3 = {y_0}\begin{array}{*{20}{c}}{}&{}\end{array}\forall m\\ \Leftrightarrow m{x_0} + 2{x_0} + m - {y_0} - 3 = 0\begin{array}{*{20}{c}}{}&{}\end{array}\forall m\\ \Leftrightarrow m({x_0} + 1) + 2{x_0} - {y_0} - 3 = 0,\forall m\\ \Leftrightarrow \left\{ \begin{array}{l}{x_0} + 1 = 0\\2{x_0} - {y_0} - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} =  - 1\\2.( - 1) - {y_0} = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} =  - 1\\{y_0} =  - 5\end{array} \right. \Rightarrow M( - 1; - 5)\\ \Rightarrow {x_0} + {y_0} =  - 1 + ( - 5) =  - 6.\end{array}\)

Chọn A. 

Phương pháp giải:

Sử dụng kiến thức:

-          Vẽ đồ thị hàm số với các miền tương ứng

-          Biện luận phương trình dựa vào đồ thị hàm số.

Lời giải chi tiết:

Đặt \(y = |2x + 1|\)

Ta có: \(y = |2x + 1| = \left\{ \begin{array}{l}2x + 1\begin{array}{*{20}{c}}{}&{\begin{array}{*{20}{c}}{khi}&{x \ge \frac{{ - 1}}{2}}\end{array}}\end{array}\\ - 2x - 1\begin{array}{*{20}{c}}{}&{khi\begin{array}{*{20}{c}}{}&{x < \frac{{ - 1}}{2}}\end{array}}\end{array}\end{array} \right.\)

Phương trình \(|2x + 1| = m\) vô nghiệm

 \( \Leftrightarrow \)đường thẳng y = m không cắt đồ thị hàm số \(y = |2x + 1| \Leftrightarrow m < 0.\)

Chọn C.

Phương pháp giải:

Sử dụng kiến thức:

-          \(M\left( {{x_0};{y_0}} \right)\) là điểm cố định mà d luôn đi qua\( \Leftrightarrow M\left( {{x_0};{y_0}} \right) \in d,\forall m\Leftrightarrow m.A + B = 0,\forall m \Leftrightarrow \left\{ \begin{array}{l}- A = 0\\- B = 0-\end{array} \right.\)

-          Giải hệ phương trình tìm nghiệm.

Lời giải chi tiết:

\(M\left( {{x_0};{y_0}} \right)\) là điểm cố định mà d luôn đi qua.

\(\begin{array}{l} \Leftrightarrow M\left( {{x_0};{y_0}} \right) \in d\begin{array}{*{20}{c}}{}&{}\end{array}\forall m\\ \Leftrightarrow {y_0} = 3(m + 1){x_0} - 3m - 2\begin{array}{*{20}{c}}{}&{}\end{array}\forall m\\ \Leftrightarrow 3m{x_0} + 3{x_0} - 3m - {y_0} - 2 = 0\begin{array}{*{20}{c}}{}&{}\end{array}\forall m\\ \Leftrightarrow 3m({x_0} - 1) + 3{x_0} - {y_0} - 2 = 0\\ \Leftrightarrow \left\{ \begin{array}{l}{x_0} - 1 = 0\\3{x_0} - {y_0} - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 1\\3.1 - {y_0} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 1\\{y_0} = 1\end{array} \right. \Rightarrow M(1;1)\\ \Rightarrow {x_0}.{y_0} = 1.1 = 1.\end{array}\)

Chọn A.

Phương pháp giải:

Sử dụng kiến thức

-          Tìm tọa độ giao điểm của đường thẳng và các trục tọa độ

-          Giải phương trình chứa dấu giá trị tuyệt đối

Lời giải chi tiết:

\(\begin{array}{l}d \cap Oy = \left\{ B \right\}\\x = 0 \Rightarrow y =  - 1\\ \Rightarrow B(0; - 1) \Rightarrow OB = | - 1| = 1\\d \cap {\rm{Ox}} = \left\{ A \right\}\\y = 0 \Leftrightarrow (k - 2)x - 1 = 0 \Leftrightarrow x = \frac{1}{{k - 2}}(k \ne 2)\\ \Rightarrow A\left( {\frac{1}{{k - 2}};0} \right) \Rightarrow OA = \left| {\frac{1}{{k - 2}}} \right|\end{array}\)

\(\begin{array}{l}{S_{\Delta AOB}} = \frac{1}{2}OA.OB = 1 \Leftrightarrow \frac{1}{2}.1.\left| {\frac{1}{{k - 2}}} \right| = 1\\\Leftrightarrow |k - 2| = \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l}k = \frac{5}{2}\\k = \frac{3}{2}\end{array} \right.(tmdk)\end{array}\)

Chọn D. 

Phương pháp giải:

Lời giải chi tiết:

a)      Điền số thích hợp vào bảng sau.

b)     Hỏi cường độ dòng điện là bao nhiêu thì nhiệt lượng tỏa ra trên dây dẫn là 800J?  Biết 1J = 0,24 calo.

    \(192 = 12.{I^2} \Leftrightarrow {I^2} = 16 \Leftrightarrow I = 4(A)\left( {Do{\rm{ }}I > 0} \right)\)

Phương pháp giải:

Hai đường thẳng \({d_1}:\;\;y = {a_1}x + {b_1},\;\;{d_2}:\;\;y = {a_2}x + {b_2}\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\)

Lời giải chi tiết:

Hai đường thẳng \({d_1}//{d_2} \Leftrightarrow \left\{ \begin{array}{l}{m^2} + 1 = 2\\m + 2 \ne 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} = 1\\m \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 1\\m =  - 1\end{array} \right.\\m \ne 1\end{array} \right. \Leftrightarrow m =  - 1.\)

Chọn D.

Phương pháp giải:

Phương  pháp:

Câu a: Hàm số \(y=ax+b\) đồng biến khi \(a>0\) và nghịch biến khi \(a<0.\)

Câu b: Chú ý: đường thẳng cắt đồ thị hàm số tại điểm M thuộc trục Ox thì \(M\left( {{x}_{0}};0 \right).\) Khi đó ta thay tọa độ điểm M vào phương trình đường thẳng d để tìm m.

Câu c: Cho đường thẳng \({{d}_{1}}:\,\,y={{a}_{1}}x+{{b}_{1}};\,\,\,{{d}_{2}}:\,\,y={{a}_{2}}x+{{b}_{2}}.\) Khi đó \({{d}_{1}}//{{d}_{2}}\Leftrightarrow \left\{ \begin{align}  & {{a}_{1}}={{a}_{2}} \\  & {{b}_{1}}\ne {{b}_{2}} \\ \end{align} \right..\)

Tính diện tích tam giác OMN, ta vẽ đồ thị hàm số và các điểm. Khi đó: \({{S}_{MON}}=\frac{1}{2}OM.ON.\)

Câu d: Ta tìm giao điểm I của đường thẳng \({{d}_{1}};\,\,{{d}_{2}}\) sau đó thay tọa độ điểm I vào phương trình đườn thẳng d để tìm m.

Lời giải chi tiết:

Giải :

a) Hàm số đồng biến khi \(2m-1>0\Leftrightarrow m>\frac{1}{2}\)

Hàm số nghịch biến khi \(2m-1<0\Leftrightarrow m<\frac{1}{2}\)

b)d đi qua điểm (3; 0) \(\Leftrightarrow 0=3\left( 2m-1 \right)+2-m\Leftrightarrow m=\frac{1}{5}\).

c)

\(d\,\,//\,\,y = x + 3 \Leftrightarrow \left\{ \begin{array}{l}2m - 1 = 1\\2 - m \ne 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 1\\m \ne - 1\end{array} \right. \Leftrightarrow m = 1.\)

\(\Rightarrow d:\,\,\,y = x + 1.\)

Ta có đồ thị hàm số:

Ta có: \(OM=1;\,\,\,ON=\left| -1 \right|=1\Rightarrow {{S}_{OMN}}=\frac{1}{2}OM.ON=\frac{1}{2}.\)

Vậy \({{S}_{OMN}}=\frac{1}{2}\).

d) Gọi I là giao điểm của . Khi đó tọa độ điểm I là nghiệm của hệ phương trình: 

\(\begin{array}{l}\left\{ \begin{array}{l}2x - y + 7 = 0\\x + y - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - y = - 7\\x + y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 2\\y = 3\end{array} \right. \Rightarrow I\left( { - 2;3} \right).\\I \in d \Rightarrow 3 = - 2\left( {2m - 1} \right) + 2 - m\\ \Leftrightarrow 3 = - 4m + 2 + 2 - m\\ \Leftrightarrow 5m = 1 \Leftrightarrow m = \frac{1}{5}.\end{array}\)

Vậy \(m=\frac{1}{5}.\)

Phương pháp giải:

Phương pháp:

Câu 1:

+) Thay giá trị của m đã cho vào hàm số.

+) Tìm ít nhất hai điểm thuộc đồ thị hàm số, sau đó vẽ đường thẳng đi qua hai điểm vừa tìm ta được đồ thị hàm số.

Câu 2:

+) Cho hai đồ thị hàm số: \({{d}_{1}}:\,\,\,y={{a}_{1}}x+{{b}_{1}};\,\,\,{{d}_{2}}:\,\,\,y={{a}_{2}}x+{{b}_{2}}\). Ta có:\({{d}_{1}}//{{d}_{2}}\Leftrightarrow \left\{ \begin{align}  & {{a}_{1}}={{a}_{2}} \\  & {{b}_{1}}\ne {{b}_{2}} \\ \end{align} \right..\)

Câu 3:

+) Khoảng cách từ O đến đường thẳng AB là đường cao OH của tam giác OAB vuông tại O. Sử dụng công thức hệ thức lượng trong tam giác vuông để tính chiều cao của tam giác vuông.

Lời giải chi tiết:

Giải:

1) Vẽ đồ thị hàm số với \(m=2.\)

Khi \(m=2\) ta có hàm số: \(y=x+3.\)

Ta có  bảng giá trị:

Đồ thị hàm số:

2) Ta có đường thẳng (1) song song với đường thẳng 

\(y = 2x + 1 \Leftrightarrow \left\{ \begin{array}{l}m - 1 = 2\\m + 1 \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 3\\m \ne 0\end{array} \right. \Leftrightarrow m = 3.\)

Vậy với \(m=3\) thì đồ thị hàm số (1) song song với đường thẳng \(y=2x+1.\)

3) Ta có khoảng cách từ O đến đường thẳng \(d:\,\,\,y=2x+4\Leftrightarrow 2x-y+4=0\) là \(OH\).

Áp dụng công thức hệ thức lượng trong tam giác vuông OAB có

đường cao OH ta có:

\(\begin{align}&\frac{1}{O{{H}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}=\frac{1}{{{4}^{2}}}+\frac{1}{{{\left( -2 \right)}^{2}}}=\frac{5}{16}\Rightarrow O{{H}^{2}}=\frac{16}{5} \\  & \Rightarrow OH=\frac{4}{\sqrt{5}}=\frac{4\sqrt{5}}{5}. \\ \end{align}\)

Vậy khoảng cách từ O đến đường thẳng \(y=2x+4\)

là \(d=\frac{4\sqrt{5}}{5}\) (đvđd).

Phương pháp giải:

- Điều kiện để 2 đường thẳng cắt nhau

- Tìm tọa độ giao điểm 2 đường thẳng cho trước

- Giải phương trình.

Lời giải chi tiết:

\(\eqalign{& d:x + y = m \Leftrightarrow y =  - x + m;  \cr & d':mx + y = 1 \Leftrightarrow y =  - mx + 1  \cr  & d \cap d' \Leftrightarrow  - m \ne  - 1 \Leftrightarrow m \ne 1 \cr} \)

Xét phương trình hoành độ giao điểm của d và d’:

\(\eqalign{&  - x + m =  - mx + 1 \Leftrightarrow (m - 1)x = 1 - m  \cr &  \Rightarrow x = {{1 - m} \over {m - 1}} =  - 1 \Rightarrow y = 1 + m \cr} \)

Do đó d và d’  cắt nhau tại điểm (- 1; m + 1).

Điểm \(( - 1;m + 1) \in (P):y = {x^2} \Leftrightarrow m + 1 = {( - 1)^2} \Leftrightarrow m = 0\) (t/m).

Vậy m = 0.

Chọn D.

Phương pháp giải:

Sử dụng kiến thức:

- Điều kiện để 2 đường thẳng cắt nhau

- Tìm tọa độ giao điểm hai đường thẳng cho trước

- Điều kiện 3 đường thẳng đồng quy

Lời giải chi tiết:

Ta có: \(\left\{ \begin{array}{l}d \cap d'\\d' \cap d''\\d \cap d''\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}- 1 \ne 1\\1 \ne - a\\- 1 \ne - a\end{array} \right. \Leftrightarrow a \ne \pm 1\)

Xét phương trình hoành độ của d’  và d”: \( - x + 1 = x - 1 \Leftrightarrow  - 2x =  - 2 \Leftrightarrow x = 1 \Rightarrow y = 0\)

Để 3  đường thẳng trên đồng quy thì điểm \((1;0) \in d'' \Leftrightarrow 0 =  - a.1 + {a^3} - {a^2} + 1 \Leftrightarrow {a^3} - {a^2} - a + 1 = 0\)

\( \Leftrightarrow {a^2}\left( {a - 1} \right) - \left( {a - 1} \right) = 0 \Leftrightarrow \left( {a - 1} \right)\left( {{a^2} - 1} \right) = 0 \Leftrightarrow {\left( {a - 1} \right)^2}\left( {a + 1} \right) = 0 \Leftrightarrow a =  \pm 1\) (loại do điều kiện)

Vậy không có số a thỏa mãn.

Chọn B.

Phương pháp giải:

Sử dụng kiến thức:

- Điểm thuộc đường thẳng

- Giải phương trình

Lời giải chi tiết:

Điểm  \(A\left( {2; - 1} \right) \in d:y = ax + b \Leftrightarrow 2a + b =  - 1\)

Điểm \(M \in d':2x + y = 3\) có \(x = 0,5 \Rightarrow 2.0,5 + y = 3 \Leftrightarrow y = 2 \Rightarrow M\left( {{1 \over 2};2} \right)\)

\(M\left( {{1 \over 2};2} \right) \in d \Leftrightarrow {1 \over 2}a + b = 2\)

Do đó  \(\left\{ \matrix{ 2a + b =  - 1 \hfill \cr {1 \over 2}a + b = 2 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{2a + b =  - 1 \hfill \cr 2a + 4b = 8 \hfill \cr}  \right. \Rightarrow 3b = 9 \Leftrightarrow b = 3 \Rightarrow a =  - 2\)

Vậy a = -2.

Chọn D.

Phương pháp giải:

Sử dụng kiến thức:

- Điều kiện để 2 đường thẳng cắt nhau

- Tìm giao điểm 2 đường thẳng

- Điểm thuộc góc phần tư thứ nhất khi và chỉ khi x > 0 và y > 0

Lời giải chi tiết:

\(\eqalign{ & d:mx + 2y = 5 \Rightarrow y = {{ - m} \over 2}x + {5 \over 2}  \cr & d \cap d' \Leftrightarrow  - {m \over 2} \ne  - 2 \Leftrightarrow m \ne 4. \cr} \)

Xét phương trình hoành độ giao điểm của d và d’ :

\({{ - m} \over 2}x + {5 \over 2} =  - 2x + 1 \Leftrightarrow {{4 - m} \over 2}x =  - {3 \over 2} \Leftrightarrow x = {3 \over {m - 4}} \Rightarrow y = {{m - 10} \over {m - 4}}\)

Do d cắt d’  tại điểm nằm ở góc phần tư thứ nhất nên ta có: \(\left\{ \matrix{x > 0 \hfill \cr y > 0 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{{3 \over {m - 4}} > 0 \hfill \cr {{m - 10} \over {m - 4}} > 0 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{m > 4 \hfill \cr  m > 10 \hfill \cr}  \right. \Leftrightarrow m > 10\)

Kết hợp điều kiện suy ra m > 10 thỏa mãn đề bài.

Phương pháp giải:

Sử dụng kiến thức

- Tìm tọa độ giao điểm 2 đường thẳng

- Điểm nằm bên trái trục tung khi và chỉ khi x < 0

Lời giải chi tiết:

Xét phương trình hoành độ giao điểm của d và d’ : \(12x + 5 - m = 3x + m + 3 \Leftrightarrow 9x = 2m - 2 \Leftrightarrow x = {{2m - 2} \over 9}\)

Do d cắt d’ tại điểm nằm bên trái trục tung nên ta có: \(x < 0 \Leftrightarrow {{2m - 2} \over 9} < 0 \Leftrightarrow 2m - 2 < 0 \Leftrightarrow m < 1.\)

Chọn A. 

Phương pháp giải:

Sử dụng kiến thức:

-          \(M\left( {{x_0};{y_0}} \right)\)là điểm cố định mà d luôn đi qua\( \Leftrightarrow M\left( {{x_0};{y_0}} \right) \in d,\forall m \Leftrightarrow m.A + B = 0,\forall m \Leftrightarrow \left\{ \begin{array}{l}- A = 0\\- B = 0-\end{array} \right.\)

-          Giải hệ phương trình tìm nghiệm.

Lời giải chi tiết:

Gọi \(M\left( {{x_0};{y_0}} \right)\)là điểm cố định mà d luôn đi qua.

\(\begin{array}{l} \Leftrightarrow M\left( {{x_0};{y_0}} \right) \in d\begin{array}{*{20}{c}}{}&{}\end{array}\forall m\\ \Leftrightarrow (m + 2){x_0} + (m - 3){y_0} - m + 8 = 0\begin{array}{*{20}{c}}{}&{}\end{array}\forall m\\ \Leftrightarrow m{x_0} + 2{x_0} + m{y_0} - 3{y_0} - m + 8 = 0\begin{array}{*{20}{c}}{}&{}\end{array}\forall m\\ \Leftrightarrow m({x_0} + {y_0} - 1) + 2{x_0} - 3{y_0} + 8 = 0\begin{array}{*{20}{c}}{}&{}\end{array}\forall m\\ \Leftrightarrow \left\{ \begin{array}{l}{x_0} + {y_0} - 1 = 0\\2{x_0} - 3{y_0} + 8 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2{x_0} + 2{y_0} = 2\\2{x_0} - 3{y_0} =  - 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} =  - 1\\{y_0} = 2\end{array} \right. \Rightarrow M( - 1;2)\end{array}\)

Vậy chọn D.

Phương pháp giải:

Sử dụng kiến thức:

- \(M\left( {{x_0};{y_0}} \right)\)là điểm cố định mà d luôn đi qua\( \Leftrightarrow M\left( {{x_0};{y_0}} \right) \in d,\forall m \Leftrightarrow m.A + B = 0,\forall m \Leftrightarrow \left\{ \begin{array}{l}- A = 0\\- B = 0- \end{array} \right.\)

Giải hệ phương trình tìm nghiệm

Lời giải chi tiết:

Gọi \(M\left( {{x_0};{y_0}} \right)\) là điểm cố định mà d luôn đi qua.

\(\begin{array}{l} \Leftrightarrow M\left( {{x_0};{y_0}} \right) \in d\begin{array}{*{20}{c}}{}&{}\end{array}\forall m\\\Leftrightarrow (m + 4){x_0} - m + 6 = {y_0}\begin{array}{*{20}{c}}{}&{}\end{array}\forall m\\ \Leftrightarrow m{x_0} + 4{x_0} - m + 6 - {y_0} = 0\begin{array}{*{20}{c}}{}&{}\end{array}\forall m\\ \Leftrightarrow m({x_0} - 1) + 4{x_0} + 6 - {y_0} = 0\begin{array}{*{20}{c}}{}&{}\end{array}\forall m\\ \Leftrightarrow \left\{ \begin{array}{l}{x_0} - 1 = 0\\4{x_0} - {y_0} + 6 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 1\\4.1 - {y_0} =  - 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 1\\{y_0} = 10\end{array} \right. \Rightarrow M(1;10)\\ \Rightarrow x_0^2y_0^2 = {1.10^2} = 100.\end{array}\)

Chọn B.

Phương pháp giải:

+) Lập bảng giá trị sau đó vẽ đồ thị hàm số.

+) Đường thẳng \(y = {a_1}x + {b_1}\) và \(y = {a_2}x + {b_2}\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\) 

Lời giải chi tiết:

a) Vẽ đồ thị hàm số \(y = 2x + 3.\)

Ta có bảng giá trị:

Vậy đồ thị hàm số \(y = 2x + 3\) là đường thẳng đi qua các điểm \(\left( {0;\;3} \right),\;\;\left( { - 1;\;1} \right).\)

b) Xác định \(m\) để đồ thị của hàm số \(y = 2x + 3\) song song với đồ thị hàm số \(y = \left( {{m^2} - 2m + 2} \right)x + 2m - 1.\)

Đường thẳng  \(y = 2x + 3\) song song với đường thẳng \(y = \left( {{m^2} - 2m + 2} \right)x + 2m - 1 \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 2m + 2 = 2\\2m - 1 \ne 3\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 2m = 0\\2m \ne 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 0\\m = 2\end{array} \right.\\m \ne 2\end{array} \right. \Leftrightarrow m = 0.\)

Vậy \(m = 0\) thỏa mãn yêu cầu bài toán.

Chọn C.

Phương pháp giải:

Hai đường thẳng \(y = {a_1}x + {b_1}\) và \(y = {a_2}x + {b_2}\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\)

Thay tọa độ của điểm \(M\) vào phương trình đường thẳng để tìm \(b.\)

Lời giải chi tiết:

Xác định hệ số \(a\) và \(b\) của hàm số \(y = ax + b\) biết đồ thị của nó là đường thẳng \(\left( d \right)\) song song với đường thẳng \(y =  - 3x + 2019\) và đi qua điểm \(M\left( {2;\,\,1} \right).\)

Ta có: đường thẳng \(\left( d \right):\,\,\,y = ax + b\) song song với đường thẳng \(y =  - 3x + 2019\)

\( \Leftrightarrow \left\{ \begin{array}{l}a =  - 3\\b \ne 2019\end{array} \right. \Rightarrow \left( d \right):\,\,\,y =  - 3x + b\,\,\,\left( {b \ne 2019} \right).\)

Đường thẳng \(\left( d \right):\,\,\,y =  - 3x + b\,\,\left( {b \ne 2019} \right)\) đi qua điểm \(M\left( {2;\,\,1} \right)\) nên thay tọa độ điểm \(M\) vào phương trình đường thẳng \(\left( d \right)\) ta được: \(1 =  - 3.2 + b \Leftrightarrow 1 = b - 6 \Leftrightarrow b = 7\,\,\,\left( {tm} \right).\)

Vậy \(a =  - 3;\,\,b = 7.\)

Chọn A.